自己对这些不是很了解,由于接触到了这个概念,所以自己也尽量摸索清楚,这篇文章可能会存在错误,如果有请指正,谢谢

---

• 设计算法要尽量的提高效率,这里的效率高一般指的是算法的执行时间
• 对于如何度量算法的执行时间,比较容易的想法就是执行N次算法然后计时即可(事后统计)

• 那什么是事后统计方法?

  • 主要是通过设计好的测试程序和数据,利用计算机计时器对不同算法编制的程序的运行时间进行比较,从而确定算法效率的高低
  • 这种方法肯定是有很大的缺陷的 :必须先编制好测试算法的测试程序,如果测试完毕后发现算法不行,那么针对此算法编写的测试程序就会作废,这是相当浪费时间的,并且算法在各种机器上的执行效率是不同的,因为机器的配置不同,会造成测试算法会出来不同的结果
• 事前分析估算方法:在计算机程序编写前,依据统计方法对算法进行估算

• 高级语言编写的程序在计算机上运行所消耗的时间取决于下列因素

  • 算法采用的策略,方案
  • 编译生成的代码质量
  • 问题的输入规模
  • 机器执行指令的速度
• 由上因素可见:抛开计算机硬件的差距,一个程序的运行时间依赖于算法的好坏和问题的输入规模

• 现在我们来观察一下下面的哪种算法的执行效率更高:需求1+2+3..+N

  public void test() { Instant old = Instant.now(); long sum = 0 , n = 100_000_000; //执行一次 for (long i = 0; i <= n; i++) { //执行一次+n次,因为for需要判断所以额外的有一次需要计算 sum += i; //执行n次 } //41000000 res : 5000000050000000 System.out.println(Instant.now().getNano() - old.getNano()+" res : " + sum); }

  public void test() { Instant old = Instant.now(); long sum = 0 , n = 100_000_000;//执行一次 sum = (1 + n) * n / 2; //执行一次 //0 res : 5000000050000000 System.out.println(Instant.now().getNano() - old.getNano()+" res : " + sum); }

• 如上的测试结果,可以说明,算法的重要性,明显下面的算法是比上面的算法的执行效率高的,因为n都是一亿的初始值,那么上面的for循环,需要执行一亿次才可以得到sum,而下面的算法直接一次就可以得到结果,上面测试算法时间的方法是事后统计方法(自己没有学过专门的测试程序的编写,所以上面就是一个简单的计算时间的方法),这个测试结果是在我的电脑上执行出来的,而你的电脑可能会跟我的执行结果相差很大,所以这也是事后统计的弊端

上面的算法:一加到一百你会怎么做?当然是(1+100)+(2+99)...,然而这个算法的优化就是上面第二段代码中的公式:sum = (1 + n) * n / 2 = (1+100)*100/2 = 101*100/2 = 5050,即首尾相加乘元素个数除以2

• 如上代码,第一个算法的执行总次数为:1+1+n+n=2n+2,而第二个算法的执行总次数为:1+1=2次
• 如果我们把循环看做一个整体,忽略头尾判断的开销,那么这两个算法其实就是n和1的差距,这时候我们就会冒出一个问题

为什么2n+2会看成n,而1+1会看成1呢?

• 先看下面这个代码

  int x = 0, sum = 0 , n = 100; for (int i = 1; i <= n; i++) { for (int j = 1; j <=n ; j++) { x ++; sum += x; } }

• 上面的例子中是很简单的嵌套循环,并且循环总次数是十分容易计算的,因为n是100,那么只要外层i加1,内层j就会循环100次,所以循环总次数是100*100=1w次,但是如果n不是一个容易计算的值呢?如果是9999...那么现在你要是计算总的执行次数是很困难的,所以这也就是说明了

研究算法的复杂度,侧重点在于研究算法随着输入规模扩大的增长量的一个抽象,而不是精确的计算总的执行次数

• 不计那些循环索引的递增和循环终止条件,变量声明,打印结果等操作,最终在分析程序的运行时间时,我们只关注算法的实现部分
• 我们可以先看下面的图

• 如上蓝色代表一个常量,只要他确定是多少,他就永远是一条水平线并且不会发生变化
• 如上橙色代表一个递增的值(在本图中),比如123456,所以它的折线是根据给的具体的值在变化,在此图中,一直稳步提升
• 如上灰色代表n*n,刚开始三个线都是起始值1,因为灰色线1*1=1,所以他的起点也是1,但是随着数字加大,他一直往上飙升

函数渐近增长

• 判断:哪个算法更好?

假设输入规模都是n,算法A是2n+3,算法B是3n+1,可以这么理解A:即执行两次n次循环然后在执行三次的运算操作,B:三次n次循环运算然后在执行一次运算操作

• 如下

• 如上我们观察到A1和B1是我们需要比较的两个算法,当N>2的时候,A1执行次数比B1要少了,说明A1的算法比B1更好,如图

• 图表描述:B2与B1算法几乎是重叠的,在图中是分辨不出来的,而且A1和A2算法也几乎重叠
• 如上我们更能直观的观察到,当N=3的位置,折线开始出现不再重叠,图表说明的不止这个问题,说明的是A1比A2算法多加的常量3,在这几乎可以省略,算法B1多加的常量1几乎也可以省略,总结起来就是:我们可以忽略这些加法常数

函数渐近增长:给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n>N,f(n)总是比g(n)大,那么我们说f(n)的渐近增长快于g(n)

• 那么上面是什么意思呢?下面是自己的理解

• 如图,f(n)=2n^2+1,g(n)=2n+1,当我们的输入n=1的时候,f(n)=g(n),这时候我们开始套用上面的结论,他说要n>N,那么如果现在我们将N=1,那么n就最小为2,所以算的当n=2的时候f(n)=9,g(n)=5,依次算下去我们发现f(n)>g(n),所以这时候我们这个现象对应上了上面结论中指出的f(n)总是比g(n)大,所以f(n)的渐近增长快于g(n)
• 继续看例子:算法C:4n+8,算法D:2n^2+1,那个算法更好呢?

• 只从分析C1和D1来看,明显是C1更有优势,下面是折线图

• 我们可以看到C1和C2又发生了重叠,依此我们总结出:哪怕去掉与n相乘的常数,两者的比较结果还是没有多大改变,算法C2的次数随着n增长,还是远小于算法D2.而D1和D2的折线图有较大出入,但是D2去掉与n相乘的常数后依旧不影响与A1比较,所以在这去掉与n相乘的常数的结论也是成立的,也就是说:与最高次项相乘的常数并不重要,可以忽略
• 第三个例子:算法E:2n^2+3n+1,F:2n^3+3n+1

• 从分析来看E1是比F1更具有优势的,如下折线图

• 从上来看,E1和E2发生了重叠,并且我们观察到:最高次项的指数大的,函数随着n的增长,结果也会变得增长的特别的快,n的三次方肯定是比n的二次方要增长快的
• 最后一个测试:G:2n^2,H:3n+1,I:2n^+3n+1,那个算法最优?
• 其实根据前面的结论我们已经大概能够估算出了结果了,那么算法从优到差的排列是:H>G>I了,但是还是用折线图说明一下

• 清楚的看出H是最优的算法

• 这个结果又能说明什么呢?:当n足够大的时候,不涉及次方运算的总是优于次方运算的,并且在n足够大的情况下,G与H基本重合了,这就可以得出一个结论:判断算法的效率的时候,函数中的常数和其他次要项常常可以忽略,而更应该关注主项(最高项)的阶数(主项:n^2,那么n就是主项,阶数就是2)
• 下面是当n足够大的时候的折线图

• 到这你应该清楚了为什么2n+2会看成n,而1+1会看成1了,因为他们虽然省略了一些东西,但是完全不印象估算结果
• 前面是一些为了理解时间复杂度的一些铺垫

算法时间复杂度

• 时间频度:一个算法执行所耗费的时间,从理论上是不能算出来的,必须上机运行测试才能知道.但我们不可能也没有必要对每个算法都上机测试,只需知道哪个算法花费的时间多,哪个算法花费的时间少就可以了.并且一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多.一个算法中的语句执行次数称为语句频度或时间频度.记为T(n).
• 时间复杂度的定义:在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级(根据输入规模n估计执行次数).算法的时间复杂度也就是算法的时间量度,记作"T(n)=O(f(n))",它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称为算法的渐近时间复杂度,也叫作时间复杂度,其中f(n)是问题规模n的某个函数(执行次数==时间)
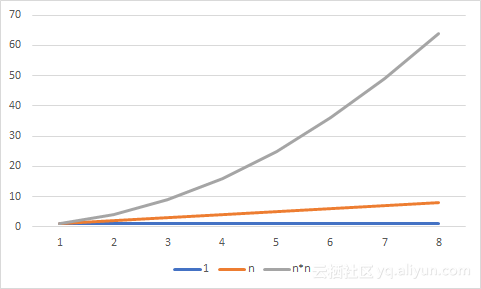
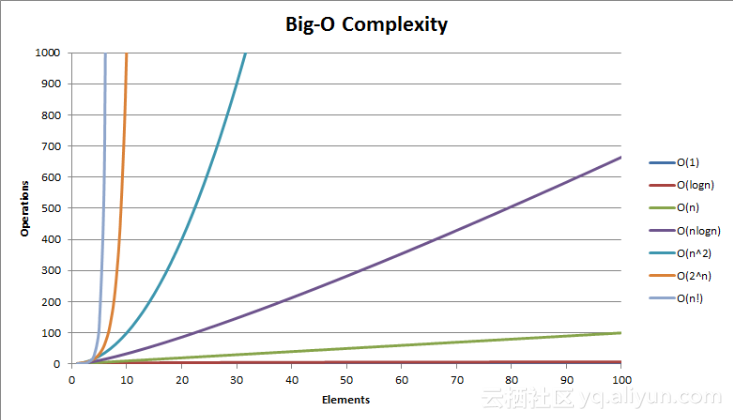
• 这样用大写O()来体现算法时间复杂度的记法,我们称之为大O记法。一般情况下,随着n的增大,T(n)增长最慢的算法为最优算法

• 如何分析一个算法的时间复杂度呢?即推导大O阶攻略

  • 用常数1取代运行时间中的所有加法常数
  • 在修改后的运行次数函数中,只保留最高阶项
  • 如果最高阶项存在且不是1,则去除与这个项相乘的常数
  • 得到的最后结果就是大O阶

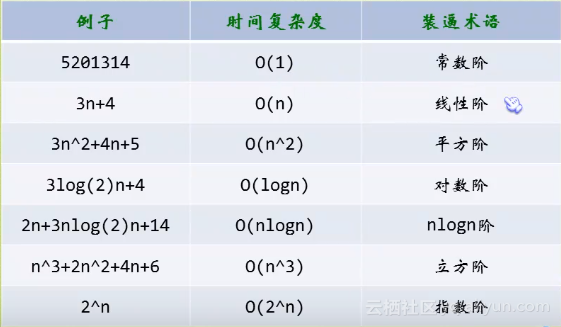
• 例子:常数阶

   long sum = 0 , n = 100_000_000; //1 System.out.println("1"); System.out.println("1"); System.out.println("1"); System.out.println("1"); System.out.println("1"); System.out.println("1"); System.out.println("1"); System.out.println("1"); sum = (1+n) * n / 2; //1

• 根据上面定义的概念:T(n)是关于问题规模n的函数,那么这段代码是也是关于n的一个函数,输出语句并不会因为n的改变而改变,所以直接忽略输出语句,最后记作为O(1),并且上面有说明: 用常数1取代运行时间中的所有加法常数,所以在这段代码中实则是执行次数为1+1=2,用常数1代替加法,那么最后也是O(1)
• 上面有十条语句,有些人想:不应该是O(10)吗?这里需要注意的是,不管你的常数是多少一律写为1,并且在分支结构情况下,分支结构并不会因为n的变化而执行次数增多,所以复杂度也是O(1)

• 例子:线性阶

  long sum = 0 , n = 100_000_000; for (long i = 0; i <= n; i++) { sum += i; }

• 一般含有非嵌套循环涉及线性阶,线性阶就是随着输入规模n的扩大,对应计算次数呈直线增长,在这段代码中,循环随着n的增加而增加,所以它的时间复杂度为O(n)

• 例子:平方阶

  int x = 0, sum = 0 , n = 100; for (int i = 1; i <= n; i++) { for (int j = 1; j <=n ; j++) { sum += 1; } }

• 上面口算得知执行次数为100*100=1w次,而n=100,执行此时就是n^2,所以这的时间复杂度为O(n^2)
• 当然如果有三个嵌套循环,他的时间复杂度就为O(n^3)次方了,所以我们就可以总结出:循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数

• 例子:平方阶

  int x = 0, sum = 0 , n = 100; for (int i = 1; i <= n; i++) { for (int j = i; j <=n ; j++) { sum += 1; } }

• 如上内循环的初始化条件不一样了,它是以外层循环的i的变量的值作为初始值的,他的执行次数计算就为:100+(100-1)+(100-2) = n+(n-1)+(n-2).我们观察这个式子,这不就是本文刚开头的从一加到n的计算方式嘛,所以它也可以用优化算法:n(n+1)/2来计算,n(n+1)/2 = (n^2+n)/2 = n^2/2+n/2,根据之前的攻略,首先没有常数相加,然后看第二条,只保留最高阶项,n^2最高,所以去掉n/2,第三条,去除与最高项相乘的常数,最终得O(n^2)

• 例子:对数阶

  int i = 1 ,n = 100; while (i < n){ i *= 2; }

• 由于每次i*2之后,就离着n更近了,假设有x个2相乘后>=n,则循环退出,于是由2^x=n得到x=log(2)n,所以这个循环的时间复杂度为0(logn)
• 在数学中，log对数是对求幂的逆运算,logA(N)就等于A的多少次方等于N

• 函数调用的时间复杂度分析

  public void test() { int n = 100; for (int i = 0; i < n; i++) { function(i); } } private void function(int i) { System.out.println(i); }

• 如上function函数只有一个输出语句,那么他的时间复杂度是O(1),在test中循环调用function方法,那么function的整体复杂度就为O(n)

• 如果把function改为如下呢?

  private void function(int i) { for (int j = 0; j < i; j++) { System.out.println(j); } }

• 因为在test方法中调用function,function中还有一个循环,所以这的嵌套循环跟上面的第二个平方阶例子相似,所以时间复杂度为O(n^2)

• 例子

  n++; //1 function(n); //n for (int i = 0; i < n ; i++ ) { //n^2 function(i); } for (int i = 0; i < n ; i++ ) { //n^3 for (int j = 0; j < n ; i++ ) { function(j); } }

• 如上代码调用的function函数是前面改动后带循环的function函数,代码中已经表明执行次数,n++一次,直接调用function(n)是执行n次,因为里面就一个根据n的循环,下面第一个for循环中调用function函数,整体构成了一个嵌套for,所以它的执行次数是n^2,再下面是一个三个嵌套for,那么就是n^3,所以总的执行次数为:n^2+n^3+n+1,首先忽略常数,就变为n^2+n^3,然后取最高阶项,那么就是n^3,所以整个时间复杂度为O(n^3)

常见的时间复杂度

• 对应的折线图

• 从上就可以看出在效率上的高低顺序:O(1) 常数阶 < O(logn) 对数阶 < O(n) 线性阶 < O(nlogn) < O(n^2) 平方阶 < O(n^3) < { O(2^n) < O(n!) < O(n^n) }
• 最后三项用大括号把他们括起来是想要告诉大家，如果日后大家设计的算法推导出的“大O阶”是大括号中的这几位，那么趁早放弃这个算法，在去研究新的算法出来吧。因为大括号中的这几位即便是在 n 的规模比较小的情况下仍然要耗费大量的时间，算法的时间复杂度大的离谱，基本上就是“不可用状态”。