0.前言

1.论文概述

Mixtral-8x7B 引爆了MoE的技术方向，更多针对MoE优化的Trick出现，回归模型本身来解析：

1. Mixtral 8x7B 采用了 sMoE模型结构，模型的细节如何？路由负载均衡如何计算？代码如何实现？
2. Mixtral 8x7B 的训练流程和推理流程是怎么样的，如何提高训练和推理效率？
3. Mixtral 8x7B 的模型参数是如何计算的？
4. Mixtral 8x7B 性能硬刚 LLaMA2-70B和 GPT-3.5， 性能一线水准，在 MBPP代码能力超越 3.5

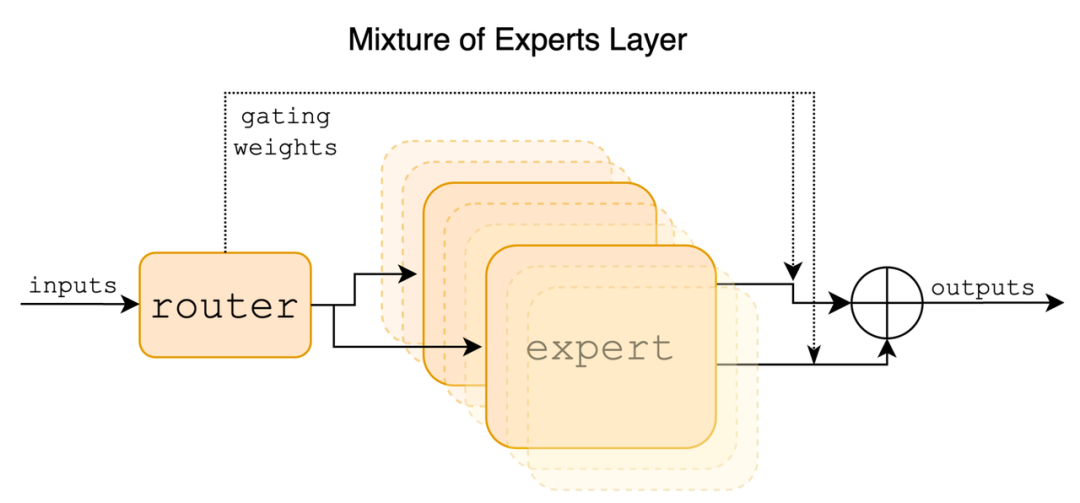
2. Mixtral 8x7B 模型架构和计算流程

Mixtral is based on a transformer architecture [31] and uses the same modifications as described in [18], with the notable exceptions that Mixtral supports a fully dense context length of 32k tokens, and the feed forward blocks are replaced by Mixture-of-Expert layers (Section 2.1). The model architecture parameters are summarized in Table 1.

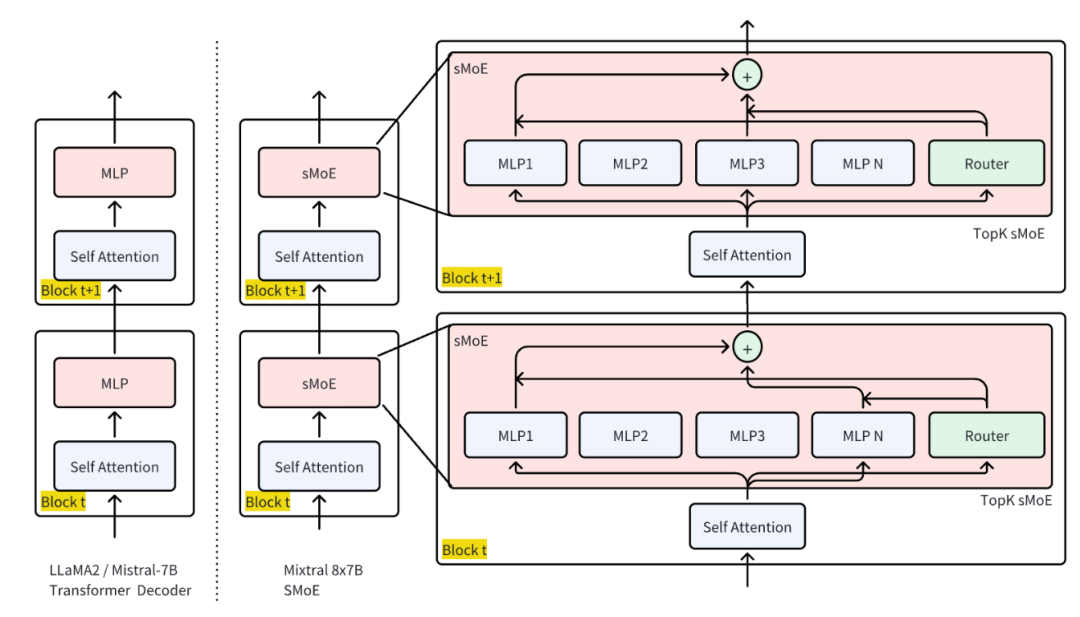
• base的模型结构为 Transformers的改版 Mistral-7B
• MoE 作用在 Feed Forward Blocks上

2.1 Mixtral 模型架构

In a Transformer model, the MoE layer is applied independently per token and replaces the feed-forward (FFN) sub-block of the transformer block. For Mixtral we use the same SwiGLU architecture as the expert function Ei(x) and set K = 2. This means each token is routed to two SwiGLU sub-blocks with different sets of weights. Taking this all together, the output y for an input token x is computed as:

• 以 LLaMA2或 Mistral-7B来说其 MLP都是 SwiGLU形式
• 在 Mixtral-8x7B中 每层的 Decoder层的 MLP都以 sMoE来替换掉

Transformers Mixtral-of-Expert

代码实现:

在Huggingface的Transformers框架中, Mixtral主要有两部分组成

• MixtralDecoderLayer
• MixtralSparseMoeBlock：替换掉原有的MLP层

MixtralForCausalLM(
  (model): MixtralModel(
    (embed_tokens): Embedding(32000, 128)
    (layers): ModuleList(
      (1): MixtralDecoderLayer(
        (self_attn): MixtralAttention(
          (q_proj): Linear(in_features=128, out_features=128, bias=False)
          (k_proj): Linear(in_features=128, out_features=128, bias=False)
          (v_proj): Linear(in_features=128, out_features=128, bias=False)
          (o_proj): Linear(in_features=128, out_features=128, bias=False)
          (rotary_emb): MixtralRotaryEmbedding()
        )
        (block_sparse_moe): MixtralSparseMoeBlock(
          (gate): Linear(in_features=128, out_features=8, bias=False)
          (experts): ModuleList(
            (0-7): 8 x MixtralBLockSparseTop2MLP(
              (w1): Linear(in_features=128, out_features=256, bias=False)
              (w2): Linear(in_features=256, out_features=128, bias=False)
              (w3): Linear(in_features=128, out_features=256, bias=False)
              (act_fn): SiLU()
            )
          )
        )
        (input_layernorm): MixtralRMSNorm()
        (post_attention_layernorm): MixtralRMSNorm()
      )
    )
    (norm): MixtralRMSNorm()
  )

2.2 SMoE 层实现

2.2.1 单个 Expert 实现

import torch
from torch import nn
from transformers import MixtralConfig

class MixtralBLockSparseTop2MLP(nn.Module):
    def __init__(self, config: MixtralConfig):
        super().__init__()
        self.ffn_dim = config.intermediate_size
        self.hidden_dim = config.hidden_size

        self.w1 = nn.Linear(self.hidden_dim, self.ffn_dim, bias=False)
        self.w2 = nn.Linear(self.ffn_dim, self.hidden_dim, bias=False)
        self.w3 = nn.Linear(self.hidden_dim, self.ffn_dim, bias=False)

        self.act_fn = nn.SiLU()

    # Forward 是 SwiGLU
    def forward(self, hidden_states):
        y = self.act_fn(self.w1(hidden_states)) * self.w3(hidden_states)
        y = self.w2(y)
        return y

x = torch.randn(1, 64, 128)
expert = MixtralBLockSparseTop2MLP(config)
print('单个专家为原LLaMA的MLP层')
print(expert)
g = expert(x)
print('单个专家输入:', x.shape)
print('单个专家输出结果：', g.shape)

结果

单个专家为原LLaMA的MLP层
MixtralBLockSparseTop2MLP(
  (w1): Linear(in_features=128, out_features=256, bias=False)
  (w2): Linear(in_features=256, out_features=128, bias=False)
  (w3): Linear(in_features=128, out_features=256, bias=False)
  (act_fn): SiLU()
)
单个专家输入:
torch.Size([1, 64, 128])
单个专家输出结果：
torch.Size([1, 64, 128])

2.2.2 混合Expert实现

class MixtralSparseMoeBlock(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.hidden_dim = config.hidden_size
        self.ffn_dim = config.intermediate_size
        self.num_experts = config.num_local_experts
        self.top_k = config.num_experts_per_tok

        # gating
        self.gate = nn.Linear(self.hidden_dim, self.num_experts, bias=False)

        # 多个 SwiGLU MLP 层组成混合专家
        self.experts = nn.ModuleList([MixtralBLockSparseTop2MLP(config) \
                                      for _ in range(self.num_experts)])

x = torch.randn(1, 64, 128)
experts = MixtralSparseMoeBlock(config)
print('多个专家混合专家')
print(experts)

在以上我们实现了模型的关键结构， 但是这里的sMoE的Forward并没有实现

2.3 SMoE 计算流程

2.3.1 Gating流程

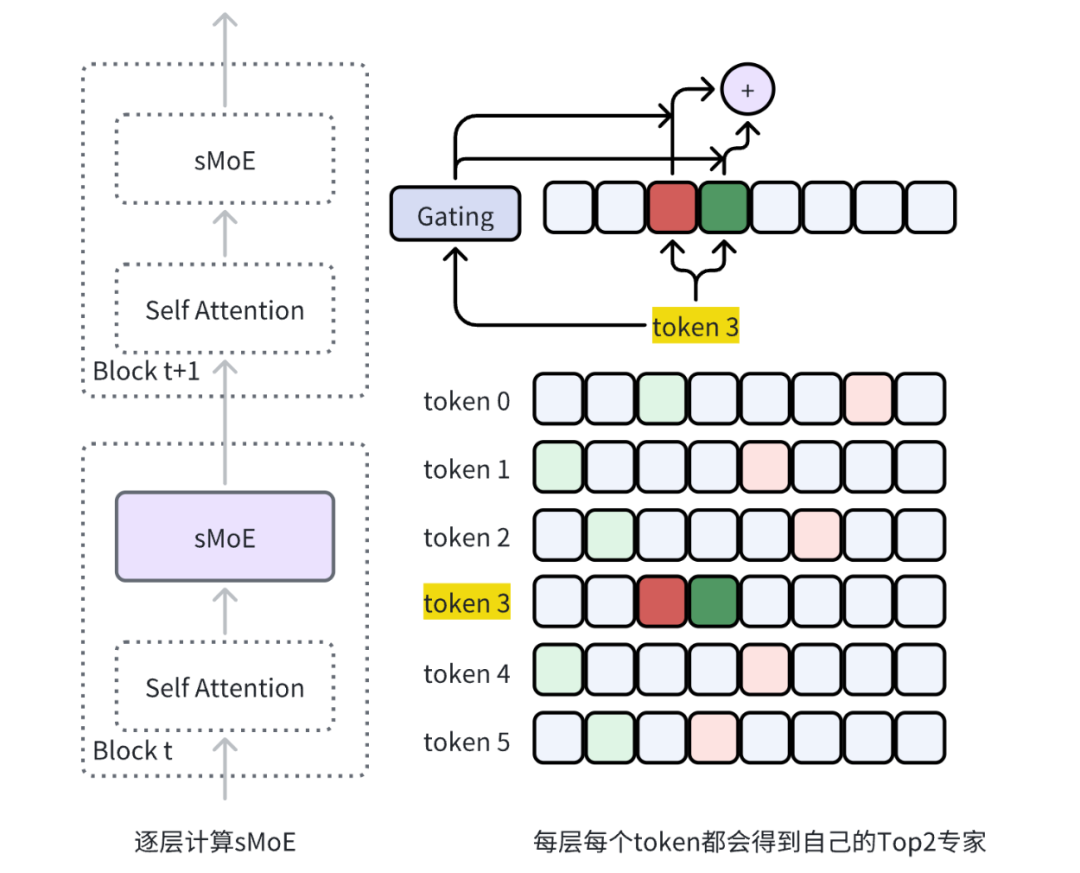
以下表示为多个token的gating计算流程

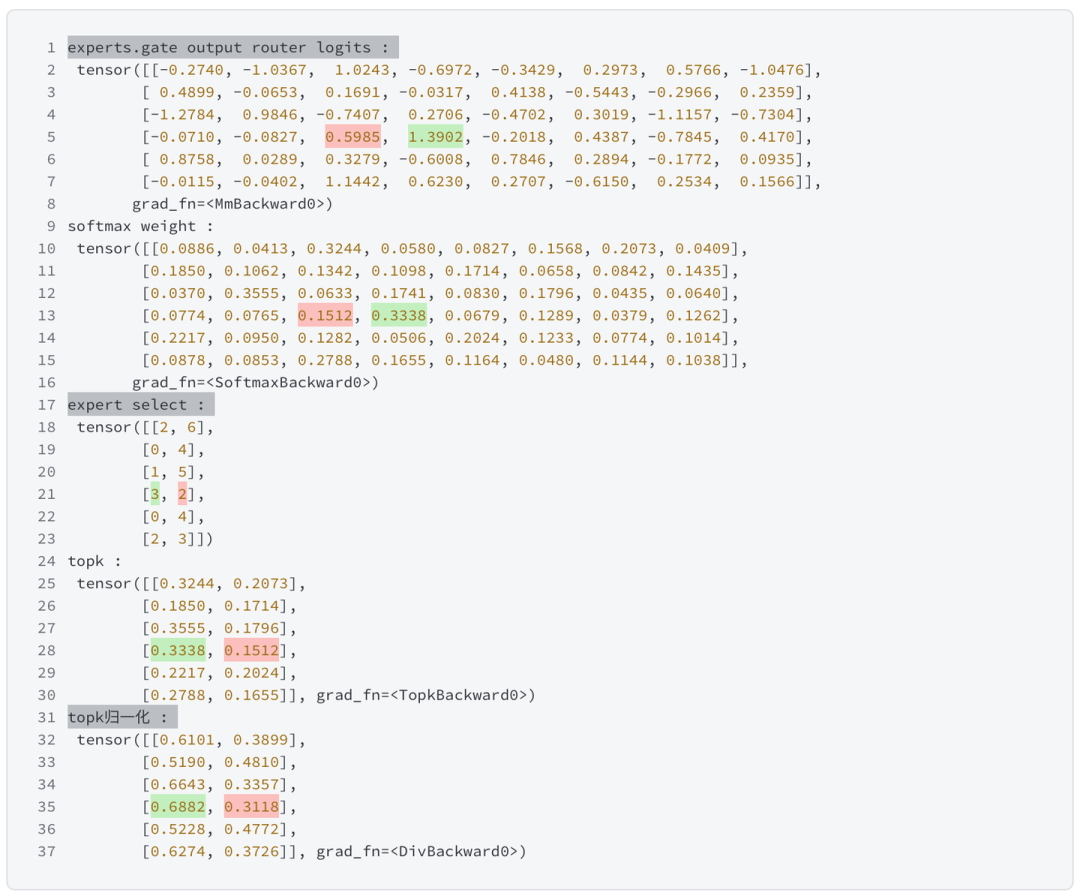
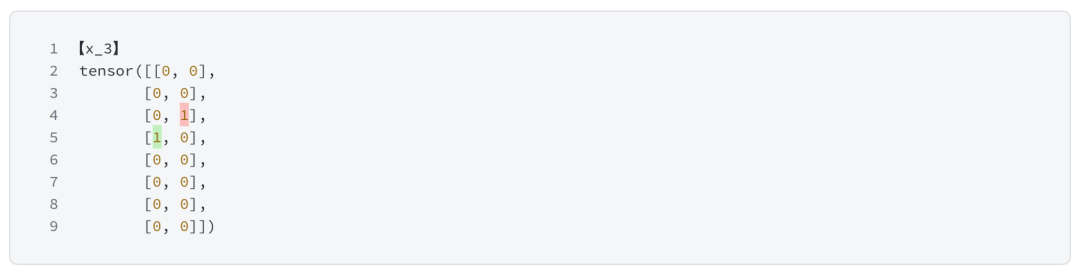
# 阶段一
# 计算稀疏 gating 值
tokens = 6
x = torch.randn(1, tokens, 128) # 6个token
hidden_states = x
batch_size, sequence_length, hidden_dim = hidden_states.shape
hidden_states = hidden_states.view(-1, hidden_dim)

 # 每层都会产生router_logits, 将用于最后作 load balance loss
router_logits = experts.gate(hidden_states)
print(f'experts.gate output router logits : \n {router_logits}')

# 计算 TopK 的 专家 logits 和 Top2 专家的位置
routing_weights = F.softmax(router_logits, dim=1, dtype=torch.float)
print(f'softmax weight  : \n {routing_weights}')

routing_weights, selected_experts = torch.topk(routing_weights, \
                                               experts.top_k, dim=-1)
print(f'expert select : \n {selected_experts}')
print(f'topk : \n {routing_weights}')

routing_weights /= routing_weights.sum(dim=-1, keepdim=True)
print(f'topk归一化 : \n {routing_weights}')

routing_weights = routing_weights.to(hidden_states.dtype)

## One Hot 编码
expert_mask = torch.nn.functional.one_hot(selected_experts, \
                                          num_classes=experts.num_experts).permute(2, 1, 0)
for i in range(tokens):
    print(f'【token_{i}】\n', expert_mask[:,:,i])

追踪x3的结果

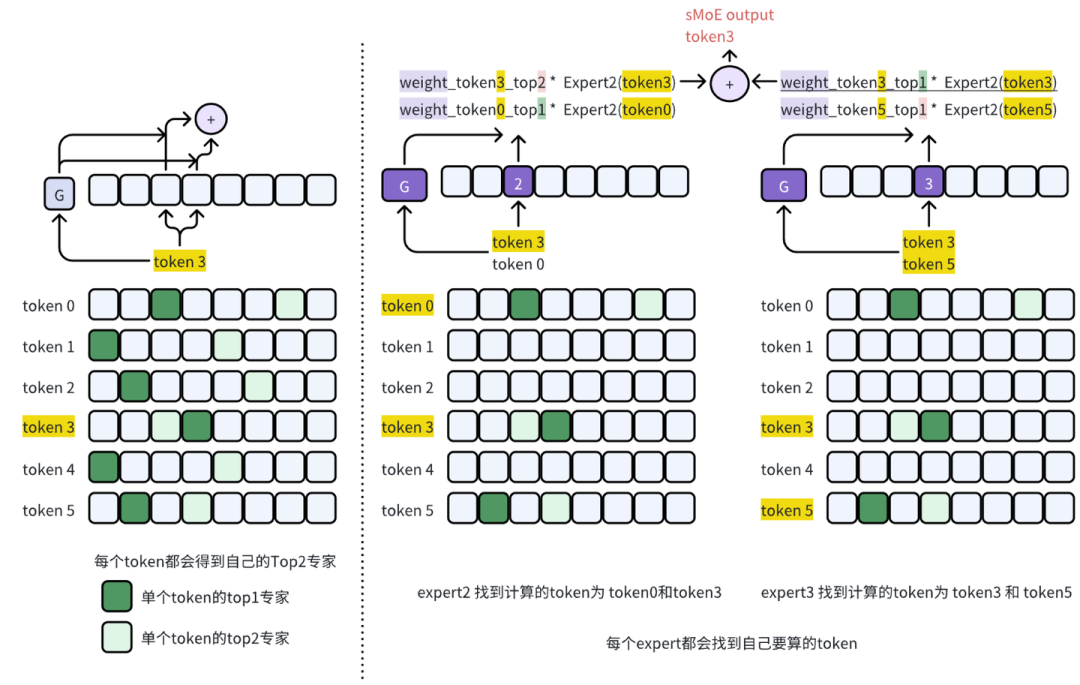
2.3.2 Expert 流程

• sMoE中是基于专家来选择 token来计算的
• token先序：左图为 token3选择 expert 2,  expert 3号来计算 sMoE结果
• expert先序：右图为依次计算 expert2和 expert3才得出 token3 的 sMoE结果

代码实现结果为：

## 最终结果
final_hidden_states = torch.zeros(
    (batch_size * sequence_length, hidden_dim), \
        dtype=hidden_states.dtype, device=hidden_states.device
)
print(f'final moe result shape for each token: {final_hidden_states.shape}')

# 每个专家收集需要计算token
for expert_idx in range(experts.num_experts):

    print(f'--------expert {expert_idx} ---------')

    expert_layer = experts.experts[expert_idx]
    print(expert_mask[expert_idx])
    idx, top_x = torch.where(expert_mask[expert_idx])
    print(f'专家 {expert_idx} 计算的样本编号:',top_x.tolist()) # select x_idx for expert top1
    print(f'专家 {expert_idx} top1:0, top2:1 ',idx.tolist()) # 0 is top1 ,1 is top2
    print(f'有 {len(top_x)} / {x.shape[1]} token 选到专家 {expert_idx}')
    
    top_x_list = top_x.tolist()
    idx_list = idx.tolist()

    current_state = hidden_states[None, top_x_list].reshape(-1, hidden_dim)

    # expert_0(x) * routing_weights
    current_hidden_states = expert_layer(current_state)  \
                            * routing_weights[top_x_list, idx_list, None]

    # 将计算的单个专家结果填入到结果表里
    final_hidden_states.index_add_(0, top_x, current_hidden_states.to(hidden_states.dtype))

    print(current_state.shape) 
    print(routing_weights[top_x_list, idx_list, None].shape)
    print(current_hidden_states.shape)
    print(final_hidden_states.shape)

输出结果为:

2.4 Router Load Balence 计算

路由负载均衡的实现来自Switch Transformers

Computes auxiliary load balancing loss as in Switch Transformer - implemented in Pytorch. See Switch Transformer for more details. This function implements the loss function presented in equations (4) - (6) of the paper. It aims at penalizing cases where the routing between experts is too unbalanced.

2.4.1 Switch Transformers Load Balance Loss

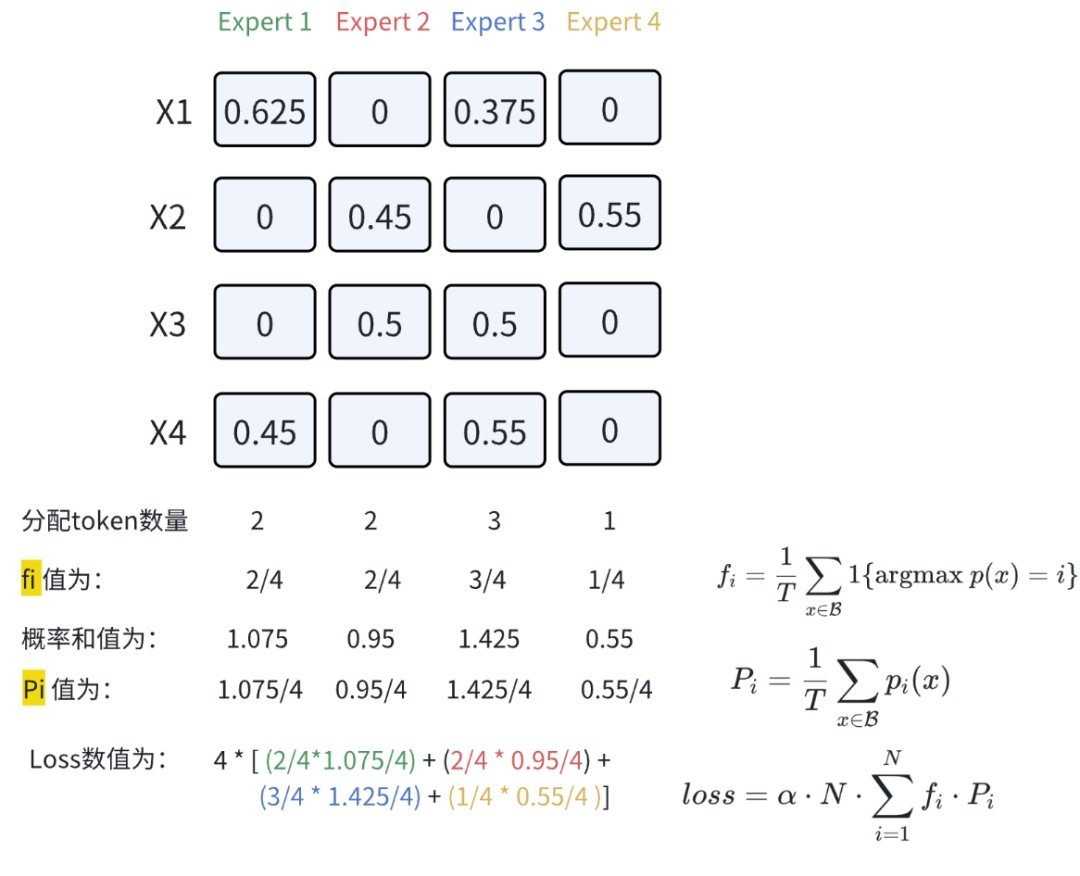
该算法为sMoE简化版load balance , 去除了原版 balance loss 估计

2.4.2 手撕Mixtral Load Balance Loss 计算流程

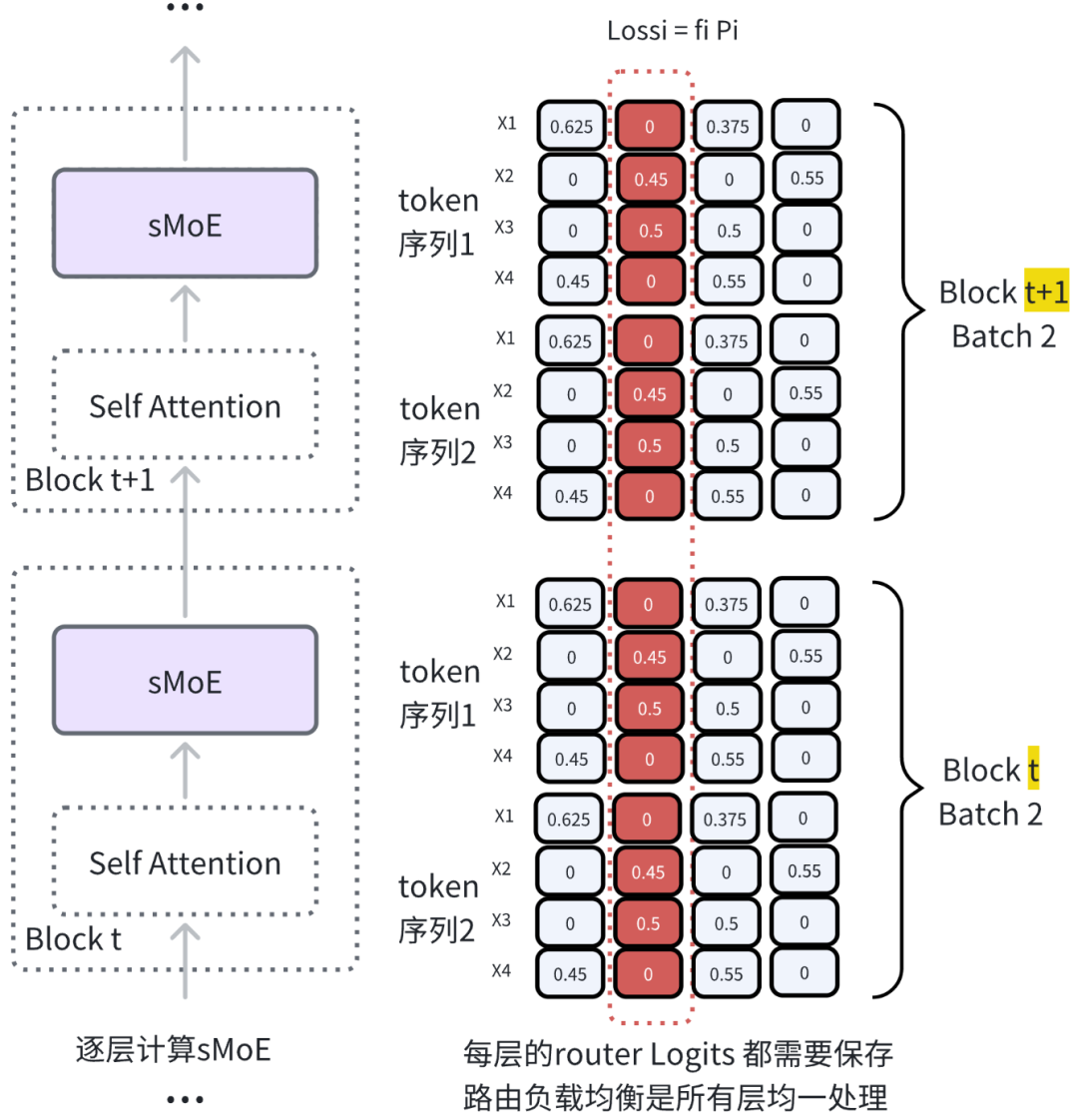
可以想象下layer norm只是在当前层里对所有tokens 做，而负载均衡处理范围更广，对所有层的tokens ，在每个expert的纵向计算出单专家负载值，求和便得到整个网络的负载均衡 loss

2.4.3 手撕Mixtral Load Balance

import torch

num_experts = 8
batch = 10
seq_length = 6
top_k = 2

print(f'sMoE num_experts:{num_experts} top_k:{top_k} batch:{batch} seq_length:{seq_length}')

router_logits_1 = torch.randn(batch, seq_length, num_experts).view(-1,num_experts) # layer 1
router_logits_2 = torch.randn(batch, seq_length, num_experts).view(-1,num_experts) # layer 2
router_logits = [router_logits_1, router_logits_2] 

concatenated_gate_logits = torch.cat(router_logits, dim = 0)
print('单层gating的路由logits:', router_logits_1.shape) 
print('两层gating的路由logits:', concatenated_gate_logits.shape)

print('根据logits top-k 计算热独编码')
routing_weights = torch.nn.functional.softmax(concatenated_gate_logits, dim=-1)
_, selected_experts = torch.topk(routing_weights, top_k, dim=-1)
expert_mask = torch.nn.functional.one_hot(selected_experts, num_experts)
print(expert_mask.shape)

tokens_sum_expert = torch.sum(expert_mask.float(), dim=0)
tokens_per_expert = torch.mean(expert_mask.float(), dim=0)
print(f'top1 每个专家平均处理的token   :', tokens_sum_expert[0])
print(f'top2 每个专家平均处理的token fi:', tokens_per_expert[1])
print(f'top1与top2水平合计', tokens_per_expert.sum(dim=1))

# Compute the average probability of routing to these experts
router_prob_per_expert = torch.mean(routing_weights, dim=0)
print('router_prob_per_expert Pi: ' , router_prob_per_expert)

print( '每个专家的负载：',  tokens_per_expert * router_prob_per_expert.unsqueeze(0))
overall_loss = torch.sum(tokens_per_expert * router_prob_per_expert.unsqueeze(0))
print('final loss:', overall_loss)

计算结果

sMoE num_experts:8 top_k:2 batch:10 seq_length:6
单层gating的路由logits:
torch.Size([60, 8])
两层gating的路由logits:
torch.Size([120, 8])
根据logits top-k 计算热独编码
torch.Size([120, 2, 8])
top1 每个专家平均处理的token   : tensor([10., 14., 19., 17., 14.,  9., 17., 20.])
top2 每个专家平均处理的token fi: tensor([0.1667, 0.1333, 0.1833, 0.0833, 0.1167, 0.1500, 0.0667, 0.1000])
top1与top2水平合计 tensor([1., 1.])
router_prob_per_expert Pi:  tensor([0.1236, 0.1184, 0.1351, 0.1168, 0.1311, 0.1147, 0.1156, 0.1447])
每个专家的负载：tensor([[0.0103, 0.0138, 0.0214, 0.0165, 0.0153, 0.0086, 0.0164, 0.0241],
        [0.0206, 0.0158, 0.0248, 0.0097, 0.0153, 0.0172, 0.0077, 0.0145]])
final loss: tensor(0.2520)

这里的gating logits 是跨batch跨层的，作用在每个token上

3. Mixtral 8x7B 参数量计算

3.1 原论文描述

这里的13B 是指单个 token涉及的模型参数量，实际推理时每个token都有不同的expert ，那么实际运行还是跑47B 参数的, 使用了sMoE 并不会减少显存占用。

3.2 模型参数量计算

忽略GQA计算

dim = 4096
n_layers = 32
head_dim = 128
hidden_dim = 14336
n_heads = 32
n_kv_heads = 8# ignore GQA
vocab_size = 32000
num_experts = 8
top_k_experts = 2

# attention mlp layernorm
llama_num = n_layers * (dim * dim * 4 + hidden_dim * dim * 3 + 2 * dim ) \
        + 2 * vocab_size * dim 
print('llama:', llama_num)

# attention 【mlp*8】 layernorm
moe_num = n_layers * (dim * dim * 4 + hidden_dim * dim * 3 * 8 + 2 * dim ) \
        + 2 * vocab_size * dim 
print('moe:', moe_num)

# attention 【mlp*2】 layernorm
# ToP2-inference
moe_num = n_layers * (dim * dim * 4 + hidden_dim * dim * 3 * 2 + 2 * dim ) \
        + 2 * vocab_size * dim 
print('moe top-2:', moe_num)

结果

llama: 8047034368
moe: 47507046400
moe top-2: 13684178944

4. MoE 扩展

4.1 MegaBlocks

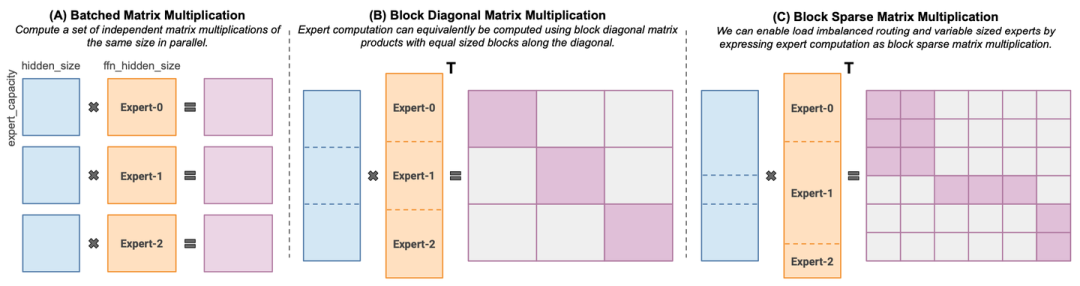
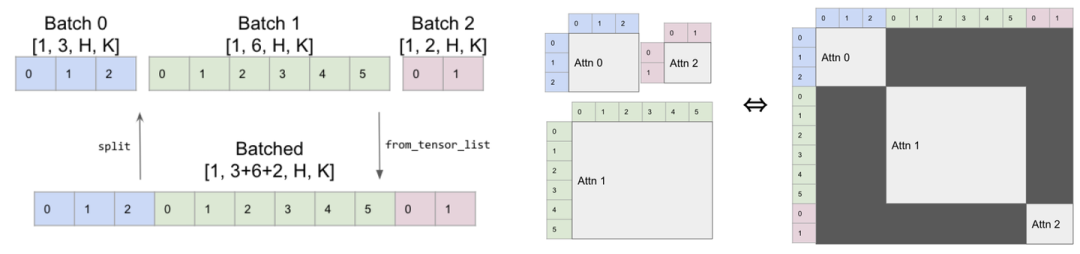
MoE layers can be run efficiently on single GPUs with high performance specialized kernels. For example, Megablocks

MegaBlocks实现稀疏的MoE计算

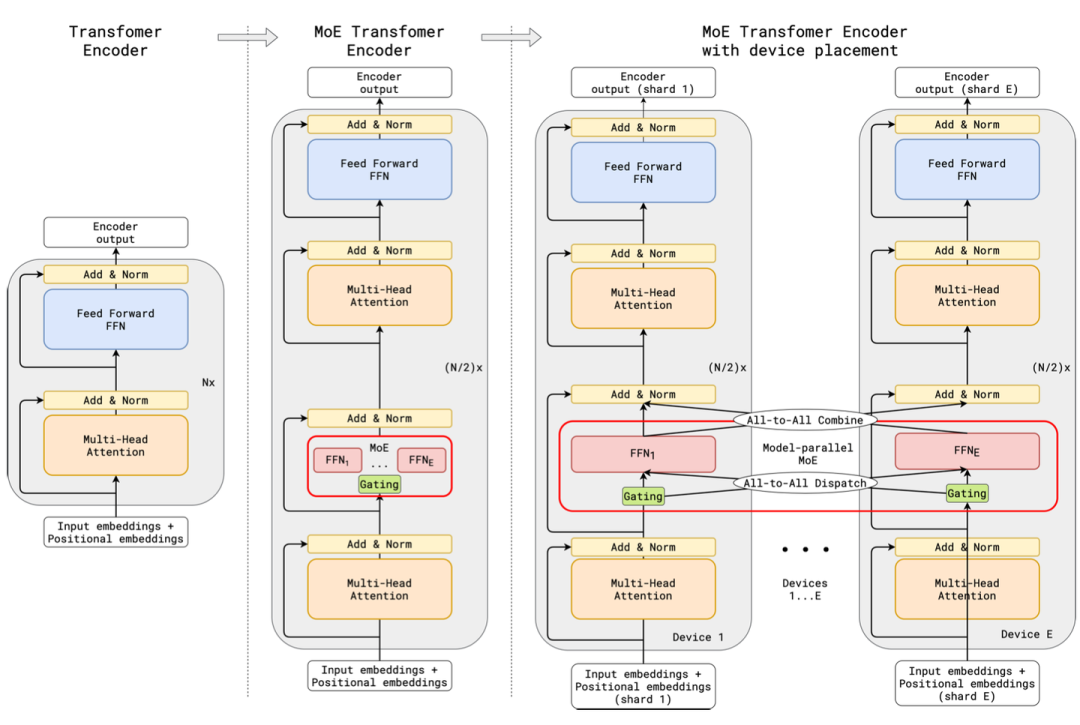
4.2 GShard

Mixtral论文里在load balance里提了一下GShard, 是首篇将MoE引入到Transformers的工作

This formulation is similar to the GShard architecture [21], with the exceptions that we replace all FFN sub-blocks by MoE layers while GShard replaces every other block, and that GShard uses a more elaborate gating strategy for the second expert assigned to each token.

GShard在不同GPU上分配不同的专家，其他参数都共享，数据派发到专家，专家结果汇总都由All-to-All算子实现

DeepSpeed-MoE源码对All-to-All的实现如下

class _AllToAll(torch.autograd.Function):

    @staticmethod
    def forward(
            ctx: Any,
            # TODO: replace with DS process group
            group: torch.distributed.ProcessGroup,
            input: Tensor) -> Tensor:# type: ignore
        ctx.group = group
        input = input.contiguous()
        output = torch.empty_like(input)
        dist.all_to_all_single(output, input, group=group)
        return output

    @staticmethod
    def backward(ctx: Any, *grad_output: Tensor) -> Tuple[None, Tensor]:
        return (None, _AllToAll.apply(ctx.group, *grad_output))
        
class MOELayer(Base):
     # ...
     def forward(self, *input: Tensor, **kwargs: Any) -> Tensor:
        # ...
        dispatched_input = _AllToAll.apply(self.ep_group, dispatched_input)

        # Re-shape after all-to-all: ecm -> gecm
        dispatched_input = dispatched_input.reshape(self.ep_size, self.num_local_experts, -1, d_model)

        expert_output = self.experts(dispatched_input)


        expert_output = _AllToAll.apply(self.ep_group, expert_output)

    #...

4.3 DeepSpeed-MoE

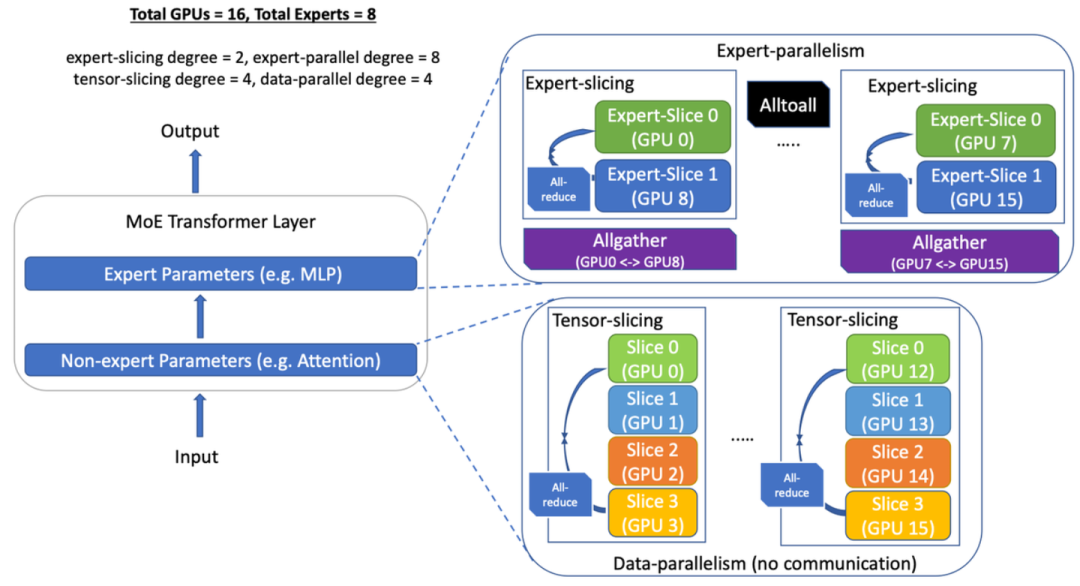
• 更加工程化的实现可以看 DeepSpeed-MoE的开源方案
• MoE层使用 Expert-Paralallelism做并行  AlltoAll实现如上
• 非 MoE层使用 TP+DP

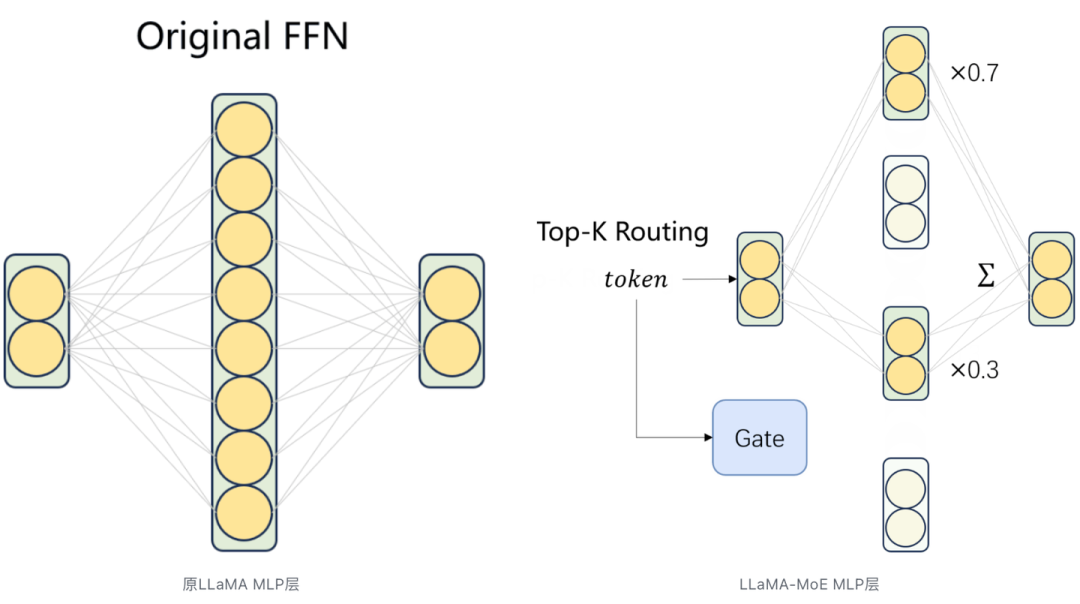
4.4 LLaMA-MoE

Mixtral 8x7B训不动？试试将LLaMA原MLP改造成LLaMA-MoE

LLaMA-MoE 上关键代码是用LinearGLUExperts代替原本LLaMA里的SwiGLU层

 class LinearGLUExperts(nn.Module):
    # ...
    def __init__(...):
        # ... 
        # 每个专家都创建SwiGLU MLP层
        for i in range(num_experts):
            # this matrix will be transposed when performing linear forwarding
            this_expert_weight_gate = nn.Parameter(
                torch.empty((size_experts[i], in_features), **factory_kwargs)
            )
            # this matrix will be transposed when performing linear forwarding
            this_expert_weight_up = nn.Parameter(
                torch.empty((size_experts[i], in_features), **factory_kwargs)
            )
            # this matrix will be transposed when performing linear forwarding
            this_expert_weight_down = nn.Parameter(
                torch.empty((out_features, size_experts[i]), **factory_kwargs)
            )
            self.weight_gate.append(this_expert_weight_gate)
            self.weight_up.append(this_expert_weight_up)
            self.weight_down.append(this_expert_weight_down)
        # ...

5. Mixtral 8x7B 总结 & 进一步阅读

• Mixtral 8x7B实现并不复杂，其中 load-balance loss是 expert-wise维度计算的
• 当前发布的模型还是围绕模型结构展开的， 期待 mistral.AI上线创新的对齐方案
• 涉及到多机多卡的 sMoE分布式训练非常需要工程技巧, 不同的模型架构和集群可以有多种 DP\TP\EP..组合方案，
• 在·Mixtral·中对于实验反直觉论点 专家的知识是作用在  token  级别，而不是domain级别，对 MoE 感兴趣的话可以进一步开盒分析

Reference

1. Mixture of Experts Explained
2. 方佳瑞：MoE训练论文解读之Megablocks：打破动态路由限制
3. 方佳瑞：MoE训练系统之JANUS：参数服务器助力MoE训练
4. 方佳瑞：MoE训练论文解读之Tutel: 动态切换并行策略实现动态路由
5. 西门宇少：对MoE大模型的训练和推理做分布式加速——DeepSpeed-MoE论文速读
6. 吃果冻不吐果冻皮：大模型分布式训练并行技术（八）-MOE并行
7. 孟繁续：Mixtral-8x7B 模型挖坑
8. Mixtral-of-experts
9. Mistral-7B
10. Gshard
11. Switch Transformers
12. sMoE
13. Transformers-Mixtral-of-Experts
14. DeepSpeed-MoE
15. Megablocks
16. LLaMA-MoE

本文由 Hugging Face 中文社区内容共建项目提供，稿件由社区成员投稿，经授权发布于 Hugging Face 公众号。文章内容不代表官方立场，文中介绍的产品和服务等均不构成投资建议。了解更多请关注公众号:

如果你有与开源 AI、Hugging Face 相关的技术和实践分享内容，以及最新的开源 AI 项目发布，希望通过我们分享给更多 AI 从业者和开发者们，请通过下面的链接投稿与我们取得联系: