本博文使用图文描述了平衡二叉搜索树的插入过程:
1: 寻找插入点
2:向上回溯寻找失去平衡的节点 (状态不等于EH的节点)
3:旋转
平衡二叉搜索树
平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。 数值关系,右孩子的值 > 当前节点的值 > 左孩子的值。
平衡二叉搜索树节点的状态
1:左子树比右子树高 LH
2:左子树和右子树一样高 EH
3:右子树比左子树高 RH
![]()
如上图每个节点的状态如下。
![]()
TreeNode 的定义
static final class TreeNode<T> {
TreeStatus treeStatus = TreeStatus.EH;
T value;
TreeNode<T> left;
TreeNode<T> right;
TreeNode<T> parent;
public TreeNode(T value) {
this.value = value;
}
public TreeNode(T value, TreeNode<T> p) {
this.value = value;
this.parent = p;
}
public String toString() {
return "value=" + value.toString();
}
}
搜索插入点
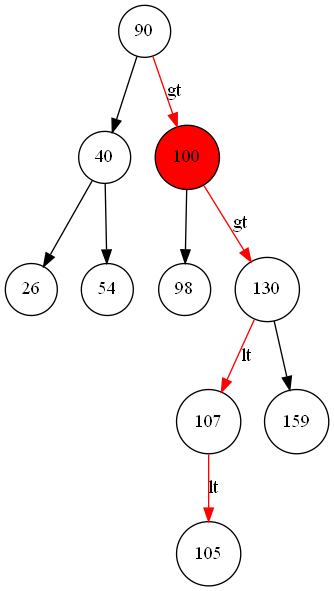
以向平衡二叉树插入105为例。
搜索过程
![]()
105 gt 90 搜索90的右子树
105 gt 100 搜索100的右子树
105 lt 130 搜索130的左子树
105 lt 107 搜索107的左子树
107的左子树为空,停止搜索, 105为107的左孩子。
插入新点节之后搜索途中的节点的状态发生改变,需要回溯更改每个节点的状态。
107节点的状态为EH,105为107的左孩子,所以107的状态更改为LH,
130节点的状态为EH,107为130的左孩子,所以130的状态更改为LH,
100节点的状态为RH, 130 为100的右孩子, 所以 100节点失去平衡。
向上回溯的图解如下。
情况1: 回溯途中所有节点的状态都为EH, 那么树的平衡性不会发生改变。
![]()
直观一点的图。
![]()
向上回溯的路径为:
![]()
在插入54节点之前,所有节点的状态为EH,但是在插入54节点之后。
51 由EH---> RH
55 由EH--->LH
50 由EH---> RH
100 由EH--->LH
![]()
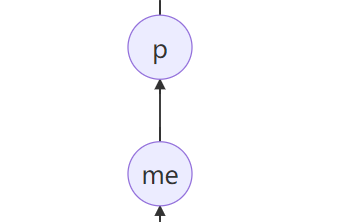
如果me是p的左孩子,那么p的状态改为LH,
如果me是p的右孩子,那么p的状态改为RH。
p=p.parent ;
me=me.parent;
情况2:回溯的途中遇到了第一个状态不为EH的节点,假设该节点为pp。
![]()
由pp,p来决定pp树是否失去平衡。
假设pp的状态为LH,
如果p为pp的左孩子,那么pp树将会失去平衡。 如果p的状态为LH,那么进行LL旋转,如果p的状态为RH,那么进行LR旋转。
如果p为pp的右孩子,那么pp树将维持平衡,并且pp的状态需要修改为EH.
![]()
平衡二叉树有6个插入点:
![]()
当插入点为1或者2时, 引起LL旋转。
当插入点为3或者4时,引起LR旋转。
当插入点为5或者6时,不会引发旋转。
由(pp.treeStatus, p.treeStatus)来决定做那种旋转。。。
镜像的pp的状态为RH;
下面开始讲旋转:
LL 旋转
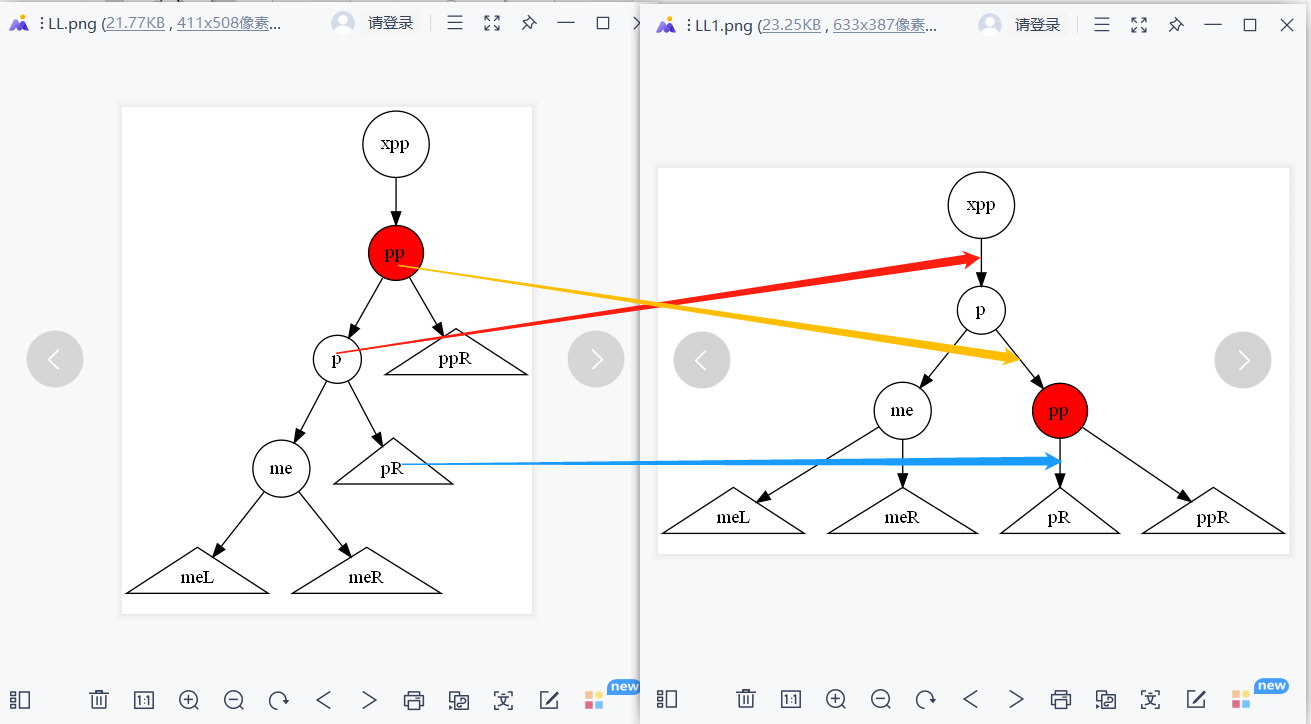
pp为失衡的节点。 p为pp的左孩子,me为p的左孩子, xpp为pp的父节点。
![]()
步骤1: pr = p.right;
步骤2: p.pright = pp; pp.parent = p;
步骤3: pp.left = pr ; pr.parent = pp ;
步骤4: p.parent=xpp , 确定p是xpp的左孩子还是右孩子
重点说明 如果xpp为空,则p节点为新的root节点。
旋转之后 p和pp节点的状态均为EH。
LR旋转
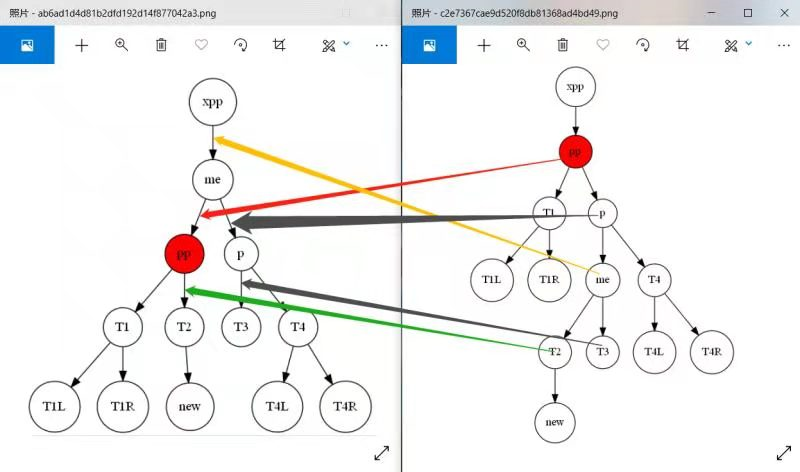
pp为失衡的节点。 p为pp的左孩子,me为p的右孩子, xpp为pp的父节点。
![]()
步骤1 : mel =me.left; mer= me.right
步骤2: me.left = p ; me.right = pp; p.parent = me, pp.parent = me ;
步骤3: p.right = mel ; pp.left = mer ; mel.parent = p ; mer.parent = pp ;
步骤4: me.parent = xpp ; 确定me是xpp的左孩子还是右孩子
重点说明 如果xpp为空,则me节点为新的root节点。
状态的改变:
如果me的状态为LH 那么p的状态为EH , pp的状态为RH;
如果me的状态为RH 那么p的状态为LH, pp的状态为EH ;
如果me的状态为EH 那么p的状态为EH , pp的状态为EH;
旋转完成之后me的状态一定为EH。
RR旋转和LL旋转是镜像关系。
![]()
RL和LR是镜像关系。
![]()
本博文讲述了平衡二叉搜索树的插入过程:
1: 寻找插入点
2:向上回溯寻找失去平衡的点pp (pp,p,me)。 (即向上回溯寻找到状态不等于EH的点)
3:旋转
如果对您理解平衡二叉搜索树有帮助还请帮忙点赞。
如果您发现博文的描述有错误或者漏洞,请发表评论。
转载请注明博文出处。
实现见 https://gitee.com/tuerqidi/avl