前言 在个人的专栏中,其他排序陆陆续续都已经写了,而堆排序迟迟没有写,趁着国庆假期的尾声,把堆排序也写一写。插入类排序—(折半)插入排序、希尔排序
交换类排序—冒泡排序、快速排序手撕图解
归并类排序—归并排序(逆序数问题)
计数排序引发的围观风波——一种O(n)的排序
两分钟搞懂桶排序
对于常见的快排、归并这些O(nlogn)的排序算法,我想大部分人可能很容易搞懂,但是堆排序大部分人可能比较陌生,或许 在Java的comparator接口中可能了解一点。 但堆排序在应用中比如优先队列此类维护动态数据效率比较高,有着非常广泛的应用。
而堆排序可以拆分成堆 和排序 ,其中你可能对堆比较陌生,对排序比较熟悉,下面就带你彻底了解相关内容。
堆 什么是堆?
谈起堆,很多人第一联想到的是土堆,而在数据结构中这种土堆与完全二叉树更像,而堆就是一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树(完全)的数组对象。且总是满足以下规则:
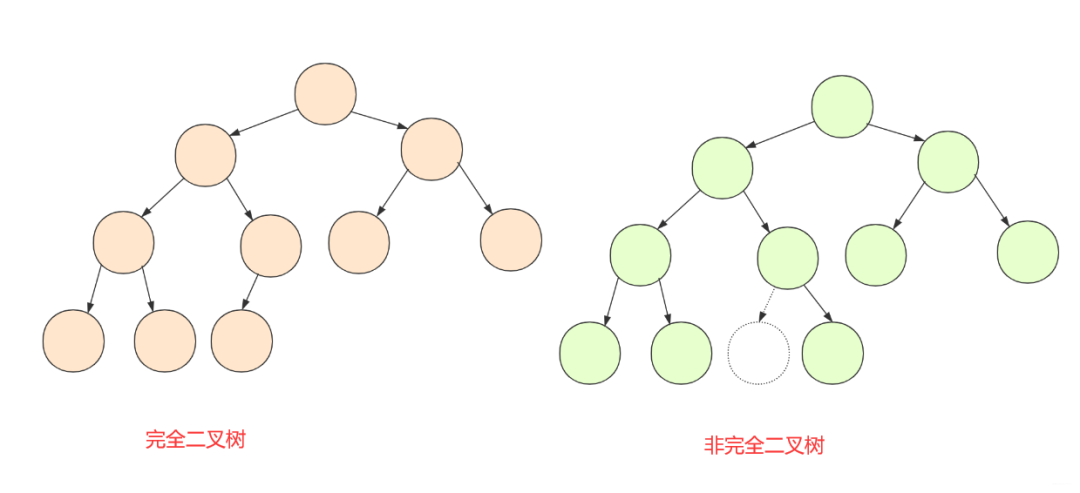
堆是一棵完全二叉树
每个节点总是大于(或小于)它的孩子节点。
完全二叉树
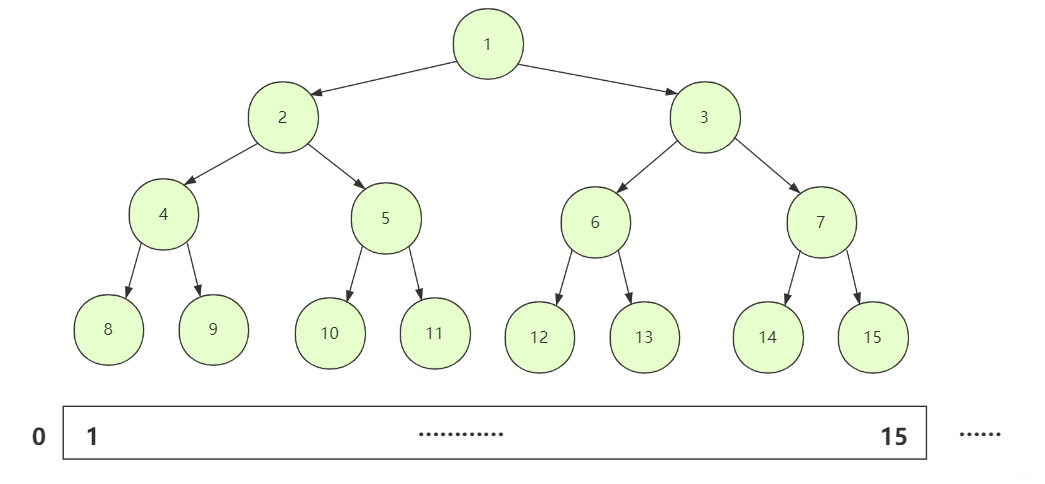
看作树的数组对象 我们都知道我们排序的对象一般都是对数组之类的序列进行排序,如果转成抽象数据结构再实现可能成本比较大。
我们正常在构造一棵二叉树的时候通常采用链式left,right节点,但其实二叉树的表示方式用数组也可以实现,只不过普通的二叉树如果用数组储存可能空间利用 效率会很低而很少采用,但我们的堆是一颗完全二叉树。使用数组储存空间使用效率也比较高,所以在形式上我们把这个数组看成对应的完全二叉树,而操作上可以直接操作数组也比较方便。
在这里插入图片描述
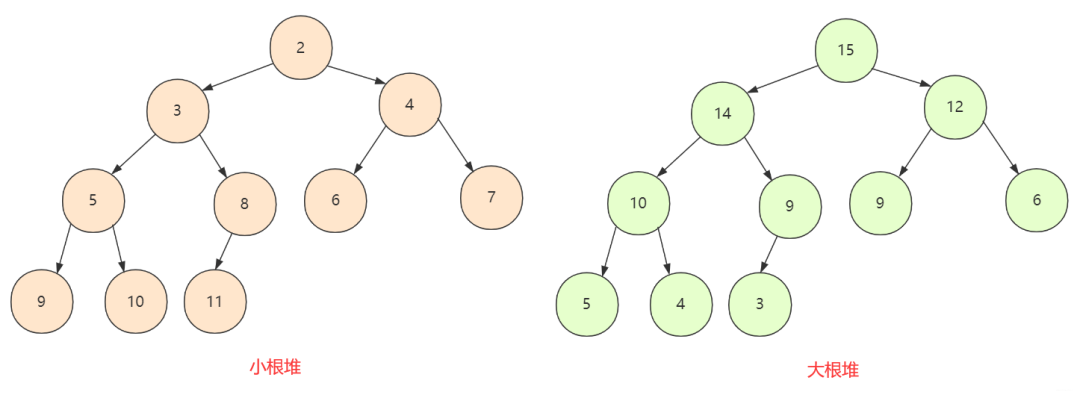
大根堆 VS 小根堆
堆排序 通过上面的介绍,我想你对堆应该有了一定的认识,堆排序肯定是借助堆实现的某种排序,其实堆排序的整体思路也很简单,就是
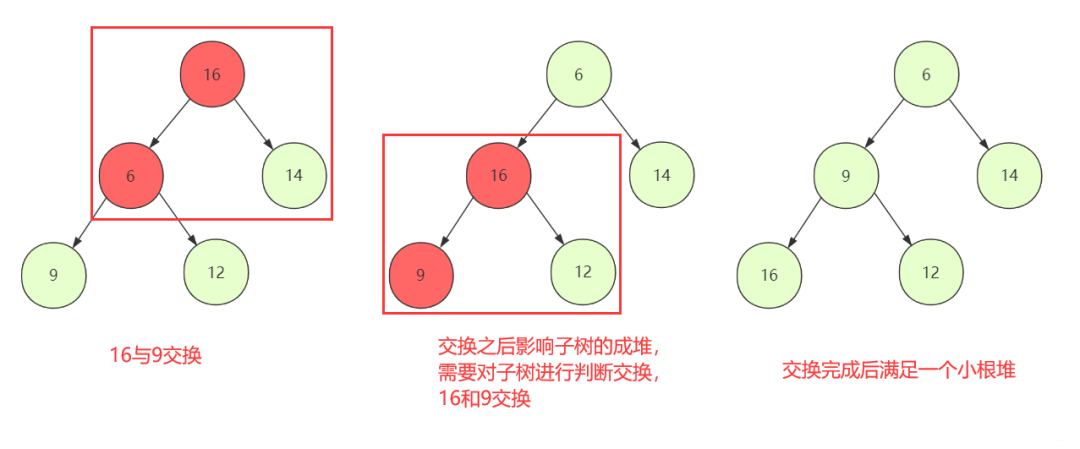
建堆 如果给一个无序的序列,首先要给它建成一个堆,我们如何实现这个操作呢?以下拿一个小根堆为例进行分析。
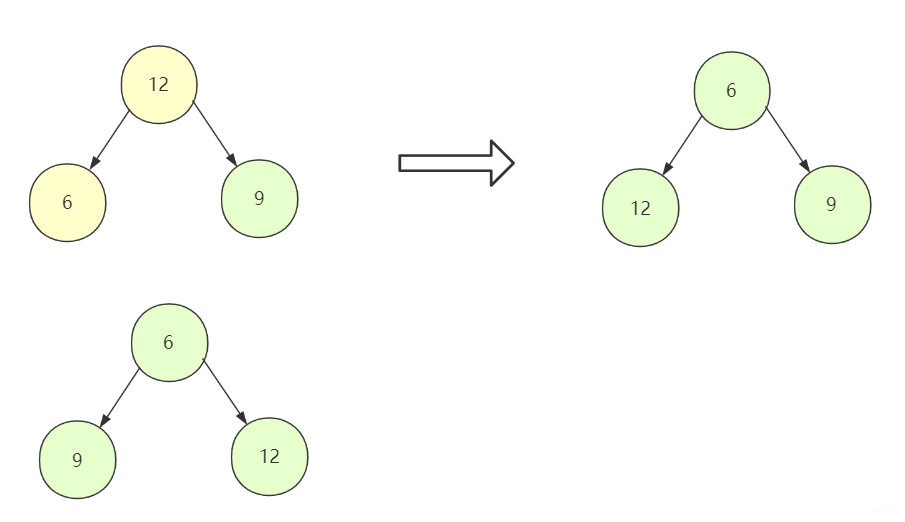
对于二叉树(数组表示),我们从下往上进行调整,从第一个非叶子节点 开始向前调整,对于调整的规则如下:
①对于小根堆,当前节点与左右孩子比较,如果均小于左右孩子节点,那么它本身就是一个小根堆,它不需要做任何改变,如果左右有孩子节点比它还小,那么就要和最小的那个进行替换。
②但是普通节点替换可能没问题,对于某些和子节点替换有可能改变子树成堆,所以需要继续往下判断交换(最差判断到叶子节点)。
分析构造堆的这个过程,每个非叶子节点都需要判断比较是否交换,这样一层就是O(n),而每个节点可能替换之后影响子节点成堆需要再往下判断遍历,你可能会认为它是一个O(nlogn),但其实你看看二叉树性值,大部分都是在底部的,上面的只有很少个数,如果你用数学方法去求得最终的复杂度它还是一个O(n)级别,这里就不作详细介绍了。
一个大根堆建立过程 也是一样的:
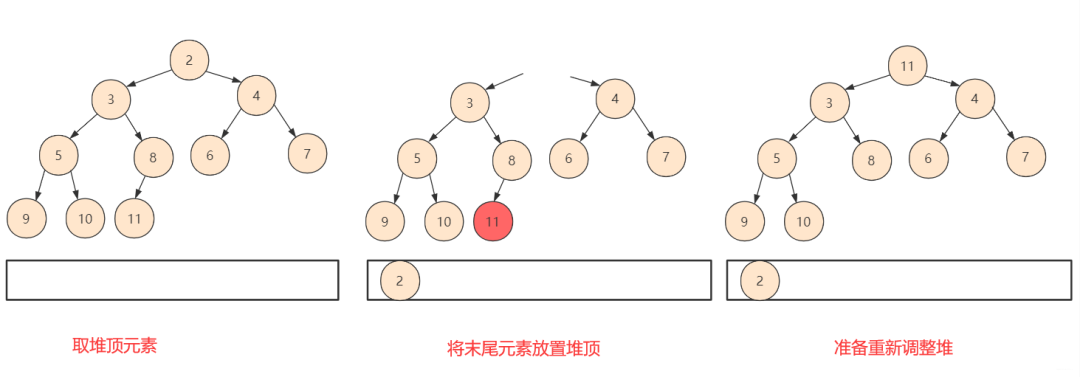
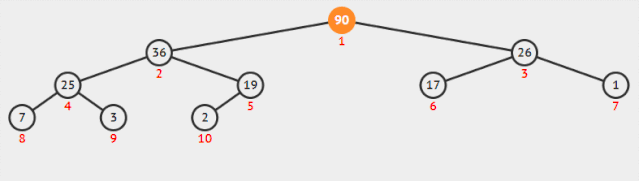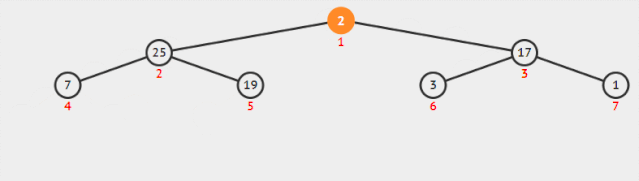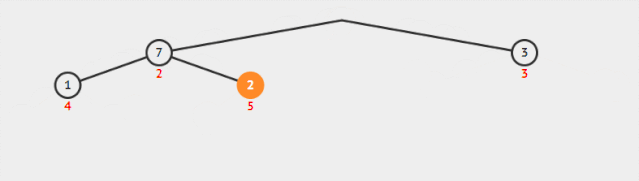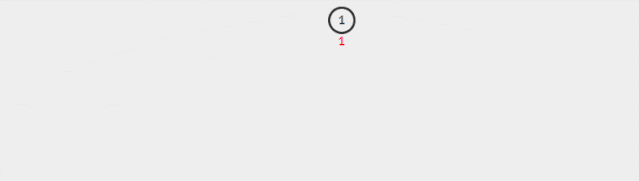
堆排序 上面的一个堆建造完毕之后,我们怎么去利用这个堆实现排序呢?答案也是很简单的,我们知道堆有一个特性就是堆顶是最小(或最大),而我们建造这个如果去除第一个元素,剩余左右孩子依然满足堆的性质 。
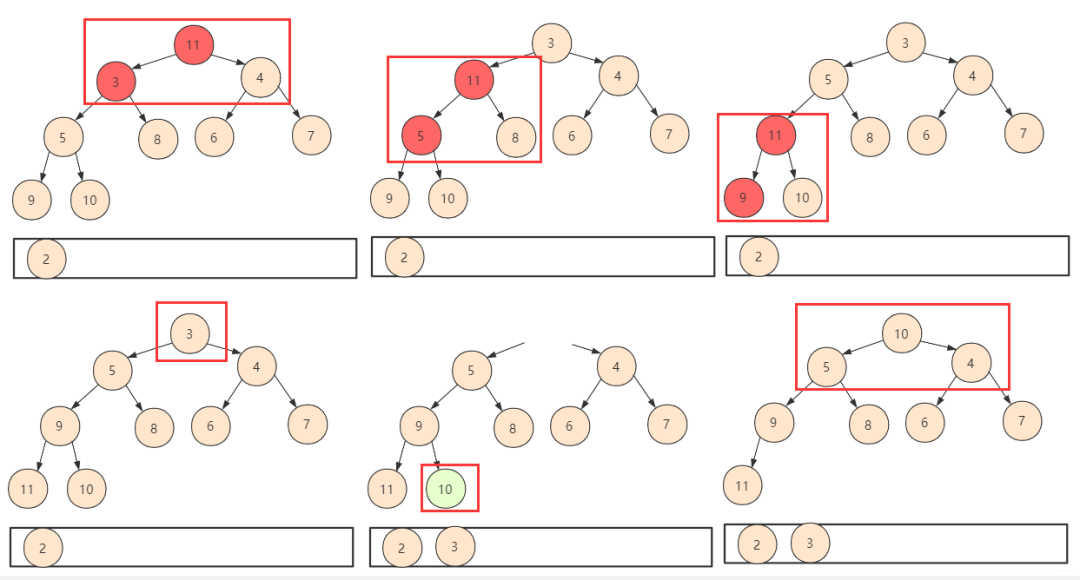
将 最后一个元素放置堆顶 ,由于第一个元素的存在使得整个不满足堆 的性质。 分析这个结构,和我们前面构造堆的过程中构造到第一个元素的操作相同:
这样到最后,堆排序即可完成,最终得到的序列即为堆排序序列。
一个大根堆的排序过程 如下:
具体实现 有了上述的思想之后,如何具体的实现这个堆排序的代码呢?
给定数组建堆(creatHeap)
堆构造完成,取第一个堆顶元素为最小(最大),剩下左右孩子依然满足堆的性值,但是缺个堆顶元素,如果给孩子调上来,可能会调动太多并且可能破坏堆结构。
而堆算法复杂度的分析上,之前建堆时间复杂度是O(n)。而每次删除堆顶然后需要向下交换,每个个数最坏为logn个。这样复杂度就为O(nlogn).总的时间复杂度为O(n)+O(nlogn)=O(nlogn).
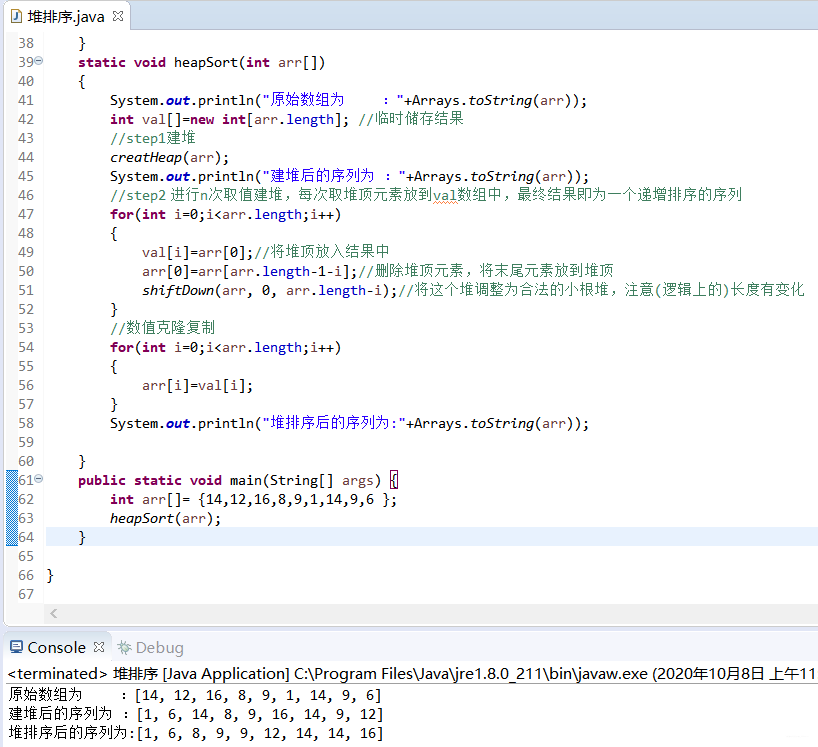
具体实现的代码如下:
import java.util.Arrays;public class 堆排序 static void swap (int arr[],int m,int n) int team=arr[m];//下移交换 把当前节点有效变换成一个堆(小根) static void shiftDown (int arr[],int index,int len) //0 号位置不用 int leftchild=index*2 +1 ;//左孩子 int rightchild=index*2 +2 ;//右孩子 if (leftchild>=len)return ;else if (rightchild<len&&arr[rightchild]<arr[index]&&arr[rightchild]<arr[leftchild])//右孩子在范围内并且应该交换 //交换节点值 //可能会对孩子节点的堆有影响,向下重构 else if (arr[leftchild]<arr[index])//交换左孩子 //将数组创建成堆 static void creatHeap (int arr[]) for (int i=arr.length/2 ;i>=0 ;i--)static void heapSort (int arr[]) "原始数组为 :" +Arrays.toString(arr));int val[]=new int [arr.length]; //临时储存结果 //step1建堆 "建堆后的序列为 :" +Arrays.toString(arr));//step2 进行n次取值建堆,每次取堆顶元素放到val数组中,最终结果即为一个递增排序的序列 for (int i=0 ;i<arr.length;i++)0 ];//将堆顶放入结果中 0 ]=arr[arr.length-1 -i];//删除堆顶元素,将末尾元素放到堆顶 0 , arr.length-i);//将这个堆调整为合法的小根堆,注意(逻辑上的)长度有变化 //数值克隆复制 for (int i=0 ;i<arr.length;i++)"堆排序后的序列为:" +Arrays.toString(arr));public static void main (String[] args) int arr[]= {14 ,12 ,16 ,8 ,9 ,1 ,14 ,9 ,6 };执行结果:
在这里插入图片描述
当然,代码为了成章节我把它命名为中文,还有些不规范的地方请注意甄别。
结语 对于堆排序就先介绍到这里了,当然堆的强大之处不止这么一点,优先队列同样也是用到堆但是这里就不详细介绍了,我相信优秀的你肯定又掌握了一门O(nlogn)级别的排序算法啦。如果写的有啥不确切地方还请指正。
最后,如果感觉不错一键三联 哦!,欢迎关注公众号:bigsai,更多精彩等你来看。期待你的关注,并且笔者也准备了一波pdf学习资源分享给你。
另外欢迎添加笔者微信交流:
点赞、在看二连