选择排序法
第1趟,在待排序记录r[1]~r[n]中选出最小的记录,将它与r[1]交换;第2趟,在待排序记录r[2]~r[n]中选出最小的记录,将它与r[2]交换;以此类推,第i趟在待排序记录r[i]~r[n]中选出最小的记录,将它与r[i]交换,使有序序列不断增长直到全部排序完毕。
初始序列:{ 49 27 65 97 76 12 38 }
第1趟:12与49交换:12 { 27 65 97 76 49 38 }
第2趟:27不动:12 27 { 65 97 76 49 38 }
第3趟:65与38交换:12 27 38 { 97 76 49 65 }
第4趟:97与49交换:12 27 38 49 { 76 97 65 }
第5趟:65与76交换:12 27 38 49 65 { 97 76 }
第6趟:97与76交换:12 27 38 49 65 76 97 完成
代码
public class Sort {
public static void main(String[] args) {
int[] i = { 1, 5, 6, 12, 4, 9, 3, 23, 39, 403, 596, 87 };
System.out.println("结果:");
xuanZe(i);
System.out.println();
}
// 选择排序算法
public static void xuanZe(int[] x) {
for (int i = 0; i < x.length; i++) {
int lowerIndex = i;
// 找出最小的一个索引
for (int j = i + 1; j < x.length; j++) {
if (x[j] < x[lowerIndex]) {
lowerIndex = j;
}
}
// 交换
int temp = x[i];
x[i] = x[lowerIndex];
x[lowerIndex] = temp;
}
for (int i : x) {
System.out.print(i + " ");
}
}
}
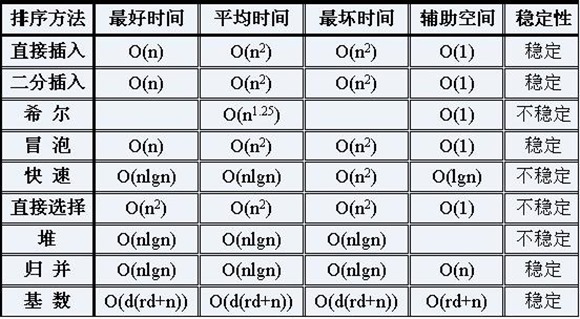
时间复杂度为O(N2) 。
希尔排序
对于n个元素的数组,假设增量为 h:
第一趟 : 从第1个元素开始,每隔h取一个元素,那么最后可以得到n/h个元素,一边取,一边通过直接插入将这h个元素排序
第二趟 : 从第2个元素开始,每隔h取一个元素,跟第一趟一样。
...
第h趟 : 从第h个元素开始,每隔h取一个元素,跟第一趟一样。
(此时,整个数组还不是有序的)
然后,减少h的值,重复上面的操作,直到h减小为1,排序完成。
![1 1]()
代码
public static void sort(int[] nums) {
int len = nums.length / 2;
while (len >=1) {
for (int i = 0; i < len; i++) {
// 直接插入排序对分组进行排序
for (int k = i; k < nums.length-len; k +=len) {
int j = k + len;
int temp = nums[j];
while (k >= 0 && nums[k] > temp) {
nums[j] = nums[k];
k -= len;
j -= len;
}
nums[j] = temp;
}
}
len = len/2;
}
}
时间复杂度是O(N*lgN)。
二分插入排序
二分查找插入排序的原理:是直接插入排序的一个变种,区别是:在有序区中查找新元素插入位置时,为了减少元素比较次数提高效率,采用二分查找算法进行插入位置的确定。
代码
public class BinarySearch1 {
public static void main(String args[])
{
int array[]={49,38,65,97,76,13,27};
binarySort(array,array.length);
System.out.println(Arrays.toString(array));
}
//二分查找
public static int binarySearch(int array[],int low,int high,int temp)
{
int mid=0;
while(low<=high)
{
mid=(low+high)/2;
if(array[mid]<temp&&temp<=array[mid+1])
return (mid+1);
else if(array[mid]<temp)
low = mid + 1;
else
high = mid -1;
}
return high;
}
//二分排序
public static void binarySort(int array[],int size)
{
int i,j,k,temp;
for(i=1;i<size;i++)
{
temp=array[i];
if(array[i]<array[0])
k=0;
else
k = binarySearch(array,0,i,temp);
for(j=i;j>k;j--)
{
array[j]=array[j-1];
}
array[k]=temp;
System.out.println(Arrays.toString(array));
}
}
}
时间复杂度为O(N2) ;空间复杂度为O(1)。
我是天王盖地虎的分割线
![1 1]()
本文转自我爱物联网博客园博客,原文链接:http://www.cnblogs.com/yydcdut/p/3860460.html,如需转载请自行联系原作者