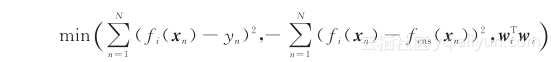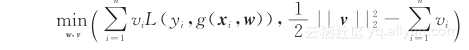8.11 监督学习

监督学习从有标记的示例数据学习模型，示例数据包含了样本对应的标记，标记指定了该样本上模型应有的输出，监督学习方法通过在一定的模型空间进行搜索，找到符合示例数据的模型。其中模型的寻找过程就是一类优化问题，而且寻找最优模型通常都是 NP 难的问题。演化算法的优化能力能够帮助监督学习寻找到更好的模型。

人工神经网络[8]是一类常用的学习模型，近年来深度学习的发展使得神经网络已成为人工智能领域的研究热点，其在诸多领域（如图像识别、语音识别等）取得成功应用。针对神经网络的训练很多情况下可以视为一个单目标优化问题，在人工设定好网络结构的前提下，优化网络权值，其目标函数涉及实际输出和期望输出之间的误差、网络的复杂度等因素。神经网络往往包含多层神经元，并且使用非线性激活函数，因而神经网络的优化面临包含大量局部极值的优化问题，基于梯度下降的优化方法往往只能收敛到局部最优或是某不动点，如果将神经网络结构也作为优化的参数，则优化问题更为困难。

演化算法由于具备更强的搜索能力且对优化问题性质要求极少，在上世纪 90 年代神经网络的上一波热潮时期已被用于神经网络模型的学习[9] ，回顾以往的研究，演化算法在神经网络学习的应用主要可以分成连接权重的优化、网络结构的优化以及学习规则（learning rule）的优化三个层面。对于连接权重，编码方式可采用二进制或者实值；在评估目标函数值时，网络结构一般预先给定。文献 [10]在图像分类数据上的实验结果显示：相比使用反向传播算法优化前向神经网络的连接权重，使用演化算法能够快速地找到更好的连接权重。文献 [11-12]通过工程设计、图像识别、手写数字识别上的实验得出：将演化算法和基于梯度的优化方法相结合（即演化算法找到的连接权重作为梯度优化方法的初始权重）能够进一步改进连接权重的质量。演化算法执行全局搜索，能够避免梯度优化方法易于陷入局部最优的缺点而找到接近全局最优的连接权重；在此基础上执行基于梯度的优化方法，能够利用其局部搜索能力，进一步快速地改进连接权重的质量。对于网络结构，则可以采用一个 0、1 矩阵来表示，取值为 1 表示相应两个节点之间有连接；取值为 0则相反。在评估适应度值时，学习规则一般预先给定，然后在不同的初始权重和学习规则参数下分别训练，以平均结果来衡量适应度值。为了减少网络结构适应度评估的噪声，网络结构和连接权重往往被同时优化。文献 [13] 在医疗诊断、信用卡评估等问题上的实验结果显示：使用演化算法同时优化网络结构和连接权重能够得到复杂度更低、泛化能力更好的神经网络。演化算法还可用于优化学习规则参数，甚至学习得到有效的新规则。有趣的是，随着神经网络再次成为热潮，近来也开始出现演化神经网络的工作[14-16] 。

神经网络也已被用于多标记学习。不同于传统监督学习，在多标记学习框架下，每一个训练样本被赋予一组类别标记组成的标记集合而非单个标记，而学习的任务也变成为未见到的样本预测所有相关的类别标记[17] 。目前，不少多标记学习的评价指标已经被提出，比如 Ranking Loss、HammingLoss、Micro F1 等。以往的多标记学习方法都是去优化单个指标，但是在很多实际应用中，一个最优的多标记学习器需要同时考虑多个可能冲突的指标，比如最小化 Hamming Loss 的同时最大化Micro F1。文献 [18] 以 RBF 神经网络作为多标记学习器，提出了一种多目标演化算法 MOML 用于同时优化多标记学习任务的多个指标，实验结果显示出 MOML 不仅能够得到一组可以满足不同用户需求的多标记学习器，同时还能提高在大多数指标上的性能。

集成学习通过集成多个学习器获得比单个学习器更好的学习效果[19] 。一般认为，基学习器的精度越好，差异越大，集成后的性能就越好。文献 [20]采用 RBF 神经网络作为基学习器，将集成学习形式化成一个三目标优化问题：
其中，第 1 项代表第 i 个学习器的误差；第 2 项代表第 i 个学习器和其他学习器之间的差异；第 3 项则表示对第 i 个学习器的正则化。基于 NSGA 框架[21]的一种多目标演化算法被提出用于求解该三目标优化问题，最终种群中包含的所有基学习器被集成作为输出。大量的实验结果表明了该方法的优越性。

演化算法还被用于集成剪枝[19] 。在集成学习的基础上，集成剪枝从所有训练好的学习器中选择一部分集成，力图使所选学习器子集进一步提升泛化性能，且包含学习器数目尽可能少，从而减少存储计算开销。一方面，如果赋予每个学习器一个权重系数，所有学习器的集成被表示成一个权重向量。演化算法通过最小化在验证集上的错误率，试图找到最优权重向量；然后将权重小于某个阈值的学习器删除，获得最终的学习器子集。另一方面，如果将学习器子集表示成一个 0/1 向量，表示模型的选择，演化算法可直接搜索最优子集，避免了采用实值权重向量带来的阈值设定问题。已有实验结果显示演化算法可以大大减少学习器数目，并提升泛化性能。

自步学习（self-paced learning）通过模拟人的认知机理，将学习对象 ( 数据、特征、概念等 )按其对学习目标的难易程度，从易到难开展学习，以这种方式让机器完成复杂的学习与推理任务[22] 。文献 [23] 将自步学习形式化成一个二目标优化问题：
其中，第 1 项是错误率；第 2 项是自步学习的正则化项。基于 MOEA/D [6] 提出了一种多目标演化算法MOSPL，并通过依次增加训练样本数来迭代求解该问题。在矩阵分解和动作识别上的实验结果显示了 MOSPL 的优越性能。