详解Spring Boot的RedisAutoConfiguration配置-低调大师

详解Spring Boot的RedisAutoConfiguration配置

2024-06-14 302

本文分享自华为云社区《【Spring Boot 源码学习】RedisAutoConfiguration 详解》，作者： Huazie。

引言

带大家分析 Spring Boot 内置的有关 Redis 的自动配置类【RedisAutoConfiguration】。

1. Spring Data Redis

Spring Data Redis 是 Spring Data 家族的一部分，它提供了从 Spring 应用程序中轻松配置和访问 Redis 的功能。

我们来看看官方介绍的特性：

连接包作为多个 Redis 驱动程序（ Lettuce 和 Jedis ）的低级别抽象。
将 Redis 驱动程序异常转换为 Spring 的可移植数据访问异常层次结构。
提供各种 Redis 操作、异常转换和序列化支持的 RedisTemplate。
支持发布订阅（例如用于消息驱动 POJO 的消息监听器容器）。
支持 Redis Sentinel 和 Redis Cluster。
使用 Lettuce 驱动程序的响应式 API。
支持 JDK、String、JSON和 Spring 对象 / XML 映射序列化器。
在 Redis 上实现 JDK 集合。
支持原子计数器类。
支持排序和管道功能。
专用于 SORT、SORT/GET模式和支持返回批量值的功能。
为 Spring 缓存抽象提供 Redis 实现。
自动实现 Repository 接口，包括使用 @EnableRedisRepositories 支持自定义查询方法。
对存储库提供 CDI 支持。

在 Spring Data Redis 中，我们可以直接使用 RedisTemplate 及其相关的类来操作 Redis。虽然 RedisConnection 提供了接受和返回二进制值（字节数组）的低级方法，但 RedisTemplate 负责序列化和连接管理，使用户可以无需处理这些细节。

RedisTemplate 还提供了操作视图（按照 Redis 命令参考进行分组），这些视图提供了丰富、通用的接口，用于针对特定类型或特定键进行操作（通过 KeyBound 接口实现），如下表所示：

下面我们来看看相关的 Spring 配置：

<?xml version="1.0" encoding="UTF-8"?>
<beans xmlns="http://www.springframework.org/schema/beans"
  xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
  xmlns:p="http://www.springframework.org/schema/p"
  xsi:schemaLocation="http://www.springframework.org/schema/beans https://www.springframework.org/schema/beans/spring-beans.xsd">

  <bean id="jedisConnFactory" class="org.springframework.data.redis.connection.jedis.JedisConnectionFactory" p:use-pool="true"/>
  <!-- redis 模板定义 -->
  <bean id="redisTemplate" class="org.springframework.data.redis.core.RedisTemplate" p:connection-factory-ref="jedisConnFactory"/>

</beans>

一旦配置完成，Redis 模板就是线程安全的，并且可以在多个实例之间重用。

RedisTemplate 使用基于 Java 的序列化器进行大部分操作。也就意味着通过模板写入或读取的任何对象都是通过 Java 进行序列化和反序列化的。

我们也可以更改模板上的序列化机制，可以添加如下配置：

<bean id="redisTemplate" class="org.springframework.data.redis.core.RedisTemplate">
    <property name="connectionFactory" ref="redisConnectionFactory"/>
    <property name="keySerializer">
        <bean class="org.springframework.data.redis.serializer.StringRedisSerializer"/>
    </property>
    <property name="valueSerializer">
        <bean class="org.springframework.data.redis.serializer.JdkSerializationRedisSerializer"/>
    </property>
    <property name="hashKeySerializer">
        <bean class="org.springframework.data.redis.serializer.StringRedisSerializer"/>
    </property>
    <property name="hashValueSerializer">
        <bean class="org.springframework.data.redis.serializer.JdkSerializationRedisSerializer"/>
    </property>
</bean>

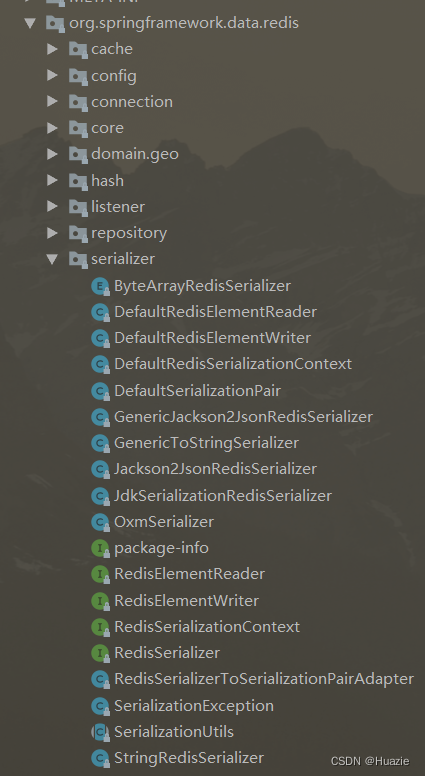
而 Redis 模块提供了几个序列化器的实现，有关这些实现大家可以查看 org.springframework.data.redis.serializer 包。

还可以将任何序列化程序设置为 null，并通过设置 enableDefaultSerializer 属性为 false 来使用RedisTemplate 与原始字节数组一起使用。

注意：模板要求所有键都不为空。但是，只要底层序列化程序接受值，值就可以为空。

下面我们可以注入 RedisTemplate，并调用 RedisTemplate 的方法进行存储、查询、删除等操作。

@Autowired
private RedisTemplate<String, Object> redisTemplate;
// 存储数据
redisTemplate.opsForValue().set("key", "value");
// 查询数据
Object value = redisTemplate.opsForValue().get("key");
// 删除数据
redisTemplate.delete("key");

对于需要特定模板视图的情况，声明视图作为依赖项并注入模板。容器会自动执行转换，消除opsFor[X] 调用，如下所示的示例：

public class Example {	
	// inject the template as ListOperations
	@Resource(name="redisTemplate")
	private ListOperations<String, String> listOps;
	
	public void addLink(String userId, URL url) {
	  listOps.leftPush(userId, url.toExternalForm());
	}
}

当然 Spring Data Redis 肯定不止上述这些，有需要深入了解的读者们，请看如下：

参考： Spring Data Redis 官方文档

2. RedisAutoConfiguration

那么 Spring Data Redis 的 RedisTemplate 的自动配置在 Spring Boot 是如何实现的呢？

Spring Boot 是通过内置的 RedisAutoConfiguration 配置类来完成这一功能。下面我们具体分析一下：

注意： 以下涉及 Spring Boot 源码均来自版本 2.7.9，其他版本有所出入，可自行查看源码。

2.1 加载自动配置组件

从之前的《【Spring Boot 源码学习】自动装配流程源码解析（上）》中，我们知道 Spring Boot 内部针对自动配置类，会读取如下两个配置文件：

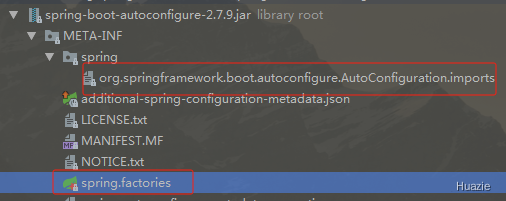
META-INF/spring.factories
META-INF/spring/org.springframework.boot.autoconfigure.AutoConfiguration.imports

实际上在 Spring Boot 2.7.9 版本中， Spring Boot 自己内部的 META-INF/spring.factories 中有关自动配置的注册类的配置信息已经被去除掉了，不过其他外围的 jar 中可能有自己的 META-INF/spring.factories 文件，它里面也有关于自动配置注册类的配置信息；

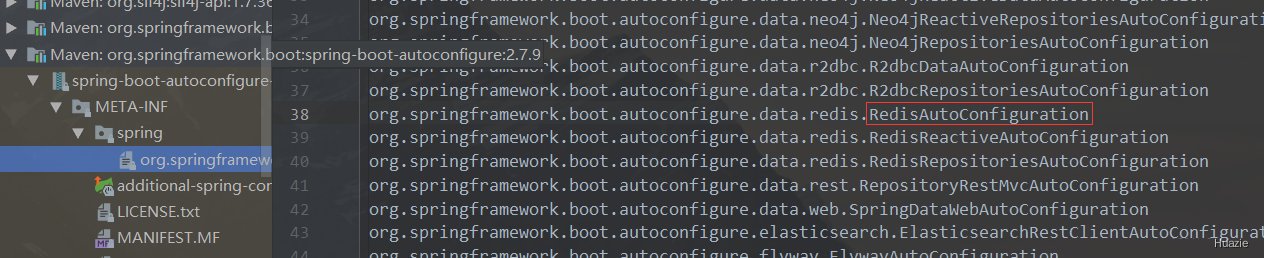
而 Spring Boot 内置的 RedisAutoConfiguration 配置类，则是配置在上述的第二个配置文件 META-INF/spring/org.springframework.boot.autoconfigure.AutoConfiguration.imports 中。

2.2 过滤自动配置组件

上述自动配置加载完之后，就来到了《【Spring Boot 源码学习】自动装配流程源码解析（下）》介绍的 过滤自动配置组件 逻辑。

这部分数据对应的配置内容在 META-INF/spring-autoconfigure-metadata.properties 文件中：

org.springframework.boot.autoconfigure.data.redis.RedisAutoConfiguration=
org.springframework.boot.autoconfigure.data.redis.RedisAutoConfiguration.ConditionalOnClass=org.springframework.data.redis.core.RedisOperations

显然这里涉及到了 ConditionalOnClass 注解，我们翻看 RedisAutoConfiguration 配置类的源码，如下：

@AutoConfiguration
@ConditionalOnClass(RedisOperations.class)
@EnableConfigurationProperties(RedisProperties.class)
@Import({ LettuceConnectionConfiguration.class, JedisConnectionConfiguration.class })
public class RedisAutoConfiguration {

	@Bean
	@ConditionalOnMissingBean(name = "redisTemplate")
	@ConditionalOnSingleCandidate(RedisConnectionFactory.class)
	public RedisTemplate<Object, Object> redisTemplate(RedisConnectionFactory redisConnectionFactory) {
		// 。。。
	}

	@Bean
	@ConditionalOnMissingBean
	@ConditionalOnSingleCandidate(RedisConnectionFactory.class)
	public StringRedisTemplate stringRedisTemplate(RedisConnectionFactory redisConnectionFactory) {
		// 。。。
	}

}

2.2.1 涉及注解

我们先来看看上述 RedisAutoConfiguration 配置类涉及到的注解，如下：

@AutoConfiguration : 该类是一个自动配置类，Spring Boot 会根据项目中的依赖自动配置这个类的实例。
@ConditionalOnClass(RedisOperations.class) ：只有在项目中引入了 RedisOperations 类（通常由 spring-data-redis 库提供）的情况下，才会加载这个配置类。
@EnableConfigurationProperties(RedisProperties.class) ：启用RedisProperties 类作为配置属性。这样，我们就可以在 application.properties 或application.yml 文件中定义 Redis 的相关配置。
@Import({ LettuceConnectionConfiguration.class, JedisConnectionConfiguration.class }) ：导入注解，表示导入 LettuceConnectionConfiguration 和 JedisConnectionConfiguration 这两个类。这两个类通常用于配置 Redis 连接的具体实现，例如使用 Lettuce 还是 Jedis 等。
@Bean ：用于声明一个方法创建的对象是一个 Spring 管理的 Bean。Spring 容器会自动管理这个 Bean 的生命周期，包括依赖注入、初始化和销毁等。
@ConditionalOnMissingBean ：只有在当前 Spring 容器中不存在指定类型的 Bean 时，才会执行被注解的方法。这样可以用于确保在需要的时候才创建某个 Bean，避免重复创建。
@ConditionalOnSingleCandidate：只有在当前上下文中存在且只有一个指定类型的 bean 候选者时，才会创建这个 bean。

2.2.2 RedisProperties

其中 RedisProperties 类的属性值对应着 application.yml 或 application.properties 中的配置，通过注解@ConfigurationProperties(prefix = "spring.redis") 实现的属性注入。

有关属性注入的内容后续笔者会另外介绍，我们先来看看RedisProperties 类相关的部分源码和对应的配置参数：

@ConfigurationProperties(prefix = "spring.redis")
public class RedisProperties {

	// 。。。

	// Redis 服务器主机地址.
	private String host = "localhost";
	
	// 。。。

	// Redis 服务器的端口
	private int port = 6379;

	private Sentinel sentinel;

	private Cluster cluster;

	private final Jedis jedis = new Jedis();

	private final Lettuce lettuce = new Lettuce();

	// Redis 连接池配置
	public static class Pool {
		// 。。。
	}
	// Redis 集群配置
	public static class Cluster {
		// 。。。
	}
	// Redis 哨兵配置
	public static class Sentinel {
		// 。。。
	}
	// Jedis 客户端配置
	public static class Jedis {

		// Jedis 连接池配置
		private final Pool pool = new Pool();
	}
	// Lettuce 客户端配置
	public static class Lettuce {
		// Lettuce 连接池配置
		private final Pool pool = new Pool();

		private final Cluster cluster = new Cluster();
	}
}

然后在 application.properties 中，我们就可以添加类似如下的配置：

# Redis 单机配置
spring.redis.host=127.0.0.1
spring.redis.port=31113

# Redis 集群配置
# nodes属性是Redis集群节点的地址和端口，用逗号分隔。
spring.redis.cluster.nodes=192.168.1.1:7000,192.168.1.2:7001,192.168.1.3:7002
# max-redirects属性是最大重定向次数，用于处理节点故障的情况。
spring.redis.cluster.max-redirects=3

# mymaster是哨兵模式下的主节点名称。
spring.redis.sentinel.master=mymaster
# nodes是哨兵模式下的从节点地址和端口。
spring.redis.sentinel.nodes=192.168.1.1:26379,192.168.1.2:26379,192.168.1.3:26379

# ...其他配置省略

2.3 redisTemplate 方法

先来看看 redisTemplate 方法的源码【Spring Boot 2.7.9】：

@Bean
@ConditionalOnMissingBean(name = "redisTemplate")
@ConditionalOnSingleCandidate(RedisConnectionFactory.class)
public RedisTemplate<Object, Object> redisTemplate(RedisConnectionFactory redisConnectionFactory) {
	RedisTemplate<Object, Object> template = new RedisTemplate<>();
	template.setConnectionFactory(redisConnectionFactory);
	return template;
}

上述逻辑表示只有在当前上下文中不存在名为 "redisTemplate" 的 Bean 时，才会创建一个名为 redisTemplate 的 RedisTemplate Bean，并将其与一个可用的 Redis 连接工厂关联起来。

2.4 stringRedisTemplate 方法

我们再来看看 stringRedisTemplate 方法的源码【Spring Boot 2.7.9】：

@Bean
@ConditionalOnMissingBean
@ConditionalOnSingleCandidate(RedisConnectionFactory.class)
public StringRedisTemplate stringRedisTemplate(RedisConnectionFactory redisConnectionFactory) {
	return new StringRedisTemplate(redisConnectionFactory);
}

上述逻辑也好理解，它表示只有在当前上下文中不存在名为 "stringRedisTemplate" 的 Bean 时，才会创建一个名为stringRedisTemplate的 StringRedisTemplate Bean，并将其与一个可用的 Redis 连接工厂关联起来。

StringRedisTemplate 是 RedisTemplate 的子类，专门用于处理字符串类型的数据。

StringRedisTemplate 使用的是 StringRedisSerializer，它在存入数据时会将数据先序列化成字节数组。

默认情况下，StringRedisTemplate 采用的序列化策略有两种：

String 的序列化策略，
JDK 的序列化策略。

总结

本篇我们深入分析了 RedisAutoConfiguration 配置类的相关内容，进一步加深了对自动配置装配流程的了解。

点击关注，第一时间了解华为云新鲜技术~

微信关注我们

原文链接：https://my.oschina.net/u/4526289/blog/11209334

转载内容版权归作者及来源网站所有！

低调大师中文资讯倾力打造互联网数据资讯、行业资源、电子商务、移动互联网、网络营销平台。持续更新报道IT业界、互联网、市场资讯、驱动更新,是最及时权威的产业资讯及硬件资讯报道平台。

技术解密Java Chassis 3超实用的可观测性

本文分享自华为云社区《Java Chassis 3技术解密：实用的可观测性》，作者：liubao68。狭义的可观测性，指日志、调用链和指标，广义的可观测性则包含更多的内容，一般的，应用程序暴露出来的便于理解其运行状态、运行轨迹、内部结构和功能集合的信息，都是可观测性的范围，本文只讨论狭义的可观测性。日志揭露了应用程序内部运行的轨迹，通过异常日志，可以理解错误产生的原因；调用链反映的是一次业务操作经过的关键处理节点，可以帮助快速确定问题发生的边界；指标反映错误发生时应用程序的当前或者历史状态，帮助分析需要一定的时间或者流量积累才会发生的问题，比如过载问题、性能问题等。可以看出，为了分析故障，具备可观测性能力非常重要。微服务系统具备复杂的调用关系和分布式部署特征，为了更好的分析和处理日志、调用链和指标，通常会部署ELK、SkyWalking和Prometheus等外部系统。这些系统完全搭建起来，会花费数十万每年的计算成本，而且很可能并没有显著提升日常问题定位的效率，不恰当的使用还可能会引入性能问题。针对问题定位难的情况，Java Chassis 3提供了非常简单高效，而且低成本的解决...

2024-06-14

249

PrimiHub一款由密码学专家团队打造的开源隐私计算平台，专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。在现代密码学中，椭圆曲线加密算法（Elliptic Curve Cryptography, ECC）因其高效的加密速度、较小的密钥尺寸和较高的安全性而受到广泛关注。ECC基于椭圆曲线数学，利用椭圆曲线上的点构成的阿贝尔群和相应的离散对数问题来实现加密和数字签名。ECC的安全性依赖于椭圆曲线离散对数问题（Elliptic Curve Discrete Logarithm Problem, ECDLP）的难解性。本文将深入分析ECC中公钥与私钥的互换性问题，探讨这种互换在理论和实际应用中的可能性及其影响。椭圆曲线加密算法基础椭圆曲线的定义椭圆曲线是一种定义在有限域上的代数曲线，其标准方程为： [ y^2 = x^3 + ax + b ] 其中，(a) 和 (b) 是有限域中的元素，且满足 (4a^3 + 27b^2 \neq 0) 以确保曲线没有奇异点。这样的定义使得椭圆曲线可以构成一个具有丰富结构的代数系统，广泛应用于密码学。 ECC的密钥生成机制...

2024-06-17

306

资源下载

更多资源

Mario

马里奥是站在游戏界顶峰的超人气多面角色。马里奥靠吃蘑菇成长，特征是大鼻子、头戴帽子、身穿背带裤，还留着胡子。与他的双胞胎兄弟路易基一起，长年担任任天堂的招牌角色。

腾讯云软件源

为解决软件依赖安装时官方源访问速度慢的问题，腾讯云为一些软件搭建了缓存服务。您可以通过使用腾讯云软件源站来提升依赖包的安装速度。为了方便用户自由搭建服务架构，目前腾讯云软件源站支持公网访问和内网访问。

Nacos

Nacos /nɑ:kəʊs/ 是 Dynamic Naming and Configuration Service 的首字母简称，一个易于构建 AI Agent 应用的动态服务发现、配置管理和AI智能体管理平台。Nacos 致力于帮助您发现、配置和管理微服务及AI智能体应用。Nacos 提供了一组简单易用的特性集，帮助您快速实现动态服务发现、服务配置、服务元数据、流量管理。Nacos 帮助您更敏捷和容易地构建、交付和管理微服务平台。

Sublime Text

Sublime Text具有漂亮的用户界面和强大的功能，例如代码缩略图，Python的插件，代码段等。还可自定义键绑定，菜单和工具栏。Sublime Text 的主要功能包括：拼写检查，书签，完整的 Python API ， Goto 功能，即时项目切换，多选择，多窗口等等。Sublime Text 是一个跨平台的编辑器，同时支持Windows、Linux、Mac OS X等操作系统。