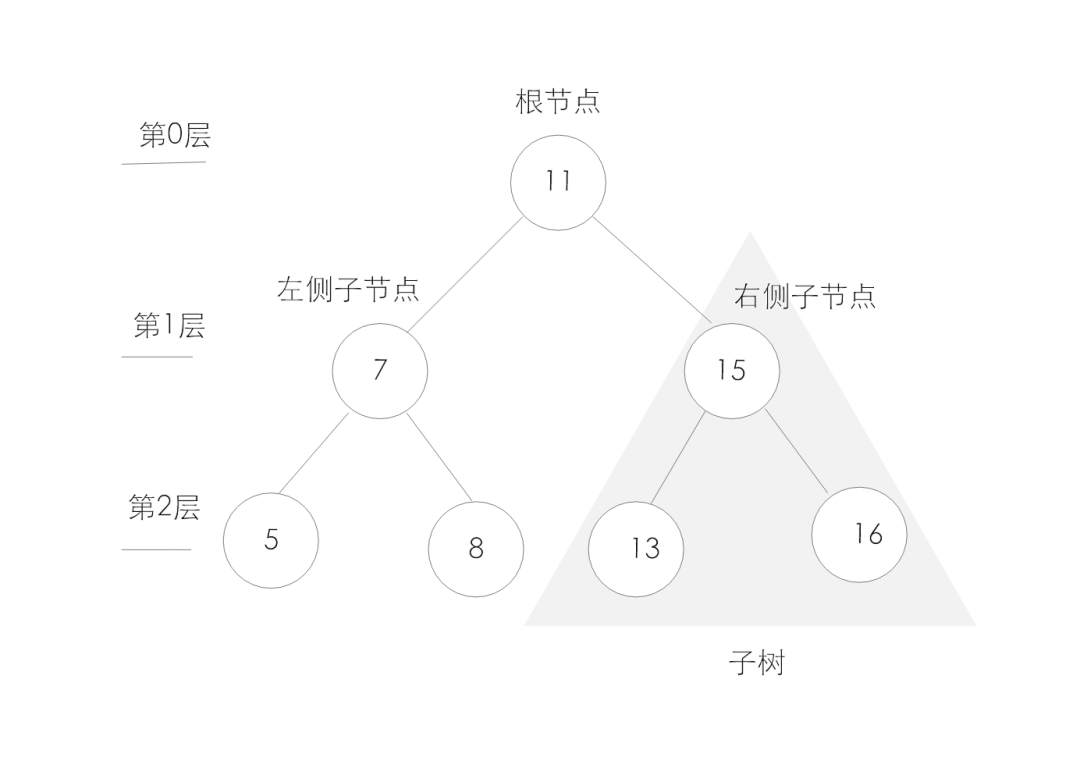
接下来让我们一起来探讨js数据结构中的树。这里的树类比现实生活中的树，有树干，树枝，在程序中树是一种数据结构，对于存储需要快速查找的数据非有用，它是一种分层数据的抽象模型。一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点以及零个或多个子节点。如下所以为一个树结构：）

和树相关的概念：1. 子树：由节点和他的后代构成，如上图标示处。2. 深度：节点的深度取决于它祖节点的数量，比如节点5有2个祖节点，他的深度为2。3. 高度：树的高度取决于所有节点深度的最大值。

二叉树和二叉搜索树介绍

1. 创建BinarySearchTree类

function BinarySearchTree(){
    // 用于创建节点的类
    let Node = function(key) {
        this.key = key;
        this.left = null;
        this.right = null;
    }
    // 根节点
    let root = null;
}

我们将使用和链表类似的指针方式去表示节点之间的关系，如果不了解链表，请看我后序的文章《如何实现单向链表和双向链表》。

2.插入一个键

// 插入一个键
this.insert = function(key) {
    let newNode = new Node(key);
    root === null ? (root = newNode) : (insertNode(root, newNode))
}

向树中插入一个新的节点主要有以下三部分：1.创建新节点的Node类实例 --> 2.判断插入操作是否为根节点,是根节点就将其指向根节点 --> 3.将节点加入非根节点的其他位置。

insertNode的具体实现如下：

function insertNode(node, newNode){
    if(newNode.key < node.key) {
        node.left === null ? (node.left = newNode) : (insertNode(node.left, newNode))
    }else {
        node.right === null ? (node.right = newNode) : (insertNode(node.right, newNode))
    }
}

这里我们用到递归，接下来要实现的search，del等都会大量使用递归，所以说不了解的可以先自行学习了解。我们创建一个二叉树实例，来插入一个键：

let tree = new BinarySearchTree();
tree.insert(20);
tree.insert(21);
tree.insert(520);
tree.insert(521);

树的遍历

• 中序遍历：以从最小到最大的顺序访问所有节点
• 先序遍历：以优先于后代节点的顺序访问每个节点
• 后序遍历：先访问节点的后代节点再访问节点本身

1. 中序排序

this.inOrderTraverse = function(cb){
    inOrderTraverseNode(root, cb);
}

// 辅助函数
function inOrderTraverseNode(node, cb){
    if(node !== null){
        inOrderTraverseNode(node.left, cb);
        cb(node.key);
        inOrderTraverseNode(node.right, cb);
    }
}

2. 先序排序

// 先序排序 --- 优先于后代节点的顺序访问每个节点
   this.preOrderTraverse = function(cb) {
     preOrderTraverseNode(root, cb);
   }

   // 先序排序辅助方法
   function preOrderTraverseNode(node, cb) {
     if(node !== null) {
       cb(node.key);
       preOrderTraverseNode(node.left, cb);
       preOrderTraverseNode(node.right, cb);
     }
   }

3. 后序排序

// 后续遍历 --- 先访问后代节点，再访问节点本身
   this.postOrderTraverse = function(cb) {
     postOrderTraverseNode(root, cb);
   }

   // 后续遍历辅助方法
   function postOrderTraverseNode(node, cb) {
     if(node !== null){
       postOrderTraverseNode(node.left, cb);
       postOrderTraverseNode(node.right, cb);
       cb(node.key);
     }
   }

搜索树中的值

1. 最小值

// 最小值
   this.min = function(){
     return minNode(root)
   }

    function minNode(node) {
     if(node) {
       while(node && node.left !== null){
         node = node.left;
       }
       return node.key
     }
     return null
   }

// 最大值
   this.max = function() {
     return maxNode(root)
   }

   function maxNode(node) {
     if(node){
       while(node && node.right !== null){
         node = node.right;
       }
       return node.key
     }
     return null
   }

// 搜索树中某个值
this.search = function(key) {
    return searchNode(root, key)
}

// 搜索辅助方法
function searchNode(node, key){
    if(node === null) {
        return false
    }
    if(key < node.key) {
        return searchNode(node.left, key)
    } else if(key > node.key) {
        return searchNode(node.right, key)
    }else {
        return true
    }
}

3. 移除一个节点

this.remove = function(key){
    root = removeNode(root, key);
}

// 发现最小节点
function findMinNode(node) {
    if(node) {
    while(node && node.left !== null){
        node = node.left;
    }
    return node
    }
    return null
}

// 移除节点辅助方法
function removeNode(node, key) {
    if(node === null) {
    return null
    }

    if(key < node.key){
    node.left = removeNode(node.left, key);
    return node
    } else if( key > node.key){
    node.right = removeNode(node.right, key);
    return node
    } else {
    // 一个页节点
    if(node.left === null && node.right === null) {
        node = null;
        return node
    }

    // 只有一个子节点的节点
    if(node.left === null) {
        node = node.right;
        return node
    }else if(node.right === null) {
        node = node.left;
        return node
    }

    // 有两个子节点的节点
    let aux = findMinNode(node.right);
    node.key = aux.key;
    node.right = removeNode(node.right, aux.key);
    return node
    }
}

删除节点需要考虑的情况比较多，这里我们会使用和min类似的实现去写一个发现最小节点的函数，当要删除的节点有两个子节点时，我们要将当前要删除的节点替换为子节点中最大的一个节点的值，然后将这个子节点删除。

至此，一个二叉搜索树已经实现，但是还存在一个问题，如果树的一遍非常深，将会存在一定的性能问题，为了解决这个问题，我们可以利用AVL树，一种自平衡二叉树，也就是说任何一个节点的左右两侧子树的高度之差最多为1。

如果想学习更多js算法和数据结构，可以继续观看哦~

点个在看，你最好看