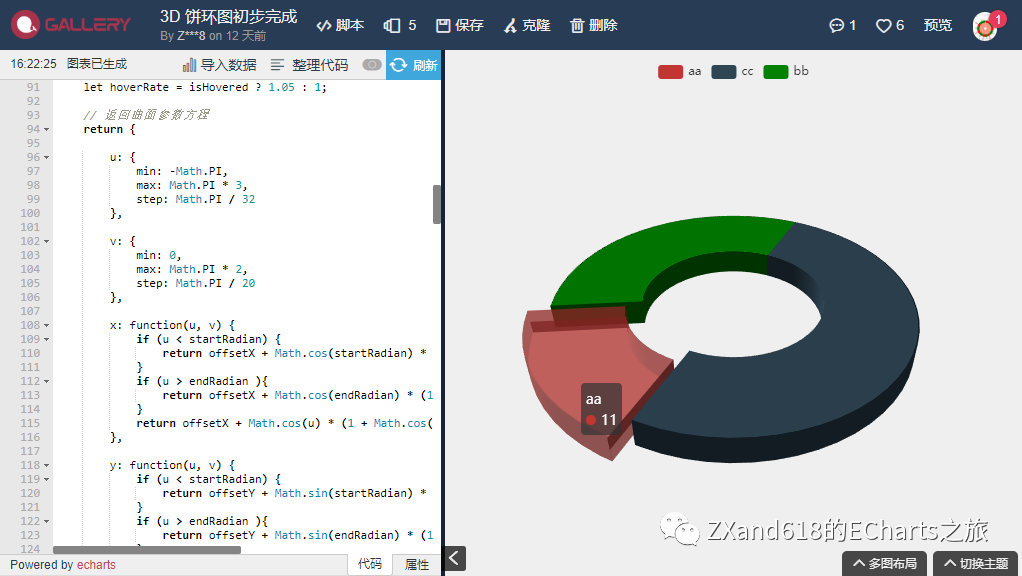
饼环最终效果

前些天有读者想做 3D 饼环图，问如何实现。

我顺着自己 3D 饼图（ECharts 3D 饼图近似实现）的思路想了想，发现这条路不好走……

 

正发愁中，突然想到了一个新思路：之前不是把一个球拍扁再切分得到了 3D 饼图么，那我这次可以把一个类似手镯的东西拍扁（又来了）再切分啊~

 

 

饼环图的思路

 

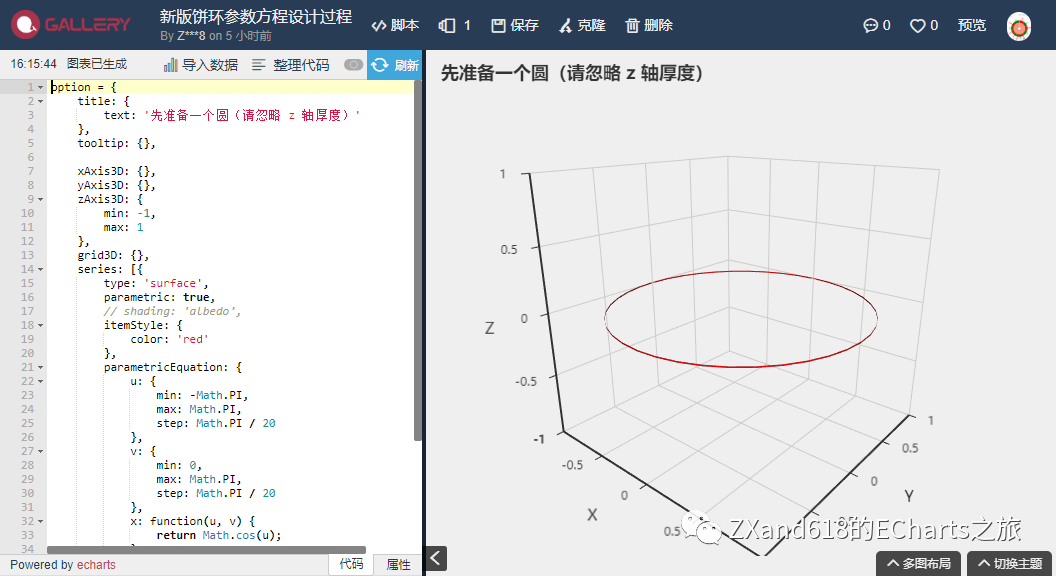
1、为了得到一个『手镯』，先准备了一个圆（参考了圆的参数方程）

圆的参数方程 x=a+r cosθ y=b+r sinθ（θ∈ [0，2π) ） (a,b) 为圆心坐标，r 为圆半径，θ 为参数，(x,y) 为经过点的坐标

https://baike.baidu.com/item/%E5%8F%82%E6%95%B0%E6%96%B9%E7%A8%8B

先准备一个圆（请忽略 z 轴厚度）

【红色圆的参数方程】

x: cosA

y: sinA

角度参数 A

-------------

为了能看到这个用参数曲面绘制的圆，只好给其增加加厚度（变成圆柱）

z: sinB > 0 ? h : -h

角度参数 B，固定值 r < 1， 固定值 h。

 

 

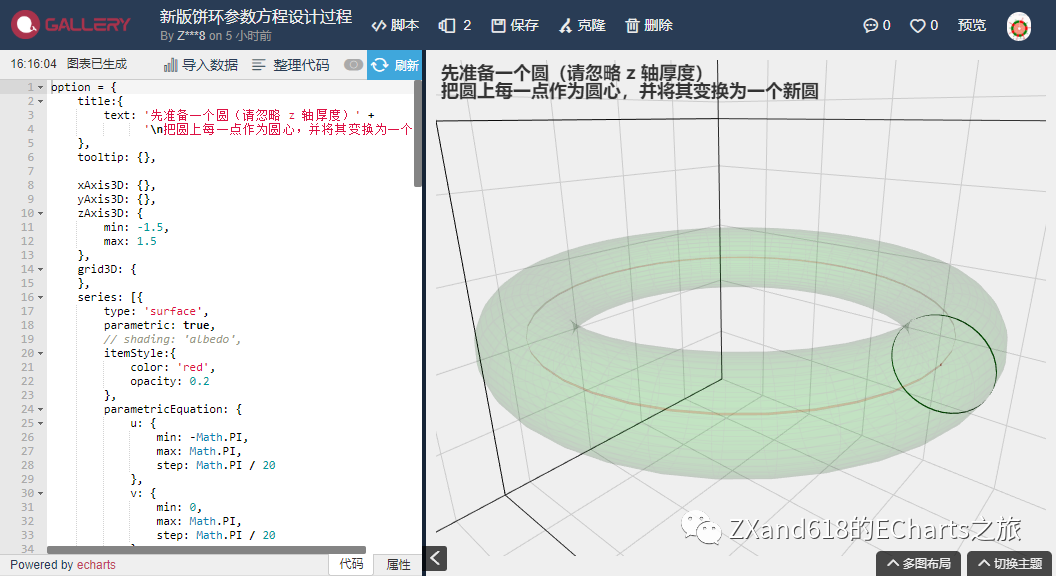
2、将圆上每一个点，都变换成一个以该点为圆心的新圆（如下图所示）

把圆上每一点作为圆心，并将其变换为一个新圆，无数新圆组成我们要的『手镯』

【绿色部分的参数方程】

x: cosA * (1 + r * cosB)

y: sinA * (1 + r * sinB)

z: r * sinB

角度参数 A，角度参数 B，固定值 r < 1，r 为新圆半径（为方便，旧圆半径等于 1）

 

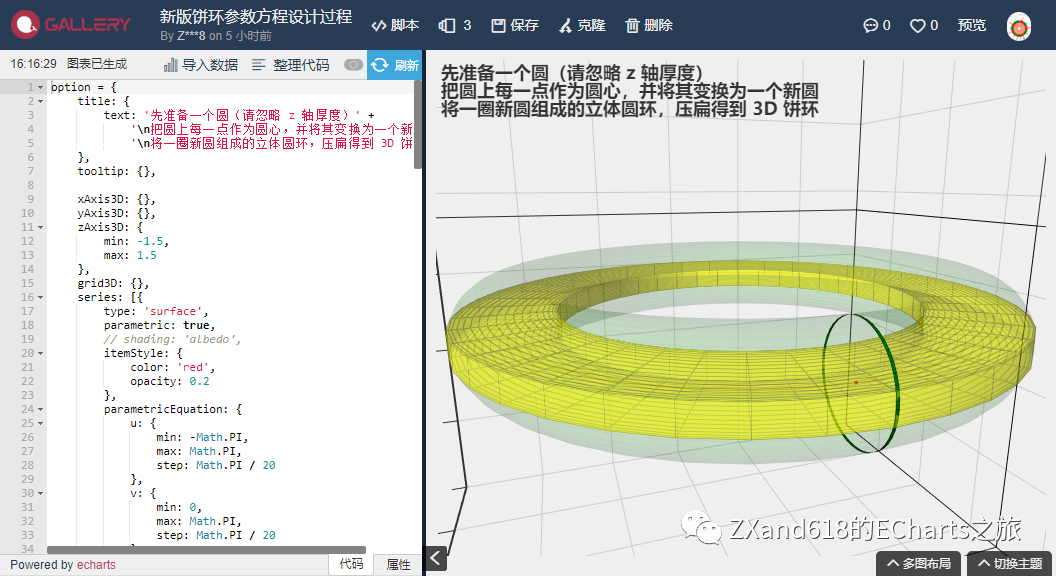
3、将『手镯』拍扁……得到 3D 饼环

将一圈新圆组成的立体圆环，压扁得到 3D 饼环（黄色）

【黄色部分的参数方程】

x: cosA * (1 + r * cosB)

y: sinA * (1 + r * sinB)

z: r * sinB > 0 ? h : -h

角度参数 A，角度参数 B，固定值 r < 1， 固定值 h 为饼环厚度

 

 

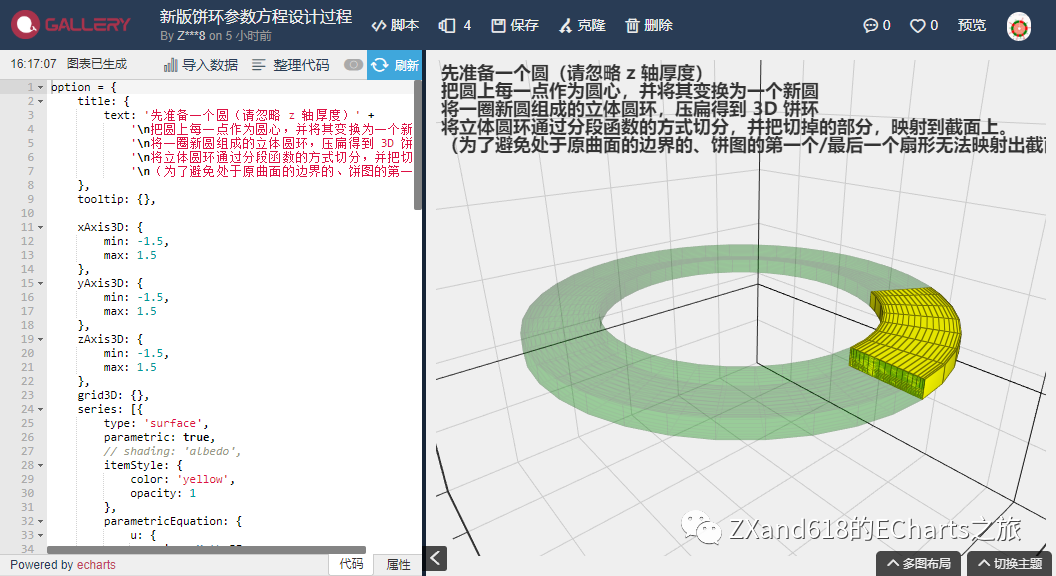
4、将立体圆环通过分段函数的方式切分，并把切掉的部分，映射到截面上。为了避免处于原曲面的边界的、饼图的第一个/最后一个扇形无法映射出截面，需要增加其中一个输入参数的取值范围。

将 3D 饼环中不需要的部分，映射到切分截面『封口』

这部分的参数方程比较繁琐，具体见代码吧……

大体思路就是对角度参数 A 进行判断（分段函数），如果 A < 切分的起始角度，则按照切分的起始角度计算坐标值，如果 A > 切分的终止角度，则按照切分的终止角度计算坐标值，并使其分布在截面上。

 

 

饼环图的实现

 

实现方面，与之前的「ECharts 3D 饼图近似实现」大致相同，基本上就改了参数方程，加了一个内外径比例的参数。

 

【一】定义一个函数，用于获得特定比例扇形的参数方程，其输入参数包括：

 

1. startRatio（浮点数）: 当前扇形起始比例，取值区间 [0, endRatio)

2. endRatio（浮点数）: 当前扇形结束比例，取值区间 (startRatio, 1]

3. isSelected（布尔值）:是否选中，效果参照二维饼图选中效果（单选）

4. isHovered（布尔值）: 是否放大，效果接近二维饼图高亮（放大）效果（未能实现阴影）

5. k（0~1之间的浮点数）：用于参数方程的一个参数，其实就是前面的「新圆」半径与「旧圆」半径的比值，取值在 0~1 之间，通过「内径/外径」的值换算而来。

 

// 生成扇形的曲面参数方程，用于 series-surface.parametricEquationfunction getParametricEquation(startRatio, endRatio, isSelected, isHovered, k) {
    // 计算    let midRatio = (startRatio + endRatio) / 2;
    let startRadian = startRatio * Math.PI * 2;    let endRadian = endRatio * Math.PI * 2;    let midRadian = midRatio * Math.PI * 2;
    // 如果只有一个扇形，则不实现选中效果。    if (startRatio === 0 && endRatio === 1) {        isSelected = false;    }        // 通过扇形内径/外径的值，换算出辅助参数 k（默认值 1/3）    k = typeof k !== 'undefined' ? k : 1 / 3 ;        // 计算选中效果分别在 x 轴、y 轴方向上的位移（未选中，则位移均为 0）    let offsetX = isSelected ? Math.cos(midRadian) * 0.1 : 0;    let offsetY = isSelected ? Math.sin(midRadian) * 0.1 : 0;
    // 计算高亮效果的放大比例（未高亮，则比例为 1）    let hoverRate = isHovered ? 1.05 : 1;
    // 返回曲面参数方程    return {
        u: {            min: -Math.PI,            max: Math.PI * 3,            step: Math.PI / 32        },                v: {            min: 0,            max: Math.PI * 2,            step: Math.PI / 20        },                x: function(u, v) {            if (u < startRadian) {                return offsetX + Math.cos(startRadian) * (1 + Math.cos(v) * k) * hoverRate;            }            if (u > endRadian ){                return offsetX + Math.cos(endRadian) * (1 + Math.cos(v) * k) * hoverRate;            }            return offsetX + Math.cos(u) * (1 + Math.cos(v) * k) * hoverRate;        },                y: function(u, v) {            if (u < startRadian) {                return offsetY + Math.sin(startRadian) * (1 + Math.cos(v) * k) * hoverRate;            }            if (u > endRadian ){                return offsetY + Math.sin(endRadian) * (1 + Math.cos(v) * k) * hoverRate;            }            return offsetY + Math.sin(u) * (1 + Math.cos(v) * k) * hoverRate;        },                z: function(u, v) {            if (u < - Math.PI * 0.5 ) {                return Math.sin(u);            }            if (u > Math.PI * 2.5 ){                return Math.sin(u);            }            return Math.sin(v) > 0 ? 1 : -1;        }    };}

 

【二】再定义一个：传入饼图数据、内径/外径的值，生成模拟 3D 饼图的配置项的函数。

 

1. pieData（object）：饼图数据

2. internalDiameterRatio（0~1之间的浮点数）：内径/外径的值（默认值 1/2），当该值等于 0 时，为普通饼图

 

备注：饼图数据格式示意如下

[{    name: '数据1',    value: 10}, {    // 数据项名称    name: '数据2',    value: 56,    itemStyle: {        // 透明度        opacity: 0.5,        // 扇形颜色        color: 'green'    }}]

 

函数定义如下：

// 生成模拟 3D 饼图的配置项function getPie3D(pieData, internalDiameterRatio) {
    let series = [];    let sumValue = 0;    let startValue = 0;    let endValue = 0;    let legendData = [];    let k = typeof internalDiameterRatio !== 'undefined' ? (1 - internalDiameterRatio) / (1 + internalDiameterRatio): 1 / 3;
    // 为每一个饼图数据，生成一个 series-surface 配置    for (let i = 0; i < pieData.length; i++) {
        sumValue += pieData[i].value;
        let seriesItem = {            name: typeof pieData[i].name === 'undefined' ? `series${i}` : pieData[i].name,            type: 'surface',            parametric: true,            wireframe: {                show: false            },            pieData: pieData[i],            pieStatus: {                selected: false,                hovered: false,                k: k            }        };
        if (typeof pieData[i].itemStyle != 'undefined') {
            let itemStyle = {};
            typeof pieData[i].itemStyle.color != 'undefined' ? itemStyle.color = pieData[i].itemStyle.color : null;            typeof pieData[i].itemStyle.opacity != 'undefined' ? itemStyle.opacity = pieData[i].itemStyle.opacity : null;
            seriesItem.itemStyle = itemStyle;        }        series.push(seriesItem);    }
    // 使用上一次遍历时，计算出的数据和 sumValue，调用 getParametricEquation 函数，    // 向每个 series-surface 传入不同的参数方程 series-surface.parametricEquation，也就是实现每一个扇形。    for (let i = 0; i < series.length; i++) {        endValue = startValue + series[i].pieData.value;
        series[i].pieData.startRatio = startValue / sumValue;        series[i].pieData.endRatio = endValue / sumValue;        series[i].parametricEquation = getParametricEquation(series[i].pieData.startRatio, series[i].pieData.endRatio, false, false, k);
        startValue = endValue;
        legendData.push(series[i].name);    }
    // 补充一个透明的圆环，用于支撑高亮功能的近似实现。    series.push({        name: 'mouseoutSeries',        type: 'surface',        parametric: true,        wireframe: {            show: false        },        itemStyle: {            opacity: 0        },        parametricEquation: {            u: {                min: 0,                max: Math.PI * 2,                step: Math.PI / 20            },            v: {                min: 0,                max: Math.PI,                step: Math.PI / 20            },            x: function(u, v) {                return Math.sin(v) * Math.sin(u) + Math.sin(u);            },            y: function(u, v) {                return Math.sin(v) * Math.cos(u) + Math.cos(u);            },            z: function(u, v) {                return Math.cos(v) > 0 ? 0.1 : -0.1;            }        }    });
    // 准备待返回的配置项，把准备好的 legendData、series 传入。    let option = {        //animation: false,        legend: {            data: legendData        },        tooltip: {            formatter: params => {                if (params.seriesName !== 'mouseoutSeries') {                    return `${params.seriesName}<br/><span style="display:inline-block;margin-right:5px;border-radius:10px;width:10px;height:10px;background-color:${params.color};"></span>${option.series[params.seriesIndex].pieData.value}`;                }            }        },        xAxis3D: {            min: -1,            max: 1        },        yAxis3D: {            min: -1,            max: 1        },        zAxis3D: {            min: -1,            max: 1        },        grid3D: {            show: false,            boxHeight: 10,            //top: '30%',            bottom: '50%'        },        series: series    };    return option;}

 

函数的流程大致是：

1. 首次遍历传入的数据，为每一个数据项。准备对应的系列（series-surface）基础配置，存入列表「series」中，并计算数据值的总和 sumValue；

2. 遍历列表「series」，为每一个系列补充对应的参数方程「series-surface.parametricEquation」，并在系列配置中记录生成参数方程所用的原始参数，startRatio、endRatio 等（isSelected、isHovered、k 在首次遍历时，已记录在 series-surface.pieStatus 中，其中前两个为默认值 false，k 根据是否传入 internalDiameterRatio 而定）

3. 在列表「series」末尾追加一个透明的辅助系列，包在 3D 饼图周围，相当于一个「围栏」，用于判断鼠标是否移出饼图范围。

4. 使用准备好的 series，组成完整的配置项 option，作为函数返回值。

 

 

【三】监听鼠标点击事件，实现饼图选中效果（单选）

主要就是先读取被点击扇形当前的状态，再调用函数「getParametricEquation」更新其参数方程，最后更新图表。

 

【四】结合辅助『围栏』，监听 mouseover 和 globalout 事件，近似实现高亮（放大）效果。

• 大致思路是，在饼图外部套一层透明的圆环，然后监听 mouseover 事件，获取到对应数据的系列序号 params.seriesIndex 或系列名称 params.seriesName，如果鼠标移到了扇形上，则先取消高亮之前的扇形（如果有）,再高亮当前扇形；如果鼠标移到了透明圆环上，则只取消高亮之前的扇形（如果有），不做任何高亮。

• 当鼠标移动过快，直接划出图表区域时，有可能监听不到透明圆环的 mouseover，导致此前高亮没能取消，所以补充了对 globalout 的监听。

 

【备注】

1. 前面【三】和【四】与「ECharts 3D 饼图近似实现」相比，就是多了一个参数 k（「新圆」半径与「旧圆」半径的比值），变化不大，所以没有贴具体代码；

2. internalDiameterRatio 等于 0，也就是 k 等于 1 时，可实现普通 3D 饼图（非饼环）。

 

 

 

👇阅读原文查看 ECharts Gallery 例子