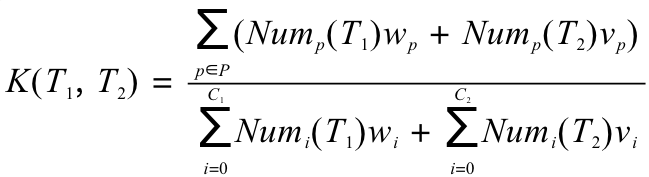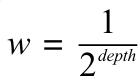本文最初发布于KFive Team公众号,原始链接:https://mp.weixin.qq.com/s/mNfsPxdwsiHMkb65AcS8dA
在开始本文的论述之前,先讲一些背景知识。
百度搜索结果由一个个卡片构成,所有卡片都是独立开发维护的代码模块。由于历史积累导致这些卡片数量庞大(2000+),存在很多重复或者相似的卡片。这些卡片会严重拖累搜索整体的迭代效率,并且给卡片管理和维护增加了很多成本。所以我们想要对所有卡片统一梳理,希望能做到卡片的收敛和归一,减轻历史包袱,轻装上阵。
由于卡片数量庞大,一个一个人工确认显然是不现实的,怎么才能更高效地开展这项工作是一个棘手的问题。
目前搜索卡片都采用了组件化的开发方式,那么每个卡片的结构其实可以用一个组件树的结构来表示。我们的思路就是对这些组件树进行相似度分析,最后将相似度高的组件树归为一类,那么这一类相似度高的模板就是可以复用和归一化的。接下来具体介绍一下实现方法。
卡片相似度计算
卡片解析成组件树
借助编译工具或者框架本身提供的 compiler 方法,可以很容易的将卡片template代码转化为 AST 数据,AST 本身就是一个树形结构。我们拿一个卡片 A 举例,卡片 A 对应的 AST 对象如下所示:
{
type: 1,
tag: 'c-aladdin',
attrsList:
[ { name: ':title', value: 'title' },
{ name: 'url', value: 'javascript:void(0)' },
{ name: 'hide-footer', value: '' },
{ name: '@title-click', value: 'toggleTab' },
{ name: 'title-arrow', value: '' },
{ name: 'title-feedback', value: '' } ],
attrsMap:
{ ':title': 'title',
url: 'javascript:void(0)',
'hide-footer': '',
'@title-click': 'toggleTab',
'title-arrow': '',
'title-feedback': '' },
parent: undefined,
children:
[ { type: 1,
tag: 'c-scroll',
attrsList: [Array],
attrsMap: [Object],
parent: [Circular],
children: [Array],
plain: false,
hasBindings: true,
events: [Object] } ],
plain: false,
hasBindings: true,
attrs:
[ { name: 'title', value: 'title' },
{ name: 'url', value: '"javascript:void(0)"' },
{ name: 'hide-footer', value: '""' },
{ name: 'title-arrow', value: '""' },
{ name: 'title-feedback', value: '""' } ],
events:
{ 'title-click': { value: 'toggleTab', modifiers: undefined } }
}
这个AST树节点上存在很多属性,包括tag/attrsList/parent/children/events等,我们为了计算方便,这里去掉一些属性,只保留tag/children等少数属性。另外加上节点的id和层级信息等,最终生成的模板组件树结构如下:
{
"name": "ly_viewport_scene",
"root": {
"depth": 1,
"id": 1,
"name": "c-aladdin",
"children": [
{
"depth": 2,
"id": 2,
"name": "c-scroll",
"children": [
{
"depth": 3,
"id": 3,
"name": "c-scroll-item",
"children": [
{
"depth": 4,
"id": 4,
"name": "c-link",
"children": [
{
"depth": 5,
"id": 5,
"name": "div",
"children": [
{
"depth": 6,
"id": 6,
"name": "c-image"
},
{
"depth": 6,
"id": 7,
"name": "c-label"
}
]
},
{
"depth": 5,
"id": 6,
"name": "c-line",
"children": []
}
]
}
]
},
{
"depth": 3,
"id": 4,
"name": "c-scroll-item",
"children": [
{
"depth": 4,
"id": 5,
"name": "c-more"
}
]
}
]
}
]
}
}
最终我们可以拿到所有卡片的组件树结构信息。
组件树的相似度计算
那么两个卡片对应的组件树的相似度怎么计算呢?目前有几种主流的思路:
- 基于树编辑距离的相似度计算:编辑距离指的是把树 T1 转化成树 T2 的最小代价,包括替换节点、插入节点、删除节点的代价。代价越小,编辑距离越短,说明两棵树越相似。
- 基于公共子路径的相似度计算:分别计算出树 T1 和 T2 所有子路径,在树 T1 和 T2 中都出现过的公共子路径越多,说明两棵树越相似。
- 基于公共子字符串的相似度计算:将树结构转换为前序遍历(或其它遍历方式)得到的由节点名组成的字符串 S1 和 S2 ,然后计算 S1 和 S2 的公共子串的长度和个数,数值越大说明两棵树越相似。
- 基于同层子节点匹配的相似度计算:对应树 T1 和 T2 的每一层节点,使用动态规划算法得到最相似节点,在最相似节点上继续进行匹配,其它节点则产生差异值,最后得到汇总的差异值越小,两棵树越相似。
- 基于同构特征的相似度计算:构造出 K 个节点的所有非同构形态子树,然后计算树 T 中这些子树的同构个数,将其作为特征向量,最后通过计算两组特征向量来计算两棵树的相似度。
下面重点介绍一下我所采用的方法 2 - 基于公共子路径的相似度计算方法。
基于公共子路径的相似度计算方法
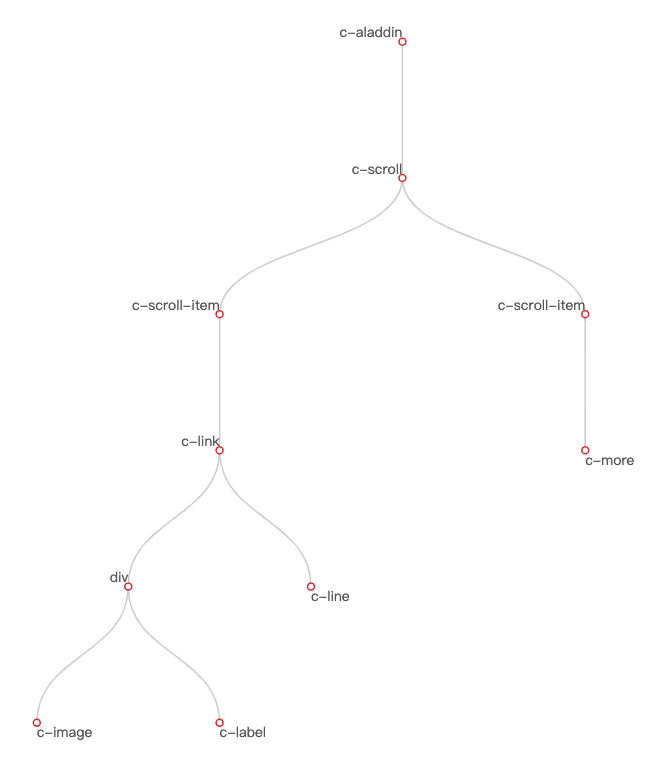
规定树的一条路径是从根节点到叶子节点这条线上所有节点组成的一条路径,子路径就是这条路径上截取任意一段得到的路径。还是卡片 A 为例,对上面的组件树对象可视化得到:
![]()
计算组件树子路径的方法如下:
/**
* 计算一个模板组件树的所有子路径
*
* @param tree 模板组件树
* @return 添加了 depth 和 subPaths 的模板组件树
*/
export function getSubPathsFromTree(tree: ITree): ITree {
const subPaths = {};
const maxDepth = -1;
if (tree.root) {
deepTraverse(tree.root, [], subPaths, [], maxDepth);
tree.depth = maxDepth;
tree.subPaths = subPaths;
}
return tree;
}
/**
* 深度遍历组件树
*
* @param root 当前遍历到的节点
* @param rootPath 从根节点到当前节点的路径
* @param subPaths 所有子路径
* @param track 保存统计过的节点 id 构成的子路径(形如'0/1/3'),避免重复统计
* @param maxDepth 计算组件树的深度
*/
function deepTraverse(
root: INode,
rootPath: IRootPathNode[],
subPaths: ISubPath,
track: string[],
maxDepth: number
): void {
const { id, tag, depth, children } = root;
if (maxDepth < depth) {
maxDepth = depth;
}
const newPath = rootPath.concat([{ id, tag, depth }]);
if (!children || !children.length) {
generateSubPath(newPath, 1, subPaths, track);
} else {
for (const node of children) {
deepTraverse(node, newPath, subPaths, track, maxDepth);
}
}
}
/**
* 计算一条从根节点到叶子节点的路径的所有子路径
*
* @param rootPath 从根节点到当前节点的路径
* @param len 当前需要生成子路径的长度
* @param subPaths 所有子路径
* @param track 保存统计过的节点 id 构成的子路径(形如'0/1/3'),避免重复统计
*/
function generateSubPath(
rootPath: IRootPathNode[],
len: number,
subPaths: ISubPath,
track: string[]
) {
for (let i = 0; i + len - 1 < rootPath.length; i++) {
const curPath = rootPath.slice(i, i + len);
const depth = curPath[0].depth;
const idKey = curPath.map(item => item.id).join("/");
const tagKey = curPath.map(item => item.tag).join("/");
if (track.indexOf(idKey) === -1) {
track.push(idKey);
if (subPaths[tagKey]) {
subPaths[tagKey].count += 1;
} else {
subPaths[tagKey] = {
count: 1,
depth
};
}
}
}
if (len < rootPath.length) {
generateSubPath(rootPath, len + 1, subPaths, track);
}
}
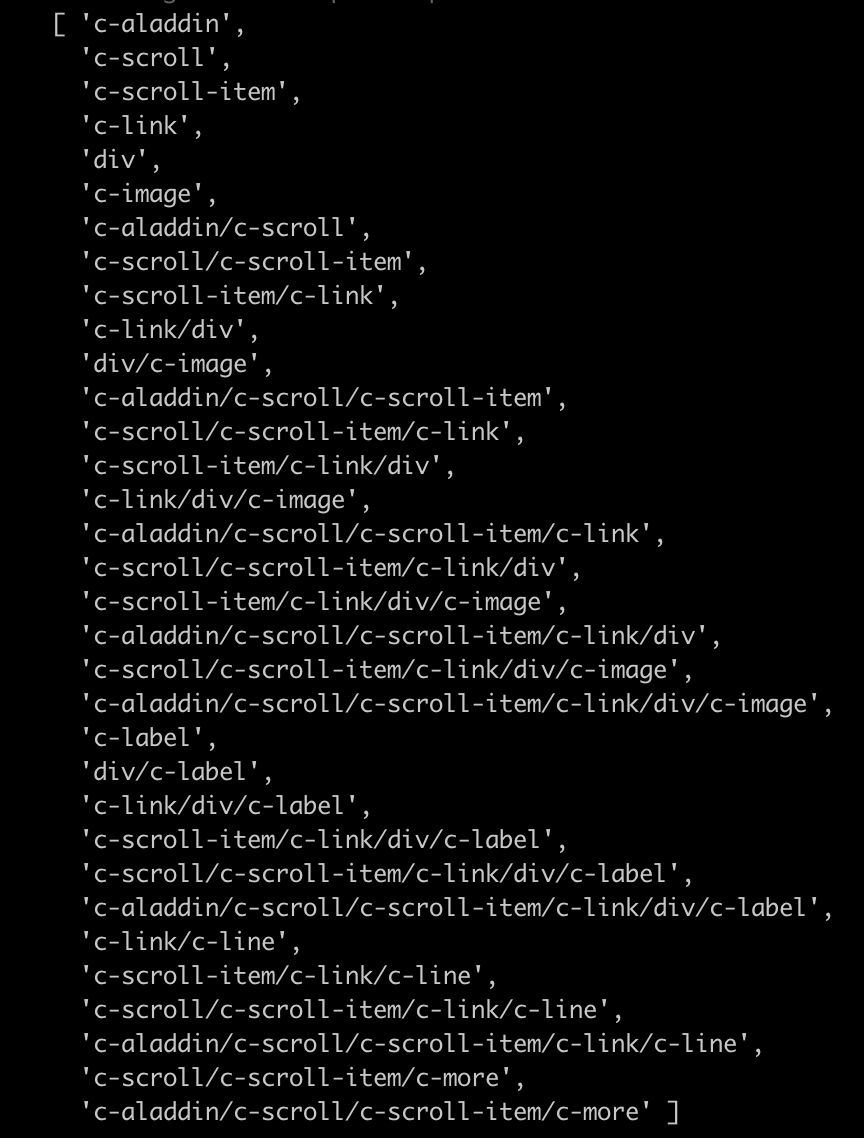
通过计算得出它的所有子路径共 33 个,如下:
![]()
我们可以知道,如果 T1 和 T2 中的相同子路径数越多,说明 T1 和 T2 越相似。另外,还会发现相似的树中不一致的区块往往出现在树中层次较深的位置。因此,可以设计出计算相似度的公式:
![]()
其中 Nump(T) 表示子路径 p 在树 T 中出现的次数,P 表示在树 T1 和 T2 中一共有的子路径集合,C1 和 C2 分别对应树 T1 和 T2 各自的子路径集合,wp 和 vp 分别对应树 T1 和 T2 中子路径 p 的权重参数。这个权重参数由子路径的深度决定,子路径的深度规定为子路径中第一个节点的深度。子路径越深,权重参数应该越小,权重参数的计算公式如下:
![]()
这样计算出来的相似度数值可以在很大程度上反映两个组件树的相似程度,如果两个树越相似,那么这个相似度数值就会越大。最大值是 1,表明两个树完全相同(包括所有节点信息和结构信息),最小值是 0,表明两个树没有任何相似点。
计算两个组件树相似度的方法如下:
/**
* 计算两个组件树的相似度值
*
* @param tree1 第一个组件树
* @param tree2 第二个组件树
* @return 相似度值。范围0~1,0表示完全不同,1表示完全相同
*/
export default function calcSimilarityBySubPath(tree1: ITree, tree2: ITree): number {
const { depth: depth1, subPaths: subPaths1 } = getSubPathsFromTree(tree1);
const { depth: depth2, subPaths: subPaths2 } = getSubPathsFromTree(tree2);
const commonSubPath = [];
const allSubPathSet = new Set();
Object.keys(subPaths1).forEach(subPath => {
allSubPathSet.add(subPath);
if (subPaths2[subPath]) {
commonSubPath.push(subPath);
}
});
Object.keys(subPaths2).forEach(subPath => allSubPathSet.add(subPath));
// key: subPath, value: weight
const allSubPath: ISubPathWeight = Array.from(allSubPathSet).reduce(
(acc, key) => {
const weight1 = calcWeight(
depth1,
subPaths1[key] && subPaths1[key].depth
);
const weight2 = calcWeight(
depth2,
subPaths2[key] && subPaths2[key].depth
);
acc[key] = [weight1, weight2];
return acc;
},
{}
);
const value = Object.keys(allSubPath).reduce(
(acc, key) => {
if (allSubPath[key][0] && allSubPath[key][1]) {
const curValue =
allSubPath[key][0] * subPaths1[key].count +
allSubPath[key][1] * subPaths2[key].count;
acc.simValue += curValue;
acc.totalValue += curValue;
} else if (allSubPath[key][0]) {
acc.totalValue += allSubPath[key][0] * subPaths1[key].count;
} else if (allSubPath[key][1]) {
acc.totalValue += allSubPath[key][1] * subPaths2[key].count;
}
return acc;
},
{
simValue: 0,
totalValue: 0
}
);
const kernelValue = Number(Number(value.simValue / value.totalValue).toFixed(2));
return kernelValue;
}
示例
根据上面的相似度计算方法,我们选取两个卡片(卡片 A 和卡片 B),计算出这两个卡片之间的相似度为 0.71。
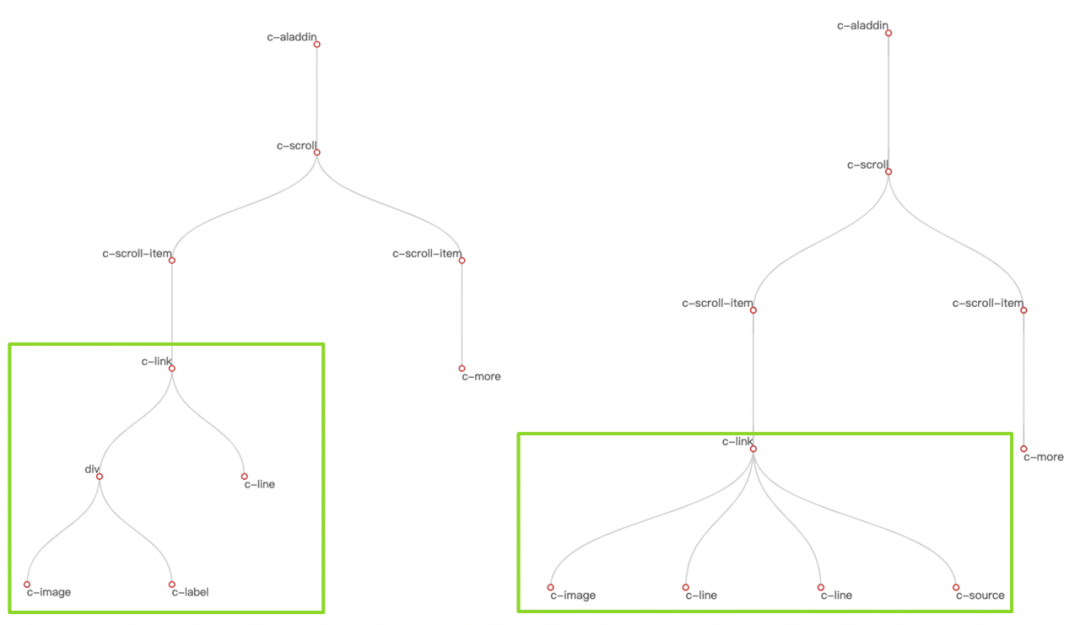
组件树对比:
![]()
两个树整体结构相似,只是在局部区块c-link节点下的子节点结构有所不同。
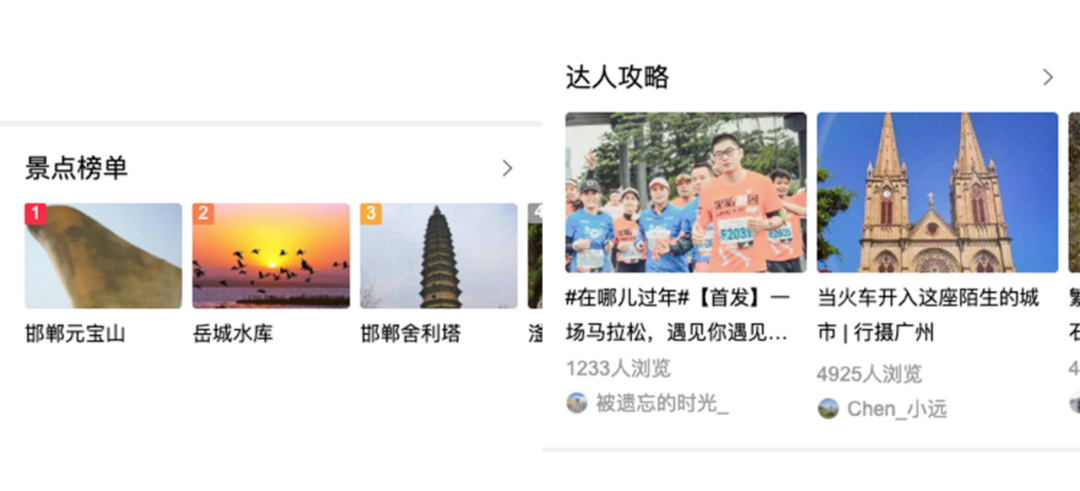
模板线上样式对比:
![]()
我们看这两个卡片真正在线上展现的样子,可以看到都是只包含了标题组件和横滑组件的卡片,只是横滑内部每个单元的元素有些不一样。所以 0.71 还是可以比较好的反映这两个卡片的相似度。
卡片分类和归一
对卡片进行分类是指,相似度越高的卡片应该被归为一类。但是目前我们也不确定能将这些卡片分为多少类,每个分类结果中也不确定会包含多少个卡片。
这个问题可以使用聚类分析的方法解决,属于典型的机器学习中的无监督学习。即从没有标注的数据中分析数据的特征,得到的分类结果是不确定的。对应的机器学习中还有一种类型叫作监督学习,即依赖于从预先标注的数据中学习到如何对数据特征进行判断和归类,然后才可以对未知数据进行预测。
常见的聚类分析算法有以下几种:
- K-Means 均值聚类
- 层次聚类
- 基于密度的聚类
- 基于网格的聚类
我选择了相对简单的层次聚类方法来做分析。
聚类分析过程
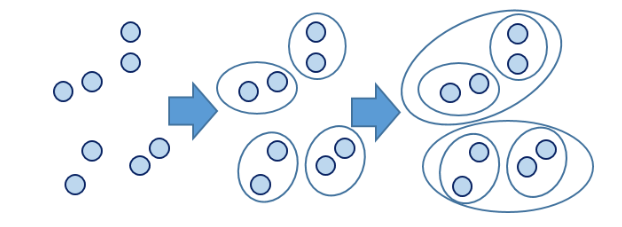
层次聚类算法的主要流程是,把每一个样本数据都视为一个类,然后计算各类之间的距离,选取最相近的两个类,将它们合并为一个类。新的这些类再继续计算距离,合并距离最近的两个类。如此往复,如果没有终止条件判断,最后就会合并成只有一个类。它是一个自底向上的构建一颗有层次的嵌套聚类树的过程。
![]()
各类之间的距离在目前讨论的场景中就是卡片之间的相似度值。根据上面的计算组件树相似度的方法,我们对所有卡片进行两两计算,得到一个包含所有卡片相似度的矩阵。接下来就是基于这个相似度矩阵的计算。
计算步骤如下:
- 基于相似度矩阵,选取相似度值最大的两个卡片,把这两个卡片合并为一类
- 然后更新相似度矩阵:计算新合并类与其它类的距离(相似度),将新合并生成的类加入到矩阵中,删除合并之前的子类
- 然后基于更新后的相似度矩阵,迭代重复上述步骤,直到满足终止条件时停止
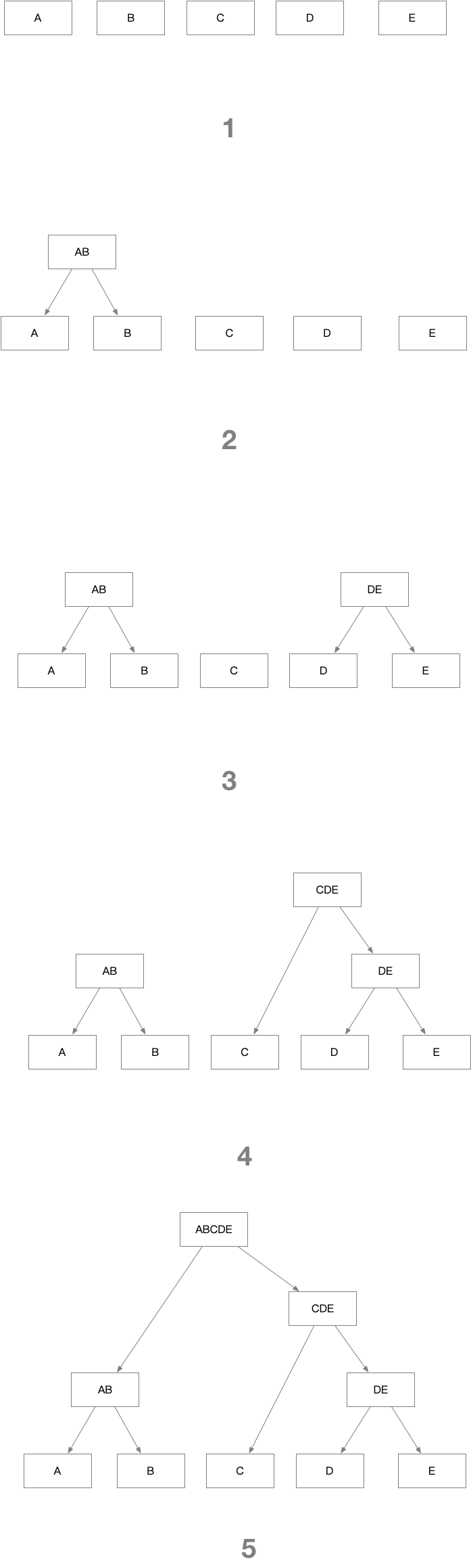
假设我们有 5 个卡片A/B/C/D/E,聚类的简易流程如下图所示:
![]()
具体的聚类计算过程如下:
/**
* 聚类算法
*
* @param nodes 所有节点结构化信息
* @param matrix 相似度矩阵
* @param options 聚类参数
*/
function cluster(
nodes: IClusterNodes,
matrix: IMatrix,
options: IClusterOptions
): void {
const matrixOnlyAdd = clone(matrix);
if (!options.thresholdCount) {
options.thresholdCount = 100;
}
if (!options.thresholdSimilarity) {
options.thresholdSimilarity = 1;
}
while (Object.keys(nodes).length > options.thresholdCount) {
const maxEdge = getMaxEdge(matrix);
if (maxEdge.value < options.thresholdSimilarity) {
break;
}
// merge nodes and update nodes
const id = uuid.v1();
const node1 = nodes[maxEdge.source];
const node2 = nodes[maxEdge.target];
const simValue = calcSimValue(nodes, maxEdge);
nodes[id] = {
set: node1.set.concat(node2.set),
simValue,
};
delete nodes[maxEdge.source];
delete nodes[maxEdge.target];
// update matrix
matrix[id] = {};
matrixOnlyAdd[id] = {};
for (const key in nodes) {
if (id !== key) {
const distance = calcDistanceByAverage(
nodes[id].set,
matrixOnlyAdd,
key
);
if (distance) {
matrix[id][key] = distance;
matrixOnlyAdd[id][key] = distance;
}
}
}
rmMatrixNodes(matrix, maxEdge.source);
rmMatrixNodes(matrix, maxEdge.target);
}
}
/**
* 计算复合节点添加了 maxEdge 后,形成的新的复合节点的整体相似度,暂以平均值近似计算
*
* @param nodes 所有节点数据
* @param maxEdge 拥有最大相似的边
* @return 新的复合节点的整体相似度
*/
function calcSimValue(nodes: IClusterNodes, maxEdge: IGraphEdge): number {
const node1 = nodes[maxEdge.source];
const node2 = nodes[maxEdge.target];
let simValue;
if (node1.simValue && node2.simValue) {
simValue = (node1.simValue + node2.simValue + maxEdge.value) / 3;
} else if (node1.simValue) {
simValue = (node1.simValue + maxEdge.value) / 2;
} else if (node2.simValue) {
simValue = (node2.simValue + maxEdge.value) / 2;
} else {
simValue = maxEdge.value;
}
return simValue;
}
/**
* 计算节点(聚合)到节点(聚合)的相似度,取节点到聚合节点中的每个节点的相似度平均值
*
* @param list 聚合节点包含的节点列表
* @param matrix 模板相似度矩阵
* @param id 节点 ID
* @return 相似度值
*/
function calcDistanceByAverage(
list: Array<{ id: string; name: string }>,
matrix: IMatrix,
id: string
): number {
let average = 0;
for (const { id: subId } of list) {
average +=
matrix[id] && matrix[id][subId]
? Number(matrix[id][subId])
: matrix[subId][id]
? Number(matrix[subId][id])
: 0;
}
average /= list.length;
return average;
}
这里面还涉及到一些细节问题:
计算聚合节点与其它节点的距离
当合并了两个节点生成一个新的聚合节点时,需要计算新生成的聚合节点到其它所有节点的距离。这里有两种情况:
- 聚合节点到其它单节点(只包含一个卡片)的距离:这种情况下我们采用计算平均值的办法,计算聚合节点中的所有子节点到其它节点的相似度平均值作为距离。
- 聚合节点到其它聚合节点的距离:这种情况下由于聚合节点内部节点到其它聚合节点的距离已经算出,我们依旧可以采用上面的办法。而不是计算两个聚合节点中所有子节点的距离平均值,因为这样计算量会很大,时间复杂度达到
O(n2)。
终止条件的选择
由于聚类分析是一个嵌套迭代的过程。如果没有终止条件,最终聚合成一个类对于模板分析是没有意义的。所以我们需要确定迭代的终止条件。我采用了两种方法:
- 规定一个 分类结果个数阀值:聚类迭代过程中当分类个数小于阀值时终止。这种办法比较简单粗暴,问题是得到最终结果时,我们并不知道每个聚合分类内部的模板相似度情况。
- 规定一个 分类的最低内部相似度阀值:合并模板的时候,我们额外计算一下聚合分类内部的相似度(这个相似度选取分类内部任意两个模板之间相似度的最小值),然后在聚类迭代的过程中判断聚类内部相似度是否小于阀值,如果小于阀值则停止。
模板聚类效果
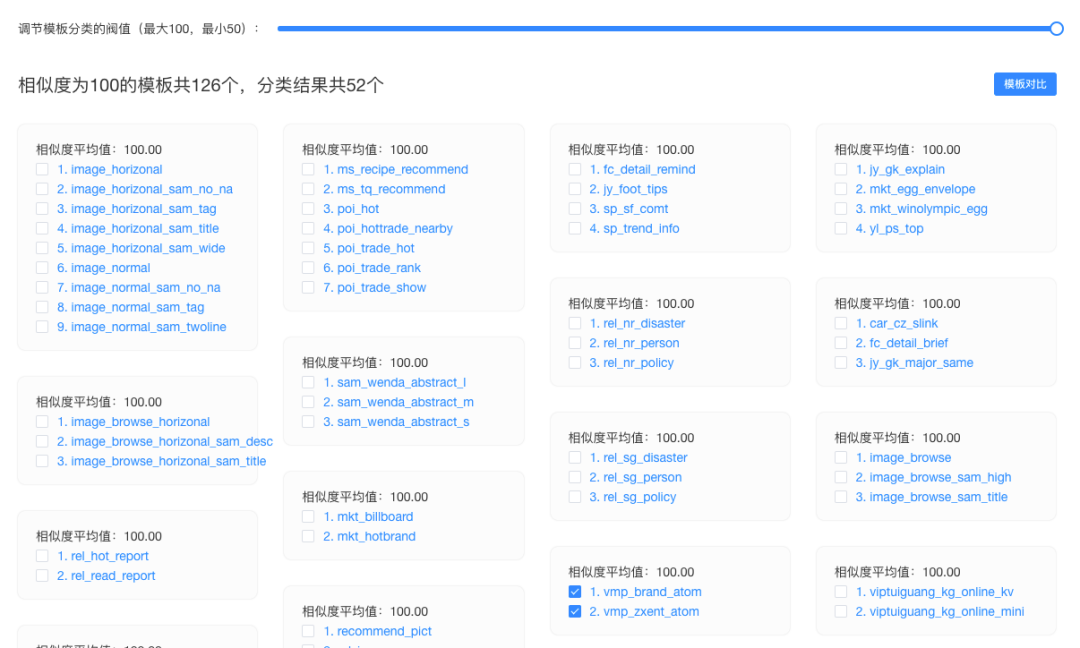
基于上面的模板分析方法,我们最终计算出了卡片归一化的结果。可视化以后的效果如下所示,这里还可以调节相似度阀值查看不同程度的分类结果:
![]()
这里的相似度范围(*100)是 0~100。
待完善的部分
- 生成的组件树仅限于解析卡片的
template部分,并且仅限于静态分析,如果有其它的判断逻辑或者数据处理逻辑,是覆盖不到的,那么卡片还是会有 diff 的。
- 很多看上去相似的卡片,在代码实现上其实是不同的。比如多套了一层
div,或者有隐藏的 DOM 元素,只有在点击交互后才展现等。这种类型的卡片组件树之间的相似度可能会比较小,最终不会被聚类到一起,但其实也属于我们归一化的对象。
- 基于子路径的相似度计算方法,对兄弟节点的顺序不敏感,而对于不同模板而言,即使兄弟节点相同,但是顺序不同,展现上也会有很大的变化。
针对这些不足点,后续还有很大的优化空间。
参考
- Tree Kernels: Quantifying Similarity Among Tree-Structured Data
- 基于 HTML 树的网页结构相似度研究
- 一种基于结构特征的树相似度计算方法
- 层次聚类算法的原理及实现
- 用于数据挖掘的聚类算法有哪些,各有何优势?
- 一篇文章透彻解读聚类分析
作者:姚昌,百度资深前端工程师
更多内容,欢迎关注公众号
![]()