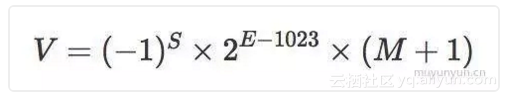探寻 JavaScript 精度问题以及解决方案

阅读完本文可以了解到 0.1+0.2 为什么等于 0.30000000000000004 以及 JavaScript 中最大安全数是如何来的。

十进制小数转为二进制小数方法

拿 173.8125 举例如何将之转化为二进制小数。

① 针对整数部分 173，采取 除2取余，逆序排列。

1. 173 / 2 = 86 ... 1

2. 86 / 2 = 43 ... 0

3. 43 / 2 = 21 ... 1   ↑

4. 21 / 2 = 10 ... 1   | 逆序排列

5. 10 / 2 = 5 ... 0    |

6. 5 / 2 = 2 ... 1     |

7. 2 / 2 = 1 ... 0

8. 1 / 2 = 0 ... 1

得整数部分的二进制为 10101101。

② 针对小数部分 0.8125，采用 乘2取整，顺序排列。

1. 0.8125 * 2 = 1.625  |

2. 0.625 * 2 = 1.25    | 顺序排列

3. 0.25 * 2 = 0.5      |

4. 0.5 * 2 = 1         ↓

得小数部分的二进制为 1101。

③ 将前面两部的结果相加，结果为 10101101.1101。

小心，二进制小数丢失了精度！

根据上面的知识，将十进制小数 0.1 转为二进制：

1. 0.1 * 2 = 0.2

2. 0.2 * 2 = 0.4 // 注意这里

3. 0.4 * 2 = 0.8

4. 0.8 * 2 = 1.6

5. 0.6 * 2 = 1.2

6. 0.2 * 2 = 0.4 // 注意这里，循环开始

7. 0.4 * 2 = 0.8

8. 0.8 * 2 = 1.6

9. 0.6 * 2 = 1.2

10. ...

可以发现有限十进制小数 0.1 却转化成了无限二进制小数 0.00011001100...，可以看到精度在转化过程中丢失了！

能被转化为有限二进制小数的十进制小数的最后一位必然以 5 结尾(因为只有 0.5 * 2 才能变为整数)。所以十进制中一位小数 0.1~0.9 当中除了 0.5 之外的值在转化成二进制的过程中都丢失了精度。

推导 0.1 + 0.2 为何等于 0.30000000000000004

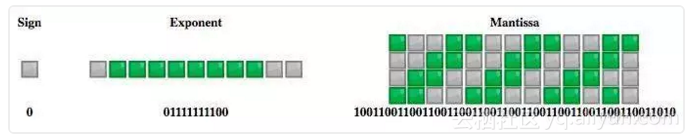
在 JavaScript 中所有数值都以 IEEE-754 标准的 64bit 双精度浮点数进行存储的。先来了解下 IEEE-754 标准下的双精度浮点数。

这幅图很关键，可以从图中看到 IEEE-754 标准下双精度浮点数由三部分组成，分别如下：

• sign(符号): 占 1 bit，表示正负。

• exponent(指数): 占 11 bit，表示范围。

• mantissa(尾数): 占 52 bit，表示精度，多出的末尾如果是 1 需要进位。

推荐阅读 JavaScript 浮点数陷阱及解法，阅读完该文后可以了解到以下公式的由来。

精度位总共是 53 bit，因为用科学计数法表示，所以首位固定的 1 就没有占用空间。即公式中 (M + 1) 里的 1。另外公式里的 1023 是 2^11 的一半。小于 1023 的用来表示小数，大于 1023 的用来表示整数。

指数可以控制到 2^1024 - 1，而精度最大只达到 2^53 - 1，两者相比可以得出 JavaScript 实际可以精确表示的数字其实很少。

0.1 转化为二进制为 0.0001100110011...，用科学计数法表示为 1.100110011...x2^(-4)，根据上述公式， S 为 0(1 bit)， E 为 -4+1023，对应的二进制为 01111111011(11 bit)， M 为 1001100110011001100110011001100110011001100110011010(52 bit，另外注意末尾的进位)， 0.1 的存储示意图如下：

同理， 0.2 转化为二进制为 0.001100110011...，用科学计数法表示为 1.100110011...x2^(-3)，根据上述公式， E 为 -3+1023，对应的二进制为 01111111100, M 为 1001100110011001100110011001100110011001100110011010, 0.2 的存储示意图如下：

0.1+0.2 即 2^(-4) x 1.1001100110011001100110011001100110011001100110011010 与 2^(-3) x 1.1001100110011001100110011001100110011001100110011010 之和

1. // 计算过程

2. 0.00011001100110011001100110011001100110011001100110011010

3. 0.0011001100110011001100110011001100110011001100110011010

5. // 相加得

6. 0.01001100110011001100110011001100110011001100110011001110

0.01001100110011001100110011001100110011001100110011001110 转化为十进制就是 0.30000000000000004。验证完成！

JavaScript 的最大安全数是如何来的

根据双精度浮点数的构成，精度位数是 53bit。安全数的意思是在 -2^53~2^53 内的整数(不包括边界)与唯一的双精度浮点数互相对应。举个例子比较好理解：

1. Math.pow(2, 53) === Math.pow(2, 53) + 1 // true

Math.pow(2,53) 竟然与 Math.pow(2,53)+1 相等！这是因为 Math.pow(2, 53) + 1 已经超过了尾数的精度限制(53 bit)，在这个例子中 Math.pow(2,53) 和 Math.pow(2,53)+1 对应了同一个双精度浮点数。所以 Math.pow(2,53) 就不是安全数了。

最大的安全数为 Math.pow(2,53)-1，即 9007199254740991。

业务中碰到的精度问题以及解决方案

了解 JavaScript 精度问题对我们业务有什么帮助呢？举个业务场景：比如有个订单号后端 Java 同学定义的是 long 类型，但是当这个订单号转换成 JavaScript 的 Number 类型时候精度会丢失了，那没有以上知识铺垫那就理解不了精度为什么会丢失。

解决方案大致有以下几种：

1. 针对大数的整数可以考虑使用 bigint 类型(目前在 stage 3 阶段)。
2. 使用 bigNumber，它的思想是转化成 string 进行处理，这种方式对性能有一定影响。
3. 可以考虑使用 long.js，它的思想是将 long 类型的值转化成两个 32 位的双精度类型的值。

4. 针对小数可以考虑 JavaScript 浮点数陷阱及解法 里面提到的方案。

原文发布时间为：2018-11-08 本文作者：牧云云 

本文来自云栖社区合作伙伴“前端大学”，了解相关信息可以关注“前端大学”。