热门搜索:
您现在的位置是：首页 > 文章详情

JavaScript 算法与数据结构

日期：2018-06-07点击：538

本仓库包含了多种基于 JavaScript 的算法与数据结构。

每种算法和数据结构都有自己的 README 并提供相关说明以及进一步阅读和 YouTube 视频。

数据结构

数据结构是在计算机中组织和存储数据的一种特殊方式，它可以高效地访问和修改数据。更确切地说，数据结构是数据值的集合，它们之间的关系、函数或操作可以应用于数据。

算法

算法是如何解决一类问题的明确规范。 算法是一组精确定义操作序列的规则。

算法主题

算法范式

算法范式是基于类的设计的通用方法或方法的算法。 这是一个比算法概念更高的抽象，就像一个 算法是比计算机程序更高的抽象。

如何使用本仓库

安装依赖
 

npm install

执行测试 

npm test

按照名称执行测试 

npm test -- -t 'LinkedList'

Playground

你可以在./src/playground/playground.js文件中操作数据结构与算法，并在./src/playground/__test__/playground.test.js中编写测试。

然后，只需运行以下命令来测试你的 Playground 是否按无误:


npm test -- -t 'playground'

有用的信息

引用

▶ YouTube

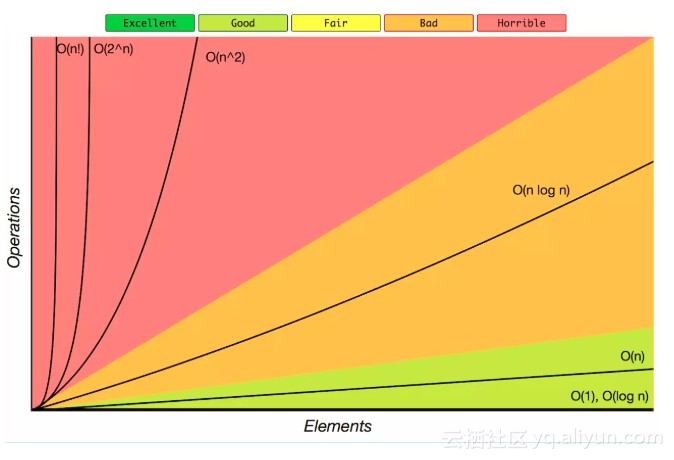
大O符号

大O符号中指定的算法的增长顺序。

d89b925016e12c9e33ffe513392baf294036e327

源: Big O Cheat Sheet.

以下是一些最常用的 大O标记法 列表以及它们与不同大小输入数据的性能比较。

大O标记法 计算10个元素 计算100个元素 计算1000个元素
O(1) 1 1 1
O(log N) 3 6 9
O(N) 10 100 1000
O(N log N) 30 600 9000
O(N^2) 100 10000 1000000
O(2^N) 1024 1.26e+29 1.07e+301
O(N!) 3628800 9.3e+157 4.02e+2567

数据结构操作的复杂性

数据结构 连接 查找 插入 删除
数组 1 n n n
栈 n n 1 1
队列 n n 1 1
链表 n n 1 1
哈希表 - n n n
二分查找树 n n n n
B树 log(n) log(n) log(n) log(n)
红黑树 log(n) log(n) log(n) log(n)
AVL树 log(n) log(n) log(n) log(n)

数组排序算法的复杂性

名称 最优 平均 最坏 内存 稳定
冒泡排序 n n^2 n^2 1 Yes
插入排序 n n^2 n^2 1 Yes
选择排序 n^2 n^2 n^2 1 No
堆排序 n log(n) n log(n) n log(n) 1 No
归并排序 n log(n) n log(n) n log(n) n Yes
快速排序 n log(n) n log(n) n^2 log(n) No
希尔排序 n log(n) 取决于差距序列 n (log(n))^2 1 No


原文发布时间为：2018年05月25日
原文作者：掘金
本文来源： 掘金 如需转载请联系原作者

原文链接：https://yq.aliyun.com/articles/610538
关注公众号

低调大师中文资讯倾力打造互联网数据资讯、行业资源、电子商务、移动互联网、网络营销平台。

持续更新报道IT业界、互联网、市场资讯、驱动更新,是最及时权威的产业资讯及硬件资讯报道平台。

转载内容版权归作者及来源网站所有，本站原创内容转载请注明来源。

相关文章

    文章评论

    共有0条评论来说两句吧...

    文章二维码

    扫描即可查看该文章

    点击排行

    推荐阅读

    最新文章