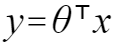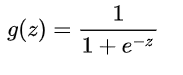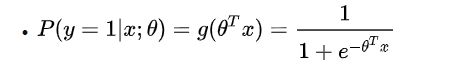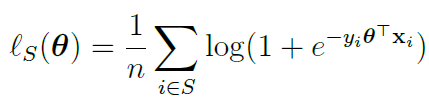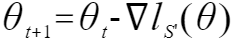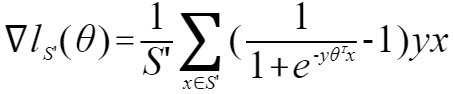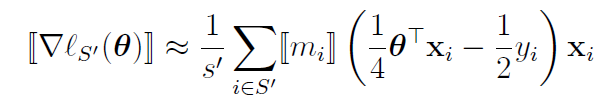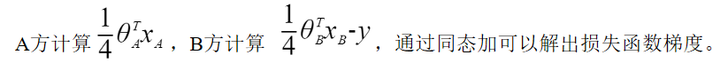摘要：主要介绍了华为云可信智能计算服务（TICS）采用的纵向联邦逻辑回归（LR）方案。

本文分享自华为云社区《纵向联邦学习场景下的逻辑回归（LR）》，作者： 汽水要加冰。

海量训练数据是人工智能技术在各个领域成功应用的重要条件。例如，计算机视觉和商务经融推荐系统中的 AI 算法都依靠大规模标记良好的数据才能获得较好的推理效果。然而在医疗、银行以及一些政务领域中，行业内对数据隐私的保护越来越强，造成可用数据严重匮乏的现状。针对上述问题，华为云可信智能计算服务（ TICS）专为打破银行、政企等行业的数据壁垒，实现数据安全共享，设计了多方联邦学习方案。

一、什么是逻辑回归？

回归是描述自变量和因变量之间相互依赖关系的统计分析方法。线性回归作为一种常见的回归方法，常用作线性模型（或线性关系）的拟合。

逻辑回归（logistic regression）虽然也称为回归，却不是一种模型拟合方法，而是一种简单的“二分类”算法。具有实现简单，算法高效等诸多优点。

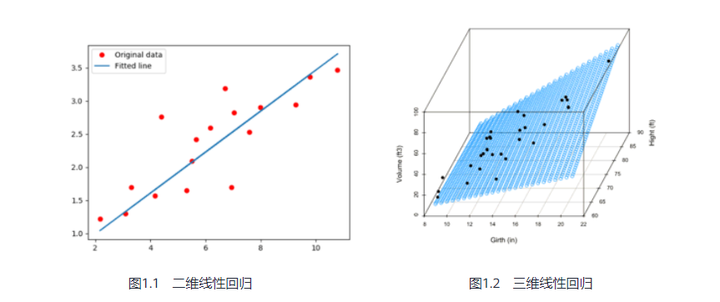
1.1 线性回归（linear regression）

图1.1、1.2分别表示二维和三维线性回归模型，图1.1的拟合直接（蓝线）可表示为 y=ax+b，所有数据点（红点）到直线的总欧式距离最短，欧式距离常用作计算目标损失函数，进而求解模型；类似的，图1.2的所有数据点到二维平面的总欧式距离最短。所以线性回归模型通常可以表示为：

其中θ表示模型系数。

1.2 逻辑回归（LR）

LR是一种简单的有监督机器学习算法，对输入x，逻辑回归模型可以给出 y<0 or y>0 的概率，进而推断出样本为正样本还是负样本。

LR引入sigmoid函数来推断样本为正样本的概率，输入样本 x 为正样本的概率可以表示为：P(y|x) = g(y)，其中 g() 为sigmoid函数，

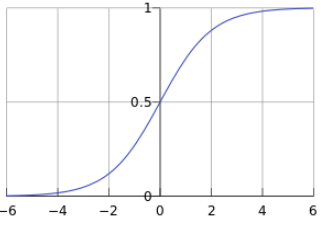
曲线图如图1.3所示，输出区间为0~1：

图1.3 sigmoid曲线

对于已知模型 θ 和样本 x，y=1的概率可以表示为：

所以sigmoid尤其适用于二分类问题，当 g(y) > 0.5 时，表示 P(y=1|x) > 0.5，将其判为正样本，对应 y>0 ；反之，当 g(y) < 0.5 时，表示 P(y=1|x) < 0.5，将其判为负样本，对应 y<0。

1.3 LR损失函数

LR采用对数损失函数，对于训练集x∈S，损失函数可以表示为（参考https://zhuanlan.zhihu.com/p/44591359）：

梯度下降算法是LR模型的经典解法之一，模型迭代更新的表达式如下：

其中

l()为目标损失函数，本质为平均对数损失函数。

• S'为批处理数据集(大小为batchsize)，通过批处理方式引入随机扰动，使得模型权重更加快速逼近最优值。
• α为学习率，直接影响模型的收敛速度，学习率过大会导致loss左右震荡无法达到极值点，学习率太小会导致loss收敛速度过慢，长时间找不到极值点。

二、纵向联邦学习场景下的LR

关于纵向联邦学习的介绍已经屡见不鲜，市面上也涌现出很多优秀的产品，比如FATE、华为可信智能计算TICS等。纵向联邦可以实现多用户在不暴露己方数据的前提下，共享数据和特征，训练出精度更高的模型，对于金融和政务等众多行业具有重要意义。

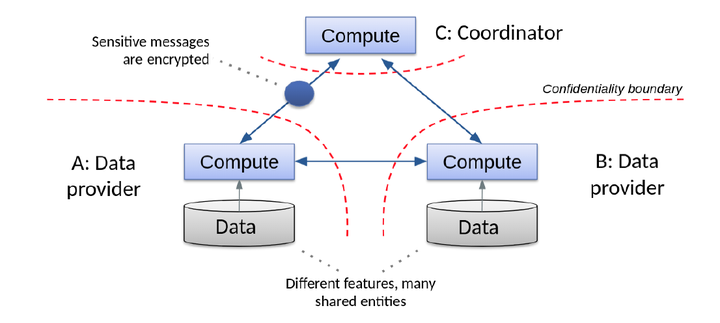
图2.1 纵向联邦LR

2.1 LR的纵向联邦实现

纵向联邦学习的参与方都是抱着共享数据、不暴露己方数据的目的加入到联邦中，所以任何敏感数据都必须经过加密才能出己方信任域（图2.1，参考https://arxiv.org/pdf/1711.10677.pdf），这就引入了同态加密算法。同态加密为密文计算提供了可行性，同时也一定程度上影响了机器学习算法的性能。常见的同态加密库包括seal、paillier等。

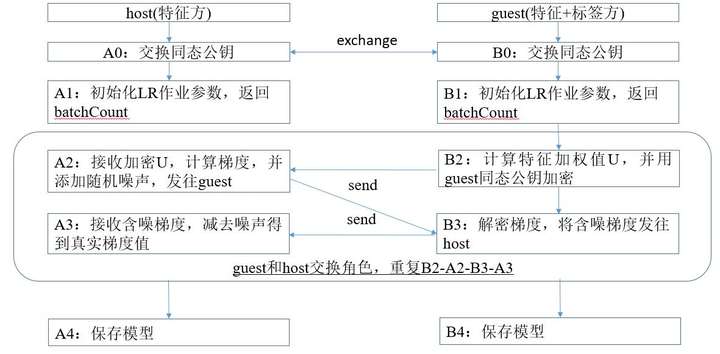
LR的纵向联邦流程如图2.2所示，host表示只有特征的一方，guest表示包含标签的一方。

图 2.2 纵向联邦LR算法实现流程

• 在训练开始之前，作业双方需要交换同态公钥。
• 每轮epoch（迭代）的batch（一轮batchsize的计算为一个batch）循环中，包含calEncryptedU-->calEncryptedGradient-->decryptGradient-->updateLrModel四步，guest和host都需要按此顺序执行一遍（ 流程图中只体现了guest作为发起方的执行流程）。
• A2步骤中梯度加随机噪声的目的是为了防止己方U泄露，造成安全问题。

由于同态加密计算只支持整数、浮点数的加法和乘法，所以将1.3中的模型迭代公式中的指数部分表示成泰勒表达式形式：

点击关注，第一时间了解华为云新鲜技术~