![97d7bac8b3b8f6cc1325aba9f1c8e8bc.png]()
撰文 | Will Zhang
本系列为CUDA进阶,通过具体的经典问题,讲述高性能编程的一些基本原则以及方法。建议读者先阅读NVIDIA官方的编程指南完成CUDA入门,基础比较少的同学也建议阅读本人之前写的GPU架构介绍。本文如有不对的地方欢迎指正。
首先我们不严谨地定义一下Reduction(归约), 给N个数值,求出其总和/最大值/最小值/均值这一类的操作,称为Reduction。如果是使用CPU,我们可以很简单的写一个循环遍历一遍即可完成。而在GPU上,我们如何并行利用几千个线程去做Reduction?
本文选取求总和为例子编写代码,相比内存访问,由于数值加法并不是很重的计算,所以这个问题中,主要注意的是如何利用好各级Memory的带宽。
1
Serial
我们先做一个Baseline,使用GPU上一个线程去遍历得到结果,如下:
__global__ void SerialKernel(const float* input, float* output, size_t n) {
float sum = 0.0f;
for (size_t i = 0; i < n; ++i) {
sum += input[i];
}
*output = sum;
}
void ReduceBySerial(const float* input, float* output, size_t n) {
SerialKernel<<<1, 1>>>(input, output, n);
}
其中n的值为4 * 1024 * 1024,也即输入的物理大小为4MByte。在作者的环境里,这段代码耗时为 100307us,我们后续的算法可以与这个作为对比。
2
TwoPass
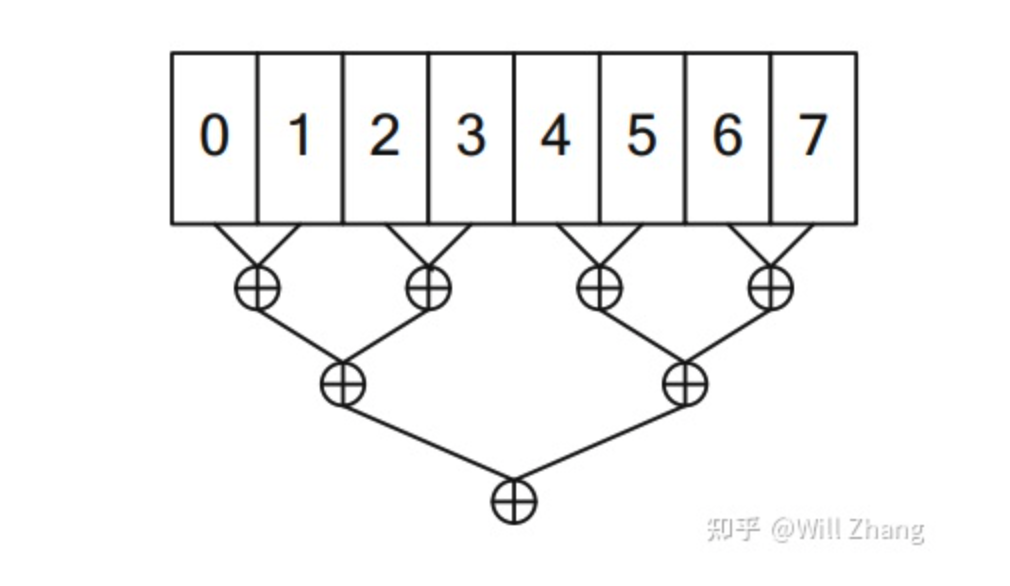
对于并发reduce这个问题,可以很容易想到一个朴素解法,以n=8为例,如下
![8b9f0a39f23d5c9d7164255b5e6a306c.png]()
我们把n均分为m个part,第一步启动m个block计算每个part的reduce结果,第二步启动一个单独的block汇总每个part的结果得到最终结果。其中每个block内部再把其负责的部分均分到每个线程,这样就可以得到一个朴素的代码如下
__global__ void TwoPassSimpleKernel(const float* input, float* part_sum,
size_t n) {
// n is divided to gridDim.x part
// this block process input[blk_begin:blk_end]
// store result to part_sum[blockIdx.x]
size_t blk_begin = n / gridDim.x * blockIdx.x;
size_t blk_end = n / gridDim.x * (blockIdx.x + 1);
// after follow step, this block process input[0:n], store result to part_sum
n = blk_end - blk_begin;
input += blk_begin;
part_sum += blockIdx.x;
// n is divided to blockDim.x part
// this thread process input[thr_begin:thr_end]
size_t thr_begin = n / blockDim.x * threadIdx.x;
size_t thr_end = n / blockDim.x * (threadIdx.x + 1);
float thr_sum = 0.0f;
for (size_t i = thr_begin; i < thr_end; ++i) {
thr_sum += input[i];
}
// store thr_sum to shared memory
extern __shared__ float shm[];
shm[threadIdx.x] = thr_sum;
__syncthreads();
// reduce shm to part_sum
if (threadIdx.x == 0) {
float sum = 0.0f;
for (size_t i = 0; i < blockDim.x; ++i) {
sum += shm[i];
}
*part_sum = sum;
}
}
void ReduceByTwoPass(const float* input, float* part_sum, float* sum,
size_t n) {
const int32_t thread_num_per_block = 1024; // tuned
const int32_t block_num = 1024; // tuned
// the first pass reduce input[0:n] to part[0:block_num]
// part_sum[i] stands for the result of i-th block
size_t shm_size = thread_num_per_block * sizeof(float); // float per thread
TwoPassSimpleKernel<<<block_num, thread_num_per_block, shm_size>>>(input,
part, n);
// the second pass reduce part[0:block_num] to output
TwoPassSimpleKernel<<<1, thread_num_per_block, shm_size>>>(part, output,
block_num);
}
这种分为两步的方法就称为Two-Pass,这个方法的时间为92us,相比之前的100307us确实快了许多。但是这个方法仍然比较朴素,没有利用好GPU特性。
首先读取Global Memory计算单线程的结果时,由于给单个线程划分了一块连续地址进行局部reduce,导致了同一个warp内的不同线程任意时刻读取的地址非连续。
打个比方,假设我们有9个数,使用3个线程去做局部reduce, 0号线程处理第0,1,2的数,1号线程处理第3,4,5的数,而第三个线程处理第6,7,8的数。于是有如下表:
![601566dc5cc24f6367d601c82a486a16.png]()
由于从Global Memory到SM的数据传输也是类似CPU Cache Line的方式,比如一次读取32*4=128字节,如果同一Warp内所有线程同时访问Global Memory连续的且对齐的128字节,那么这次读取就可以合并为一个Cache Line的读取。而在上面的情况下,由于每个线程读取的地址都不连续,意味着每次要触发多个CacheLine的读取。但是从Global Memory到SM的带宽并不是无限的,SM内以及L2能缓存下的数据也不是无限的,这意味着很可能会导致实际读了多次Global Memory, 同时带宽也被挤压导致延时上升.
需要注意,事实上GPU也支持32/64字节大小的CacheLine, 详情参考:
https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#device-memory-accesses
为了应对上文这种现象,我们应努力使得Warp内不同线程访问的地址连续,这会导致单个线程处理的地址不连续,在直觉上与CPU性能优化相反。仍然使用9数3线程的例子,列表如下:
![fa0526f6724272bdbd2b8553bc4d245c.png]()
我们可以写出优化后的kernel:
__global__ void TwoPassInterleavedKernel(const float* input, float* part_sum,
size_t n) {
int32_t gtid = blockIdx.x * blockDim.x + threadIdx.x; // global thread index
int32_t total_thread_num = gridDim.x * blockDim.x;
// reduce
// input[gtid + total_thread_num * 0]
// input[gtid + total_thread_num * 1]
// input[gtid + total_thread_num * 2]
// input[gtid + total_thread_num * ...]
float sum = 0.0f;
for (int32_t i = gtid; i < n; i += total_thread_num) {
sum += input[i];
}
// store sum to shared memory
extern __shared__ float shm[];
shm[threadIdx.x] = sum;
__syncthreads();
// reduce shm to part_sum
if (threadIdx.x == 0) {
float sum = 0.0f;
for (size_t i = 0; i < blockDim.x; ++i) {
sum += shm[i];
}
part_sum[blockIdx.x] = sum;
}
}
这个优化把时间从92us降低到了78us。
紧接着,更进一步,我们可以看到之前的代码,在把shared memory归约到最终值时采取了单线程遍历的简单方法,接下来我们优化这个步骤。
这里回顾一下shared memory的特性,其存在于SM上,意味着极快地访问延时与带宽,但其被分成32个Bank,与Warp的32线程对应。如果一个Warp内的32线程同时访问了32个不同的bank,也即没有任意两个线程访问同一bank,这时达到了最快的访存速度。否则,如果有两个线程同时访问了同一个bank,那么就会发生bank conflict,对这个bank的访存无法并发,形成顺序执行,也就意味着降低了访存速度。
如果访问了互斥的bank,那一定不会有bank conflict. 如果访问了相同的bank, 但是访问的是bank内的同一连续地址空间,也不会有bank conflict,这种情况下,如果都为读操作,则会广播给访问线程们,如果是写,则只有一个线程的写会成功,具体是哪个线程是未定义行为。
Shared Memory有4字节模式和8字节模式:
4字节模式:其中属于Bank 0的地址有[0, 4), [128, 132), [256, 260)...,而属于Bank 1的地址有[4, 8), [132, 136), [260, 264) ...,依次类推每个bank的地址。
8字节模式:其中属于Bank 0的地址有[0, 8), [256, 264), [512, 520)...,而属于Bank 1的地址有[8, 16), [264, 272), [520, 528) ...,依次类推每个bank的地址。
现在回到我们的问题,将存在于shared memory上的数据reduce,同时尽可能避免bank conflict,一般来说我们假设单个block的线程数是32的倍数,当然我们代码里实际也是如此,我们可以每次把数据的后半部分加到前半部分上,每次读写都没有bank conflict,代码如下
__global__ void TwoPassSharedOptimizedKernel(const float* input,
float* part_sum, size_t n) {
int32_t gtid = blockIdx.x * blockDim.x + threadIdx.x; // global thread index
int32_t total_thread_num = gridDim.x * blockDim.x;
// reduce
// input[gtid + total_thread_num * 0]
// input[gtid + total_thread_num * 1]
// input[gtid + total_thread_num * 2]
// input[gtid + total_thread_num * ...]
float sum = 0.0f;
for (int32_t i = gtid; i < n; i += total_thread_num) {
sum += input[i];
}
// store sum to shared memory
extern __shared__ float shm[];
shm[threadIdx.x] = sum;
__syncthreads();
// reduce shm to part_sum
for (int32_t active_thread_num = blockDim.x / 2; active_thread_num >= 1;
active_thread_num /= 2) {
if (threadIdx.x < active_thread_num) {
shm[threadIdx.x] += shm[threadIdx.x + active_thread_num];
}
__syncthreads();
}
if (threadIdx.x == 0) {
part_sum[blockIdx.x] = shm[0];
}
}
这一步优化从78us降低到了46us. 接下来更进一步的,如果活跃线程数少于等于32,也即只剩最后一个warp时,我们是不需要block级别的同步的,因为warp内必然同步(注意这里是无分支情况,不需要syncwarp,感谢评论区指正,之前的说法有误导嫌疑),改写为:
__global__ void TwoPassWarpSyncKernel(const float* input, float* part_sum,
size_t n) {
int32_t gtid = blockIdx.x * blockDim.x + threadIdx.x; // global thread index
int32_t total_thread_num = gridDim.x * blockDim.x;
// reduce
// input[gtid + total_thread_num * 0]
// input[gtid + total_thread_num * 1]
// input[gtid + total_thread_num * 2]
// input[gtid + total_thread_num * ...]
float sum = 0.0f;
for (int32_t i = gtid; i < n; i += total_thread_num) {
sum += input[i];
}
// store sum to shared memory
extern __shared__ float shm[];
shm[threadIdx.x] = sum;
__syncthreads();
// reduce shm
for (int32_t active_thread_num = blockDim.x / 2; active_thread_num > 32;
active_thread_num /= 2) {
if (threadIdx.x < active_thread_num) {
shm[threadIdx.x] += shm[threadIdx.x + active_thread_num];
}
__syncthreads();
}
// the final warp
if (threadIdx.x < 32) {
volatile float* vshm = shm;
if (blockDim.x >= 64) {
vshm[threadIdx.x] += vshm[threadIdx.x + 32];
}
vshm[threadIdx.x] += vshm[threadIdx.x + 16];
vshm[threadIdx.x] += vshm[threadIdx.x + 8];
vshm[threadIdx.x] += vshm[threadIdx.x + 4];
vshm[threadIdx.x] += vshm[threadIdx.x + 2];
vshm[threadIdx.x] += vshm[threadIdx.x + 1];
if (threadIdx.x == 0) {
part_sum[blockIdx.x] = vshm[0];
}
}
}
需要注意,使用warp隐式同步时使用shared memory需要配合volatile关键字。这个优化从46us降低到了40us.
更进一步的,我们可以把第二个for循环展开,同时我们要求在编译时就知道blockDim.x,而这可以通过template做到,这里我们仍然假设blockDim.x是32的倍数,此外限制其最大是1024,代码如下:
template <int32_t block_thread_num>
__global__ void TwoPassUnrollKernel(const float* input, float* part_sum,
size_t n) {
int32_t gtid = blockIdx.x * blockDim.x + threadIdx.x; // global thread index
int32_t total_thread_num = gridDim.x * blockDim.x;
// reduce
// input[gtid + total_thread_num * 0]
// input[gtid + total_thread_num * 1]
// input[gtid + total_thread_num * 2]
// input[gtid + total_thread_num * ...]
float sum = 0.0f;
for (int32_t i = gtid; i < n; i += total_thread_num) {
sum += input[i];
}
// store sum to shared memory
extern __shared__ float shm[];
shm[threadIdx.x] = sum;
__syncthreads();
// reduce shm
if (block_thread_num >= 1024) {
if (threadIdx.x < 512) {
shm[threadIdx.x] += shm[threadIdx.x + 512];
}
__syncthreads();
}
if (block_thread_num >= 512) {
if (threadIdx.x < 256) {
shm[threadIdx.x] += shm[threadIdx.x + 256];
}
__syncthreads();
}
if (block_thread_num >= 256) {
if (threadIdx.x < 128) {
shm[threadIdx.x] += shm[threadIdx.x + 128];
}
__syncthreads();
}
if (block_thread_num >= 128) {
if (threadIdx.x < 64) {
shm[threadIdx.x] += shm[threadIdx.x + 64];
}
__syncthreads();
}
// the final warp
if (threadIdx.x < 32) {
volatile float* vshm = shm;
if (blockDim.x >= 64) {
vshm[threadIdx.x] += vshm[threadIdx.x + 32];
}
vshm[threadIdx.x] += vshm[threadIdx.x + 16];
vshm[threadIdx.x] += vshm[threadIdx.x + 8];
vshm[threadIdx.x] += vshm[threadIdx.x + 4];
vshm[threadIdx.x] += vshm[threadIdx.x + 2];
vshm[threadIdx.x] += vshm[threadIdx.x + 1];
if (threadIdx.x == 0) {
part_sum[blockIdx.x] = vshm[0];
}
}
}
从40us降低到了38us。为了后文方便,我们把这个对shared memory reduce的过程提取一个函数称为ReduceSharedMemory,如下:
template <int32_t block_thread_num>
__device__ void ReduceSharedMemory(float* shm, float* result) {
if (block_thread_num >= 1024) {
if (threadIdx.x < 512) {
shm[threadIdx.x] += shm[threadIdx.x + 512];
}
__syncthreads();
}
if (block_thread_num >= 512) {
if (threadIdx.x < 256) {
shm[threadIdx.x] += shm[threadIdx.x + 256];
}
__syncthreads();
}
if (block_thread_num >= 256) {
if (threadIdx.x < 128) {
shm[threadIdx.x] += shm[threadIdx.x + 128];
}
__syncthreads();
}
if (block_thread_num >= 128) {
if (threadIdx.x < 64) {
shm[threadIdx.x] += shm[threadIdx.x + 64];
}
__syncthreads();
}
// the final warp
if (threadIdx.x < 32) {
volatile float* vshm = shm;
if (blockDim.x >= 64) {
vshm[threadIdx.x] += vshm[threadIdx.x + 32];
}
vshm[threadIdx.x] += vshm[threadIdx.x + 16];
vshm[threadIdx.x] += vshm[threadIdx.x + 8];
vshm[threadIdx.x] += vshm[threadIdx.x + 4];
vshm[threadIdx.x] += vshm[threadIdx.x + 2]; vshm[threadIdx.x] += vshm[threadIdx.x + 1];
if (threadIdx.x == 0) {
*result = vshm[0];
}
}
}
3
Single Pass
上一节中分为两次kernel,经过多次优化,降低到了38us。现在我们想办法,一次kernel完成我们的目标。
首先一个简单的办法,就是把之前的两步合并到一个kernel中,为了实现这个目标,我们需要一个计数器,每个block完成part sum计算时把计数器加1,当发现自己加完就是最后一个block,由这最后一个block去做part sum的归约,代码如下
__device__ int32_t done_block_count = 0;
template <int32_t block_thread_num>
__global__ void SinglePassMergedKernel(const float* input, float* part_sum,
float* output, size_t n) {
int32_t gtid = blockIdx.x * blockDim.x + threadIdx.x; // global thread index
int32_t total_thread_num = gridDim.x * blockDim.x;
// reduce
// input[gtid + total_thread_num * 0]
// input[gtid + total_thread_num * 1]
// input[gtid + total_thread_num * 2]
// input[gtid + total_thread_num * ...]
float sum = 0.0f;
for (int32_t i = gtid; i < n; i += total_thread_num) {
sum += input[i];
}
// store sum to shared memory
extern __shared__ float shm[];
shm[threadIdx.x] = sum;
__syncthreads();
// reduce shared memory to part_sum
ReduceSharedMemory<block_thread_num>(shm, part_sum + blockIdx.x);
// make sure when a block get is_last_block is true,
// all the other part_sums is ready
__threadfence();
// check if this block is the last
__shared__ bool is_last_block;
if (threadIdx.x == 0) {
is_last_block = atomicAdd(&done_block_count, 1) == gridDim.x - 1;
}
__syncthreads();
// reduce part_sum to output
if (is_last_block) {
sum = 0.0f;
for (int32_t i = threadIdx.x; i < gridDim.x; i += blockDim.x) {
sum += part_sum[i];
}
shm[threadIdx.x] = sum;
__syncthreads();
ReduceSharedMemory<block_thread_num>(shm, output);
done_block_count = 0;
}
}
void ReduceBySinglePass(const float* input, float* part, float* output,
size_t n) {
const int32_t thread_num_per_block = 1024;
const int32_t block_num = 1024;
size_t shm_size = thread_num_per_block * sizeof(float);
SinglePassMergedKernel<thread_num_per_block>
<<<block_num, thread_num_per_block, shm_size>>>(input, part, output, n);
}
这个版本的时间为39us,相比Two-Pass的时间略有增加。这些时间的对比结论并不是一定的,需要取决于数据的规模,以及gridDim和blockDim的选择,另外和GPU本身的型号也有关系,甚至和CPU的繁忙程度也有关系,所以数据对比作为参考即可。
另一个方法就是直接做Atomic:
__global__ void SinglePassAtomicKernel(const float* input, float* output,
size_t n) {
int32_t gtid = blockIdx.x * blockDim.x + threadIdx.x; // global thread index
int32_t total_thread_num = gridDim.x * blockDim.x;
// reduce
// input[gtid + total_thread_num * 0]
// input[gtid + total_thread_num * 1]
// input[gtid + total_thread_num * 2]
// input[gtid + total_thread_num * ...]
float sum = 0.0f;
for (int32_t i = gtid; i < n; i += total_thread_num) {
sum += input[i];
}
atomicAdd(output, sum);
}
这个方法的耗时是2553us,作为参考即可。
对于一个warp内的reduce,我们还可以使用warp级别的指令直接做这件事情,比如WarpReduce,由于这个指令不支持float,所以我们退而求其次,使用WarpShuffle也可以做到类似的事情,代码如下:
template <int32_t block_thread_num>
__device__ void ReduceSharedMemoryByShuffle(float* shm, float* result) {
if (block_thread_num >= 1024) {
if (threadIdx.x < 512) {
shm[threadIdx.x] += shm[threadIdx.x + 512];
}
__syncthreads();
}
if (block_thread_num >= 512) {
if (threadIdx.x < 256) {
shm[threadIdx.x] += shm[threadIdx.x + 256];
}
__syncthreads();
}
if (block_thread_num >= 256) {
if (threadIdx.x < 128) {
shm[threadIdx.x] += shm[threadIdx.x + 128];
}
__syncthreads();
}
if (block_thread_num >= 128) {
if (threadIdx.x < 64) {
shm[threadIdx.x] += shm[threadIdx.x + 64];
}
__syncthreads();
}
// the final warp
if (threadIdx.x < 32) {
volatile float* vshm = shm;
if (blockDim.x >= 64) {
vshm[threadIdx.x] += vshm[threadIdx.x + 32];
}
float val = vshm[threadIdx.x];
val += __shfl_xor_sync(0xffffffff, val, 16);
val += __shfl_xor_sync(0xffffffff, val, 8);
val += __shfl_xor_sync(0xffffffff, val, 4);
val += __shfl_xor_sync(0xffffffff, val, 2);
val += __shfl_xor_sync(0xffffffff, val, 1);
if (threadIdx.x == 0) {
*result = val;
}
}
}
使用这个指令的好处就是不需要shared memory,不过我们这个例子里体现不出优势来,耗时没有什么变化。
最后我们的最优耗时是38us,在本人机器下测试了cub的结果是49us,当然这也仅作为一个参考,具体的影响因素和具体的测试数据规模也有关,和GPU型号等也有关。不过通过这个例子,还是把很多知识点串起来了。
本文如有问题,欢迎指正,欢迎多交流(线上线下均可),共同学习共同进步,下一篇文章见。
本文获得授权后发布,原文链接:https://zhuanlan.zhihu.com/p/416959273
题图源自Pixabay
其他人都在看
点击“阅读原文”,欢迎下载体验OneFlow新一代开源深度学习框架
![390da956d7d4f5d103368307f79abd36.png]()