打开链接点亮社区Star，照亮技术的前进之路。 每一个点赞，都是社区技术大佬前进的动力 Github 地址： https://github.com/secretflow/secretflow

隐私信息检索(Private information retrieval PIR)也称为隐匿查询或匿踪查询，在医疗、股票、金融、社交等领域中都有大量应用场景。

近年来PIR技术研究逐渐丰富，行业对应用PIR实现隐私保护的呼声也随之高涨。

引言

[SealPIR][1]是微软开源的PIR实现，实现了2018年发表在IEEE S&P的论文[ACLS18][2]中的PIR方案。论文题目《PIR with Compressed Queries and Amortized Query Processing》已经包含了两个主要的贡献点：

• 对查询进行了压缩，通信量降低了274倍；

• 通过概率批量编码(probabilistic batch codes PBCs)可以同时执行多个查询，分摊查询处理的开销。

在近年的PIR协议研究中，特别是基于HE的PIR协议有很多进展，且大多数都是和SealPIR进行对比，因此理解SealPIR的原理也就有助于理解和跟踪he-based PIR近年来的发展。

本文将为小伙伴们介绍基于同态的隐私信息检索协议-SealPIR，欢迎大家在本文留言讨论。

1.PIR定义及分类

1.1 PIR定义

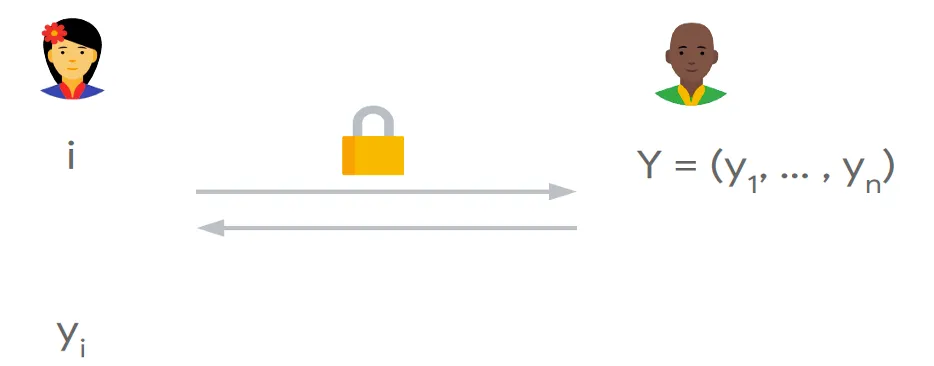
隐私信息检索(Private information retrieval PIR)是对信息检索(information retrieval IR)的一种扩展，最早在[CKGS95][3]中提出，用于保护用户查询信息，防止数据持有方得到用户的检索条件。

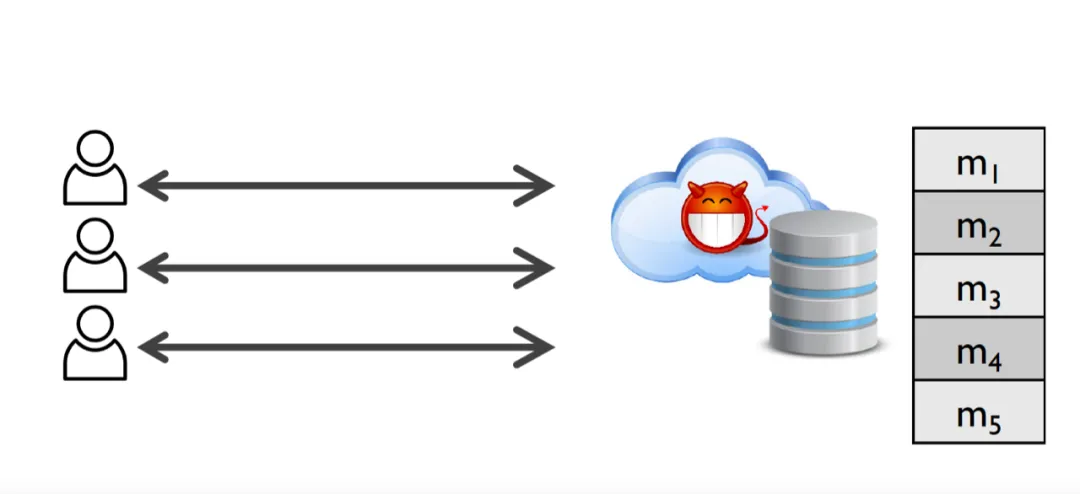
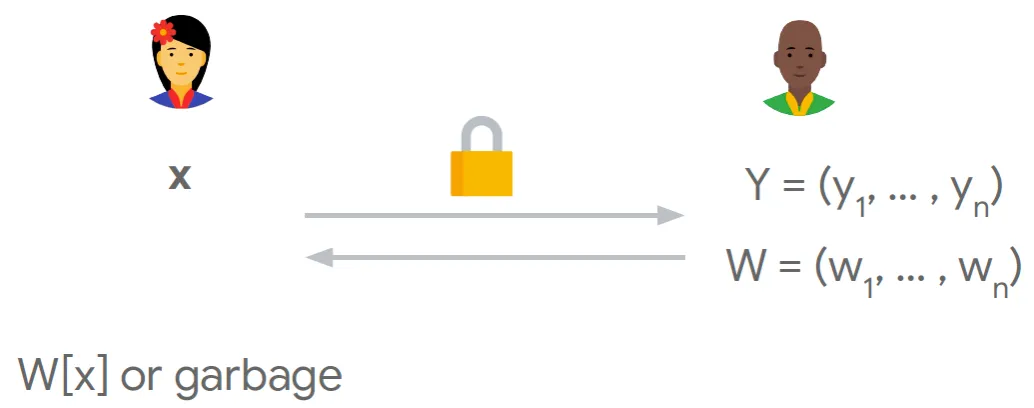
PIR协议目标可以定义为：Alice有共N行的数据库D，每一行的数据大小为L。Bob希望查询获得其中指定位置的某一行，但是不想告诉Alice自己查询的是哪一行。

隐私信息检索协议(PIR)需要满足正确性和安全性两方面的要求：

• 正确性：用户得到要查询的数据

• 安全性：服务端 无法知道 用户查询的是哪条数据

1.2 PIR分类

1.2.1 服务器数量分类

按照服务器数量分类可分为多服务器PIR和单服务器PIR。

• 多服务器PIR(MultiServer-PIR)

多服务器PIR一般基于信息论安全(Information-theoretic security)的密码技术，例如：基于函数密码分享(Function Secret Sharing)[BGI16][4]方案，也称为：IT-PIR。

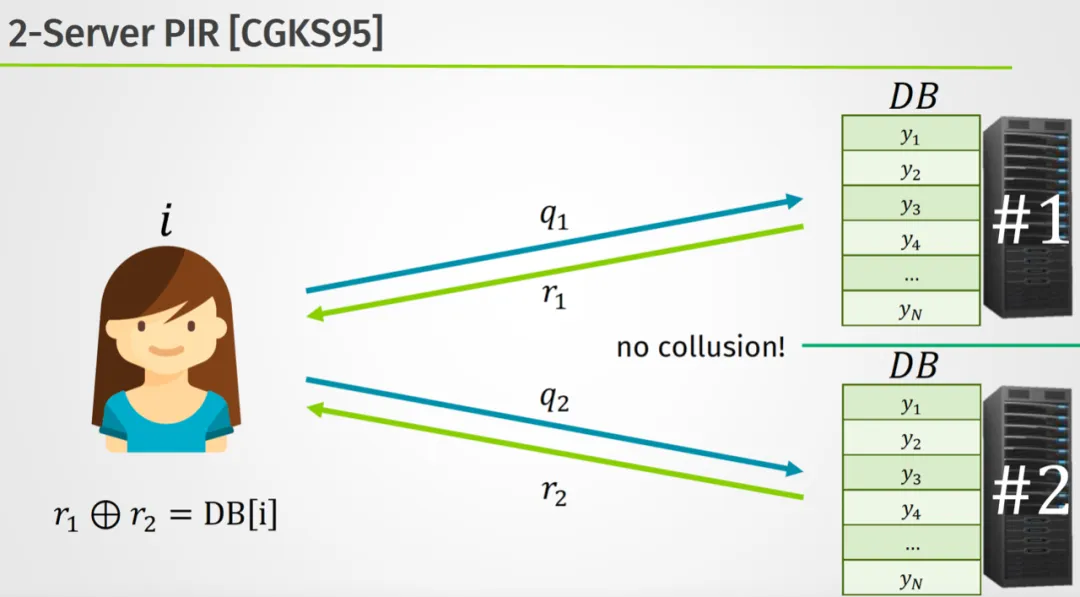
多服务器PIR协议大体流程如下：

1. 客户端生成查询条件的分量，发送给不同的服务器；

2. 服务器收到查询条件的分量后进行相应的计算，返回给客户端；

3. 客户端接收到所有服务器的响应后，将服务器查询响应看做秘密共享的分量进行合成，得到查询结果。

为了保护查询信息的安全，多服务器PIR方案中要求服务器之间是不能合谋的，增加了系统实现和部署的难度。

多服务器PIR方案中计算量相对较小，但通信量一般很大，大体规模是𝑛𝑜 (1)。

• 单服务器PIR(SingleServer-PIR)

单服务器PIR一般基于公钥密码方案，特别是同态性质的公钥密码方案，安全性基于计算复杂理论，也称为CPIR。

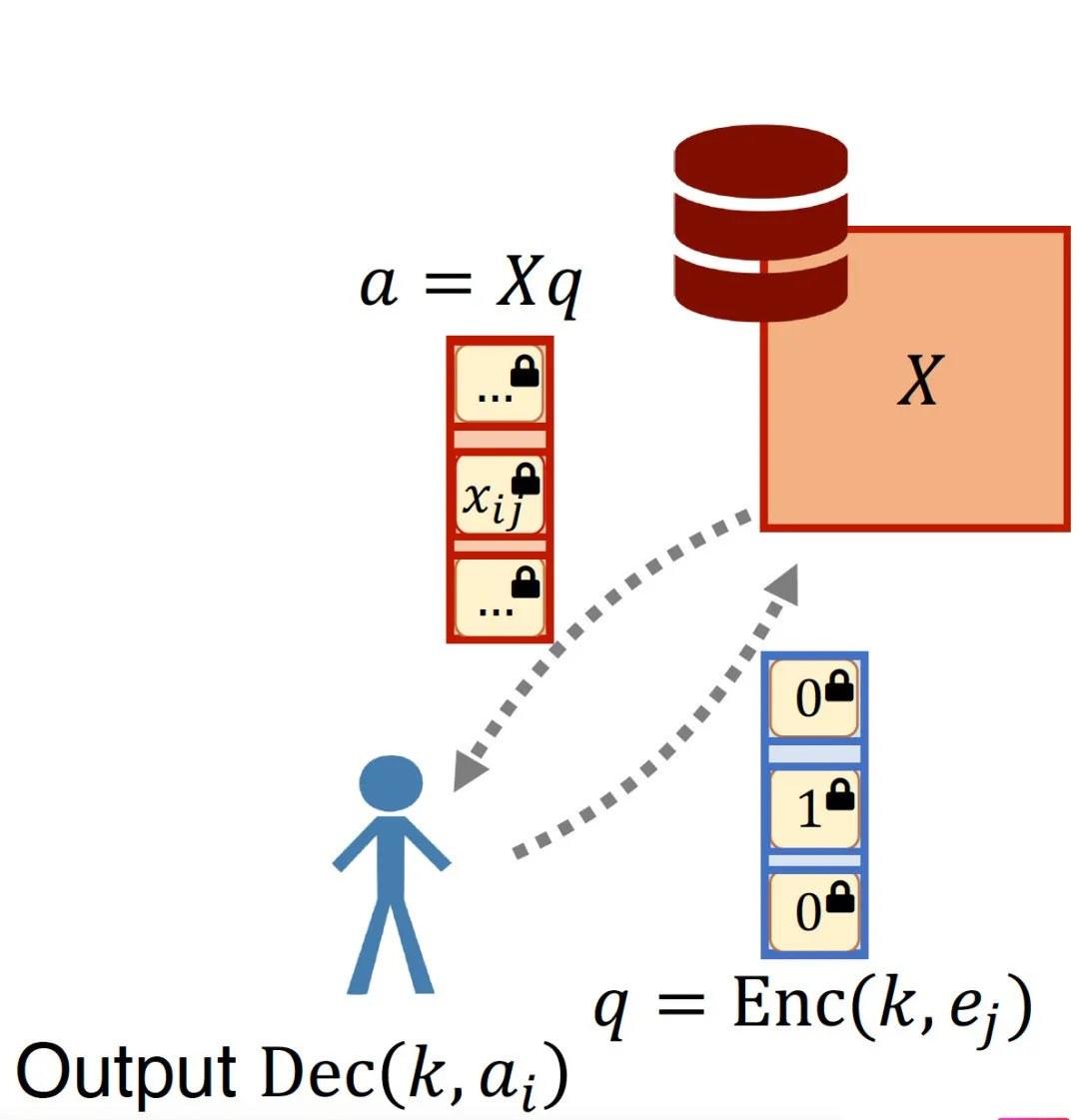
基于同态的单服务器PIR方案，大体流程如下：

1. 客户端生成加密的查询向量，发送给服务端;

2. 服务端接收到查询向量后，在本地执行同态运算，将结果返回给客户端；

3. 客户端收到响应后，解密得到查询结果。

单服务器PIR方案一般通信量较少，但计算量较大，且容易部署。

1.2.2 按照检索条件分类

• Index PIR/Dense PIR

服务端有n个元素的数据库𝐷={𝐷1,𝐷2,...,𝐷𝑛}，用户查询第𝑖个元素，通过执行PIR协议，用户得到𝐷𝑖，服务端不知道用户查询𝑖的信息。由于用户的查询条件在一个连续的集合[1...𝑛]，Index PIR也称为Dense-PIR。

• Keyword PIR/Sparse PIR

服务端的数据是(key,value)对构成的n个元素的数据库，用户选择自己要查询的key，通过执行PIR协议，用户得到key对应的value。这里查询条件key不能覆盖一个连续集合，例如：手机号或身份证，也称为Sparse PIR。

1.3 PIR性能指标

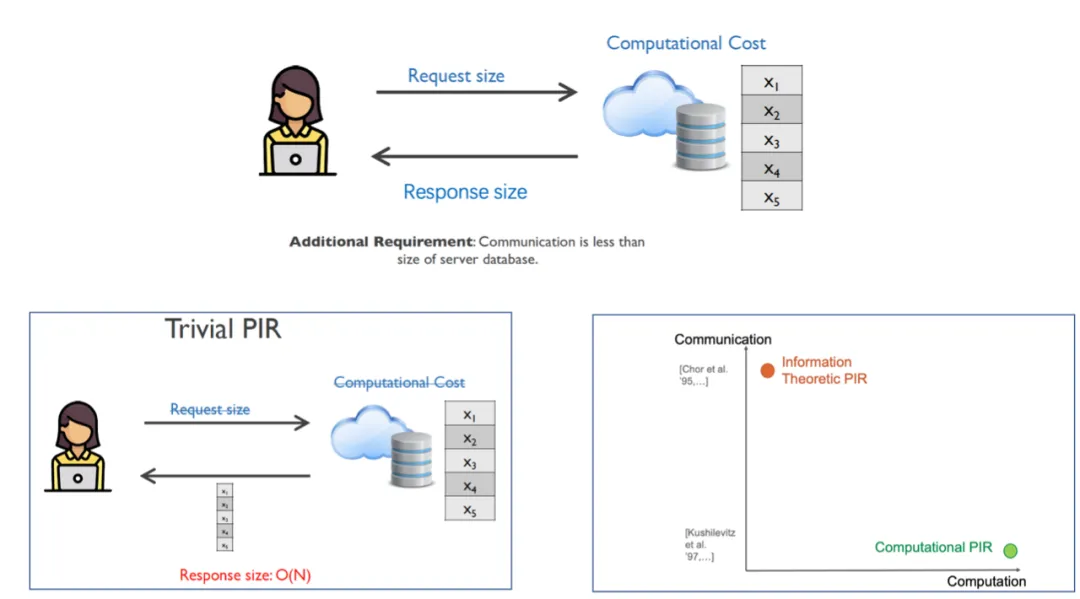
PIR的性能指标主要包括计算量和通信量。

• 计算量：计算量一般指的是服务端的计算量。

• 通信量：通信量可细分为查询请求的通信量和响应的通信量。

Trivial PIR中服务端没有计算量，将数据全部发给客户端，客户端在本地查询，通信量跟数据库中数据量n相关。

因此PIR的通信量要求小于数据库的容量。对比IT-PIR和CPIR的计算量和通信量可以看到，IT-PIR在计算量较少，但通信量较大；CPIR计算量较大，但通信量较小。

除了计算量和通信量两个指标外，有些论文里还引入了成本(monetary)作为指标，成本(monetary)指标实际上是对计算量和通信量平衡得到的指标，更适用于实际业务需求。

2.基础知识

目前Single-PIR最好的协议大多基于近似同态算法(Somewhat homomorphic encryption SHE)设计的，SealPIR中用到的是[BFV12][5]算法。

2.1 BFV方案

[BFV12]将[Brakerski12][6]中的同态算法从LWE迁移到RLWE，RLWE因为有特殊的结构比LWE性能更好，例如，RLWE选择特定参数时，乘法可以使用NTT(Number Theoretic Transform)。

BFV算法的参数包括：

• 多项式次数: 𝑁

• 明文模: 𝑡，素数

• 密文模: 𝑞，若干素数的乘积

明文空间是𝑅𝑡=𝑍𝑡\[𝑥\]/(𝑋𝑁+1)，即：𝑎0+𝑎1𝑥+...+𝑎𝑁-2𝑥𝑁-2+𝑎𝑁-1𝑥𝑁-1，𝑎𝑖∈𝑍𝑡

密文由两个多项式(𝑐0,𝑐1)构成，𝑐0,𝑐1∈𝑅𝑞=𝑍𝑞\[𝑥\]/(𝑋𝑁+1)。

密文扩张因子(Ciphertext expansion factor)，是指SHE加密后得到密文相对明文的增大的比例，对于BFV算法，密文扩张因子𝐹=2𝑙𝑜𝑔(𝑞)/𝑙𝑜𝑔(𝑡)。

对于128bit安全，同态加密标准中给出了推荐参数。考虑上面的密文扩展因子，明文模𝑡取相对较大时，能获得较小的密文扩张；但进行密文同态计算时，明文模𝑡太大时，会导致噪声增长太快，明文模𝑡也不能取得太大。

SealPIR中BFV参数中N和q选择举例如下表： | 多项式次数 | 明文模 | 密文模 | |------------|----------|--------------------| | 2048 | | 54bit | | 4096 | 38bit | 109bit 2*36+37 | | 8192 | 17bit | 218bit 243+344 |

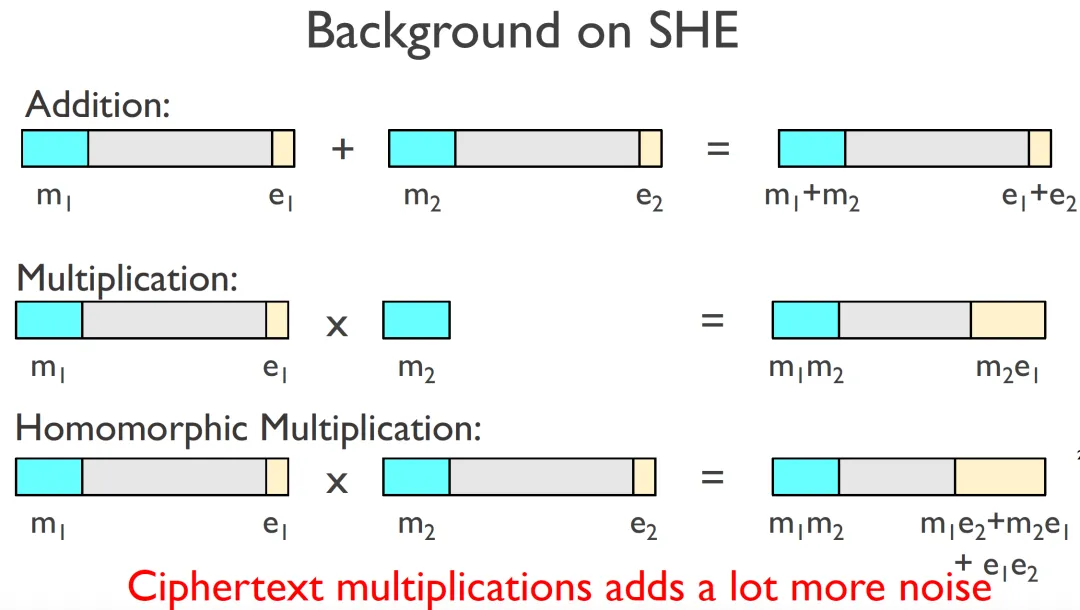
SealPIR中用到的同态运算：

• 密文加法：

明文𝑝1(𝑥)，𝑝2(𝑥)对应的密文是𝑐1和𝑐2，𝑐1+𝑐2是𝑝1(𝑥)+𝑝2(𝑥)的密文。

• 明文乘密文：

明文𝑝1(𝑥)对应的密文是𝑐1，𝑝2(𝑥)·𝑐1是𝑝1(𝑥)·𝑝2(𝑥)的密文。

• 替换：

明文𝑝(𝑥)对应的密文是𝑐，对于奇数𝑘，𝑆𝑢𝑏(𝑐,𝑘)是𝑝(𝑥𝑘)的密文。

例如，𝑝(𝑥)=7+𝑥2+2𝑥3，𝑆𝑢𝑏(𝑐,3)得到𝑝(𝑥3)=7+{𝑥3}2+2{𝑥3}3=7+𝑥6+2𝑥9的密文。

SHE的同态运算会引起噪声的增长，当噪声超过一定限制时，无法解密得到明文，所以要适当选择SHE算法的参数，及控制同态运算的噪声增长。

2.2 HE-based PIR

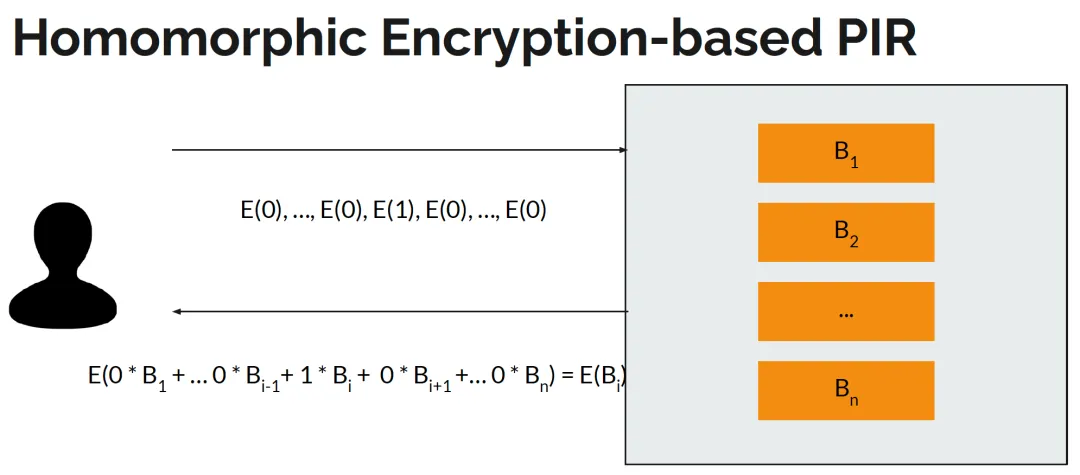
HE-based PIR基本原理如下图所示：

假设服务端数据量为𝑛，基本流程如下

1. 客户端生成BFV算法的私钥和公钥（𝑠𝑘,𝑝𝑘）;

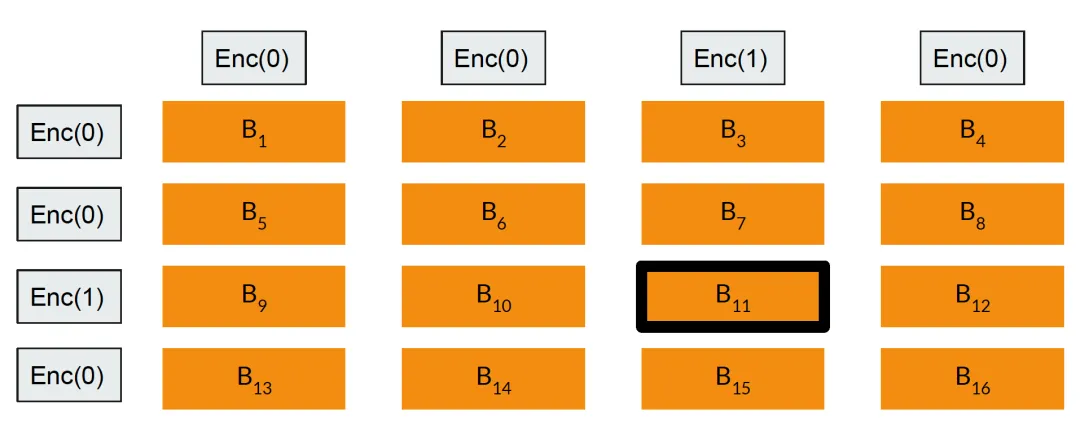
2. 客户端生成查询𝑛维0-1向量(0,...,0,1,0,...,0)，其中查询index 𝑖的位置位1，其它位置为0;

3. 客户端使用公钥加密查询向量的每个分量，得到(𝐸(0),...,𝐸(0),𝐸(1),𝐸(0),...,𝐸(0))，发送给服务端;

4. 服务端接收到密态查询向量后，和本地数据构成的𝑛维向量(𝐵1,𝐵2,...,𝐵𝑛)，进行点乘，得到𝐸(0·𝐵1+...+0·𝐵𝑖-1+𝐵𝑖+0·𝐵𝑖+1+...+0·𝐵𝑛)，发送给客户端;

5. 客户端对查询响应密文解密，得到待查询的数据𝐵𝑖。

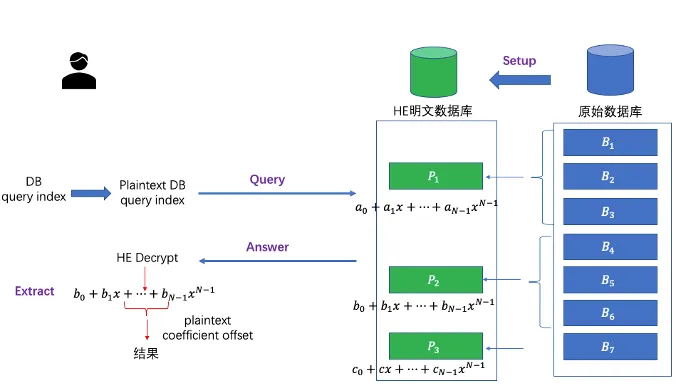
HE-based PIR协议可以抽象为四个子算法，即(Setup,Query,Answer,Extract)。

如下图所示：

• SETUP: 服务端 将数据库中的数据转换为HE明文

• QUERY: 客户端根据查询index，生成密态查询向量

• ANSWER: 服务端计算明文向量和密文向量的内积

• EXTRACT: 客户端使用私钥解密查询响应密文，得到查询数据

3.SealPIR协议

HE-based PIR基本原理中的协议，存在的问题是

• 查询请求的计算量和通信量都大，需要生成和发送𝑛个密文；

• 服务端每个数据表示为一个HE明文，需要计算n为向量的内积，容易导致噪声太大，无法解密

SealPIR论文给出了解决上面的问题的办法：

3.1 将多个数据pack到一个HE明文

查询的db\_index需要转换为plaintext\_index

假设数据库中数据长度为288字节(SealPIR论文中给出的长度)，BFV参数选择：多项式次数8192，明文模16bit，举例说明一下pack的效果：

• 数据库中每条数据，需要HE 明文多项式中个系数来表示𝐶𝑒𝑖𝑙(288*8/16)=144。

• HE 一个明文多项式可以包含𝐹𝑙𝑜𝑜𝑟(8192/144)=56调数据库数据。

• 对数据库的查询db_idx，需要转换为明文的查询plain_index=𝑑𝑏𝑖𝑑𝑥/56。

• 用户得到查询相应密文，通过私钥进行解密，得到HE明文，将HE明文对应的系数进行组合，得到真正查询的数据。

3.2 将查询向量压缩到一个密文

显著减少通信量，服务端增加一个额外的Expand操作得到查询密文向量。

查询向量(0,...,0,1,0,...,0)压缩到一个HE明文多项式为例，查询向量中的每个分量对应为HE 明文多项式中的系数。

𝑎0+𝑎1𝑥+...+𝑎𝑁-2𝑥𝑁-2+𝑎𝑁-1𝑥𝑁-1=𝑥𝑞𝑢𝑒𝑟𝑦_𝑖𝑛𝑑𝑒𝑥,其中：𝑎𝑖=0,𝑖≠𝑞𝑢𝑒𝑟𝑦_𝑖𝑛𝑑𝑒𝑥 ，𝑎𝑖=1,𝑖=𝑞𝑢𝑒𝑟𝑦_𝑖𝑛𝑑𝑒𝑥。

对查询明文进行加密，得到𝐸(𝑎0+𝑎1𝑥+...+𝑎𝑁-2𝑥𝑁-2+𝑎𝑁-1𝑥𝑁-1)=𝐸(𝑥𝑞𝑢𝑒𝑟𝑦_𝑖𝑛𝑑𝑒𝑥)。

服务端接收到查询密文后，执行Expand算法，得到查询密文向量：(𝐸(0),...,𝐸(0),𝐸(1),𝐸(0),...,𝐸(0))。

还是以上面packing的参数举例，每个HE明文可以pack 56个数据库数据，客户端查询时，将db\_index转换为plain\_index，即对HE明文数据库进行查询，最多可以查询8192个HE明文，转换成数据库数据，最多可以查询8192*56=458752条数据，不能满足实际业务中的需求。

为了满足实际将查询向量压缩到多个HE明文来表示查询向量，对于百万数据来讲，需要𝐶𝑒𝑖𝑙(1000000/8192)=123个HE明文，对应123个HE密文，才能表示百万数据的查询向量。

为了进一步压缩查询密文的数量，可以使用下面的多维表示方法。

Expand算法的详细描述和证明可以参考[ACLS18][2]论文中的内容。

3.3 将数据库一维向量转换为多维向量

二维查询时将数据库数据表示为√𝑛*√𝑛的矩阵，减少查询向量

以上面packing的参数举例，将数据库表示为2维数据时，通过两个查询密文可以查询的数据量是8192*8192*56≈37亿，已经能满足绝大多数的数据库查询任务。

数据库数据量为𝑛，通过packing后得到HE明文数量为𝑛′，𝐹是密文扩张因子，二维查询流程如下：

服务端：

• 将HE明文表示为√𝑛′*√𝑛′的矩阵𝑀，其中√𝑛′＜8192。

• 𝑉𝑐是密文查询列向量，𝐴𝑐=𝑀·𝑉𝑐，其中𝐴𝑐是√𝑛′ * 1的密文列向量。

• 将𝐴𝑐中每个密文拆分为𝐹份明文多项式，得到√𝑛′ * 𝐹矩阵𝐴𝑆𝑐。

• 𝑉𝑟是密文查询行向量，𝐴𝑆𝑇𝑐·𝑉𝑟，𝐹 * 1得到的密文向量。

客户端：

• 客户端收到𝐹个密文向量，使用私钥𝑠𝑘解密，将其组合成密文𝐸𝑛𝑐(𝑀[𝑟,𝑐])，对使用私钥𝑠𝑘解密𝐸𝑛𝑐(𝑀[𝑟,𝑐])得到真正的查询HE明文𝑀[𝑟,𝑐]，对HE明文𝑀[𝑟,𝑐]中对应的系数进行组合，得到真正查询的数据。

服务端为了避免进行密文乘以密文的同态运算，第3步中将密文拆解成𝐹个明文进行操作，最后服务端发给客户端的查询响应是𝐹个密文，在多项式次数8096时，𝐹≈26，因此，服务端发给客户端的查询响应消息太大，这也是SealPIR主要的问题，后续的文章，主要目标是减少查询响应消息，在后面的性能对比中可以看到。

3.4 通过一次进行多个查询降低整体性能开销

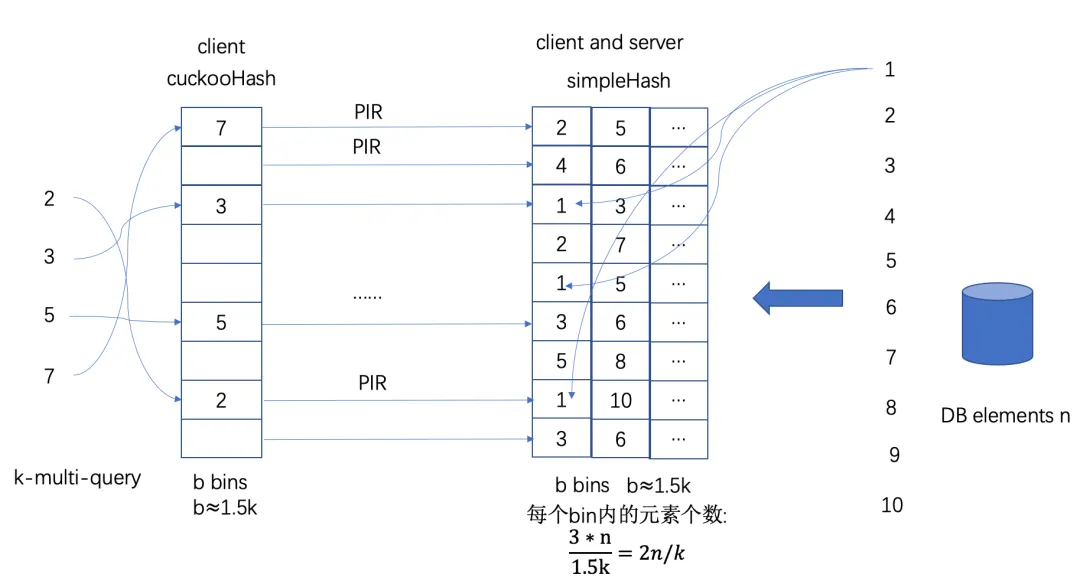
SealPIR论文中还给出了通过PBC(probabilistic batch code)将数据库中的内容分成若干batch，同时执行k个查询时，分别对不同的batch进行查询，降低整体的性能开销。论文给出了基于CuckooHash的PBC构造方案。

CuckooHash的hash数为3，bin数量为1.5𝑘，k为同时查询的数量。

服务端 预处理：

• 对DB中n个index，分别计算cuckooHash的3个Hash，得到3个bin_index,将(db_index, data)插入到3个bin_index中。

客户端 预处理：

• 对DB中n个index，分别计算cuckooHash的3个Hash，得到3个bin_index,将(db_index)插入到3个bin_index中。

• 将k个查询，通过cuckooHash，插入到𝑏=1.5𝑘个bin中，对空的bin进行随机填充。

• 对每个bin执行PIR，共计b个PIR，每个PIR的index，是客户端实际查询的data_idx，在bin中的索引。

从上图中可以看到，客户端生成的是CuckooHashTable和SimpleHashTable两张表，服务端生成的SimpleHashTable。

客户端和服务端SimpleHashTable的差别在于，服务端SimpleHashTable有实际待查询的数据，服务端SimpleHashTable只是模拟了服务端插入过程，bin中有db_index。

3.5 SealPIR的性能

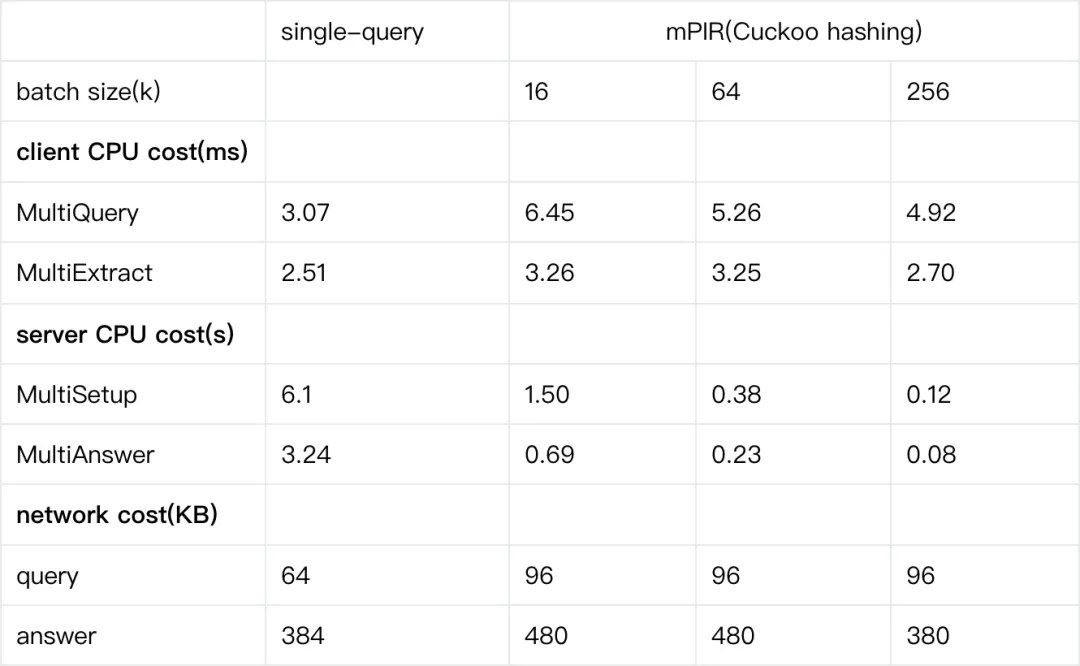
SealPIR论文Figure里给出single_query和multi-query的性能数据，多项式次数是2048，明文模式20bit，密文模式60bit，数据长度288字节，数据量220。

从上面可以看到，对于百万数据(220)单个查询的时间是3.3秒 左右，多个查询(256)性能可以降到0.1秒左右。

4.其它改进协议

这里介绍一下2021年的两篇PIR方面的文章：

• 发表在USENIX21年的[ALP+21][7]

• 发表在CCS21年的OnionPIR:[MCR21][8]

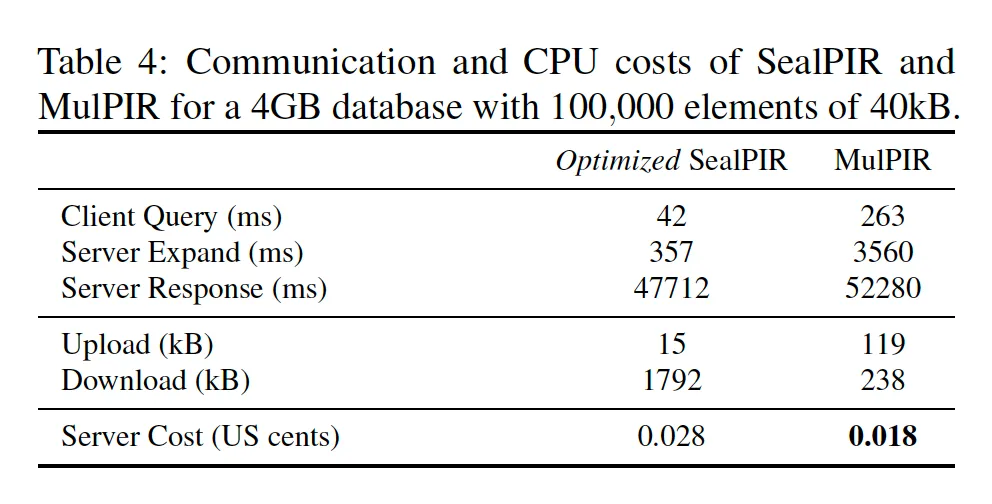
[ALP+21]题目是《Communication--Computation Trade-offs in PIR》是计算量和通信量平衡的PIR方案，该方案显著降低了查询响应的通信量，从成本(monetary)的角度看比SealPIR降低了35%。

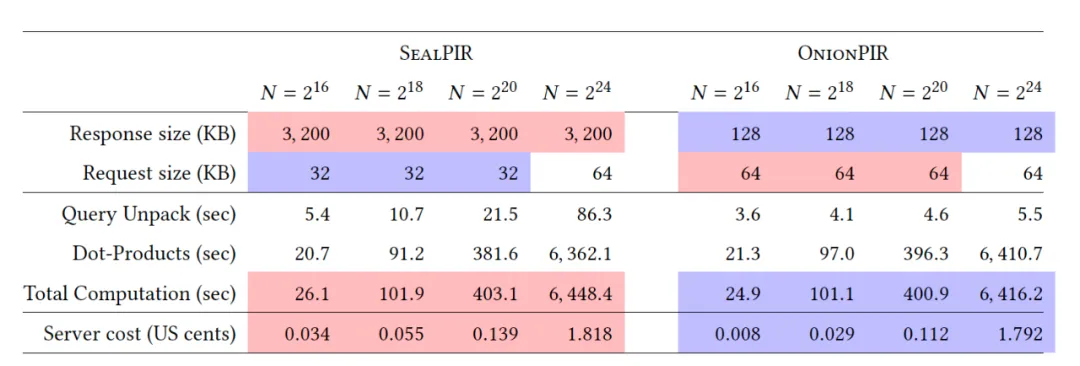
OnionPIR利用了somewhat homomorphic encryption(SHE)最新的进展，将两种lattice-based SHE 方案(BFV 和 RGSW)组合在一起，降低了查询响应的大小和计算量。还设计了基于状态(stateful)的PIR。

从上面的数据看到，虽然相应的改进协议对查询响应大小都有较大改进，但整体运行时间方面和SealPIR差别不大，由于引入了更复杂的算法，实现成本也会变得更高，综合来看SealPIR在实际应用中还是相对较好的选择。

💡 既然来都来了，花个1分钟点个 Star 再走吧！开源不易，每个人的点赞，都是社区技术大佬前进的动力~

打开链接即可点亮社区Star，照亮技术的前进之路。

Github 地址：https://github.com/secretflow/secretflow

参考文献

[1][SealPIR] SealPIR: A computational PIR library that achieves low communication

costs and high performance, 2020. https://github.com/microsoft/SealPIR.

[2][ACLS18] S. Angel, H. Chen, K. Laine and S. Setty,"PIR with Compressed Queries and Amortized Query Processing,"2018 IEEE Symposium on Security and Privacy (SP), 2018, pp. 962-979, doi: 10.1109/SP.2018.00062.

[3][CKGS95] B. Chor, O. Goldreich, E. Kushilevitz, and M. Sudan"Private information retrieval", in Proceedings of IEEE 36th Annual Foundations of Computer Science, pp. 41-50, Oct 1995.

[4][BGI16] Elette Boyle, Niv Gilboa, and Yuval Ishai.Function secret sharing: Improvements and extensions. In CCS, 2016.

[5][BFV12] Junfeng Fan and Frederik Vercauteren. 2012.Somewhat Practical Fully Homomorphic Encryption.IACR Cryptol. ePrint Arch. 2012 (2012), 144.

[6][Brakerski12] Zvika Brakerski.Fully Homomorphic Encryption without Modulus Switching from Clas-sical GapSVP. IACR Cryptology ePrint Archive, 2012:78, 2012.

[7][ALP+21] Asra Ali, Tancrède Lepoint, Sarvar Patel, Mariana Raykova, Phillipp Schoppmann, Karn Seth, and Kevin Yeo.

Communication-computation trade-o s in PIR. In USENIX Security, 2021.

[8][MCR21] M. Mughees, Hao Chen, Ling RenOnionPIR: Response Efficient Single-Server PIR, CCS'21.

[9][CGN98] Benny Chor, Niv Gilboa, and Moni Naor.

Private information retrieval by keywords.

IACR Cryptology ePrint Archive, 1998:3, 1998.

[10][CHLR18] Hao Chen, Zhicong Huang, Kim Laine, and Peter Rindal.

Labeled PSI from fully homomorphic encryption with malicious security.

In ACM Conference on Computer and Communications Security, pages 1223--1237. ACM, 2018.

本文由隐语社区统一发布，欢迎大家点 Star