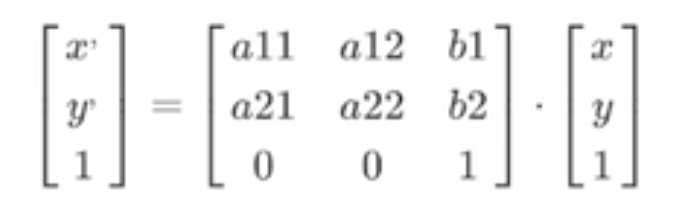import numpy as np
import math
from PIL import Image
import cv2
def affine_transform_numpy(image, transform_matrix):
"""
使用numpy实现仿射变换
Args:
image: 输入图像的numpy数组 (H, W, C)
transform_matrix: 2x3的仿射变换矩阵
Returns:
变换后的图像numpy数组
"""
h, w, channels = image.shape
# 创建输出图像
output = np.zeros_like(image)
# 计算变换矩阵的逆矩阵(用于反向映射)
# 将2x3矩阵扩展为完整的3x3矩阵,对应公式中的完整变换矩阵:
# [a11 a12 b1]
# [a21 a22 b2]
# [0 0 1 ] <- 齐次坐标的底行
full_matrix = np.vstack([transform_matrix, [0, 0, 1]])
print("完整的3x3变换矩阵:")
print(full_matrix)
try:
# 计算逆矩阵 - 用于反向映射
# 正向映射: [x', y'] = M * [x, y] (从原图到目标图)
# 反向映射: [x, y] = M^(-1) * [x', y'] (从目标图回到原图)
inv_matrix = np.linalg.inv(full_matrix)
print("逆变换矩阵:")
print(inv_matrix)
inv_transform = inv_matrix[:2, :] # 取前两行,得到2x3逆变换矩阵
print("用于反向映射的2x3矩阵:")
print(inv_transform)
except np.linalg.LinAlgError:
print("变换矩阵不可逆,返回原图像")
return image
# 创建目标图像的坐标网格 - 对应公式中的 [x', y', 1]
y_coords, x_coords = np.mgrid[0:h, 0:w]
# 将坐标转换为齐次坐标形式 [x', y', 1],每列是一个像素的坐标
coords = np.stack([x_coords.ravel(), y_coords.ravel(), np.ones(x_coords.size)])
print("目标图像坐标矩阵形状:", coords.shape)
print("前5个像素的齐次坐标:\n", coords[:, :5])
# 应用逆变换获取源图像坐标,跟原始公式不同,这里使用的是逆变换,@在python中是矩阵乘法
# [x, y, 1]^T = M^(-1) * [x', y', 1]^T
source_coords = inv_transform @ coords
source_x = source_coords[0].reshape(h, w)
source_y = source_coords[1].reshape(h, w)
# 双线性插值
for c in range(channels):
output[:, :, c] = bilinear_interpolation(image[:, :, c], source_x, source_y)
return output.astype(np.uint8)
def bilinear_interpolation(image, x_coords, y_coords):
"""
双线性插值
Args:
image: 单通道图像 (H, W)
x_coords: x坐标数组
y_coords: y坐标数组
Returns:
插值后的图像
"""
h, w = image.shape
output = np.zeros_like(x_coords)
# 找到有效的坐标范围
valid_mask = (x_coords >= 0) & (x_coords < w - 1) & (y_coords >= 0) & (y_coords < h - 1)
# 获取有效坐标
valid_x = x_coords[valid_mask]
valid_y = y_coords[valid_mask]
if len(valid_x) == 0:
return output
# 计算整数和小数部分
x0 = np.floor(valid_x).astype(int)
y0 = np.floor(valid_y).astype(int)
x1 = x0 + 1
y1 = y0 + 1
# 确保坐标在有效范围内
x1 = np.clip(x1, 0, w - 1)
y1 = np.clip(y1, 0, h - 1)
# 计算权重
dx = valid_x - x0
dy = valid_y - y0
# 双线性插值
# I(x,y) = I(x0,y0)(1-dx)(1-dy) + I(x1,y0)dx(1-dy) + I(x0,y1)(1-dx)dy + I(x1,y1)dxdy
interpolated = (image[y0, x0] * (1 - dx) * (1 - dy) +
image[y0, x1] * dx * (1 - dy) +
image[y1, x0] * (1 - dx) * dy +
image[y1, x1] * dx * dy)
output[valid_mask] = interpolated
return output
def create_rotation_matrix(theta):
"""
创建旋转变换矩阵
Args:
theta: 旋转角度(弧度)
Returns:
2x3的旋转矩阵
"""
cos_theta = math.cos(theta)
sin_theta = math.sin(theta)
# 对应公式中的2x3变换矩阵:
# [a11 a12 b1] [cos(θ) sin(θ) 0]
# [a21 a22 b2] = [-sin(θ) cos(θ) 0]
# 这是纯旋转矩阵,没有平移分量 (b1=0, b2=0)
rotation_matrix = np.array([
[cos_theta, sin_theta, 0], # [a11, a12, b1]
[-sin_theta, cos_theta, 0] # [a21, a22, b2]
], dtype=np.float32)
return rotation_matrix
def create_translation_matrix(tx, ty):
"""
创建平移变换矩阵
Args:
tx: x方向平移量
ty: y方向平移量
Returns:
2x3的平移矩阵
"""
translation_matrix = np.array([
[1, 0, tx],
[0, 1, ty]
], dtype=np.float32)
return translation_matrix
if __name__ == "__main__":
try:
# 使用PIL读取图像
pil_image = Image.open("/Users/admin/Documents/111.jpeg")
# 转换为numpy数组
img = np.array(pil_image)
if len(img.shape) == 3:
h, w, ch = img.shape
else:
# 如果是灰度图像,添加通道维度
img = np.expand_dims(img, axis=2)
h, w, ch = img.shape
print(f"图像尺寸: {h}x{w}x{ch}")
# 创建旋转变换矩阵(逆时针旋转15度)
theta = math.pi / 12 # 15度
rotation_matrix = create_rotation_matrix(theta)
# 可以组合多个变换,例如先旋转再平移
# translation_matrix = create_translation_matrix(100, 100)
# combined_matrix = translation_matrix @ np.vstack([rotation_matrix, [0, 0, 1]])
# transform_matrix = combined_matrix[:2, :]
# 旋转矩阵是2*2的,这里没有平移,故变换矩阵只有旋转矩阵
transform_matrix = rotation_matrix
print("变换矩阵:")
print(transform_matrix)
# 应用仿射变换
print("正在进行仿射变换...")
transformed_img = affine_transform_numpy(img, transform_matrix)
# 转换图像格式用于opencv显示 (RGB -> BGR)
if ch == 3:
img_bgr = cv2.cvtColor(img, cv2.COLOR_RGB2BGR)
transformed_img_bgr = cv2.cvtColor(transformed_img, cv2.COLOR_RGB2BGR)
else:
img_bgr = img
transformed_img_bgr = transformed_img
# 使用opencv显示图像
cv2.namedWindow('Original Image', cv2.WINDOW_NORMAL)
cv2.namedWindow('Transformed Image', cv2.WINDOW_NORMAL)
cv2.imshow('Original Image', img_bgr)
cv2.imshow('Transformed Image', transformed_img_bgr)
print("按任意键关闭窗口...")
cv2.waitKey(0)
cv2.destroyAllWindows()
# 保存变换后的图像
output_pil = Image.fromarray(transformed_img)
output_path = "/Users/admin/Documents/111_transformed.jpeg"
output_pil.save(output_path)
print(f"变换后的图像已保存到: {output_path}")
except FileNotFoundError:
print("错误: 找不到图像文件 /Users/admin/Documents/111.jpeg")
print("请确保图像文件存在,或修改文件路径")
except Exception as e:
print(f"处理图像时发生错误: {e}")
import numpy as np
import math
from PIL import Image
import cv2
def affine_transform_numpy(image, transform_matrix, fill_holes=True):
"""
使用numpy实现仿射变换(正向映射,优化版)
Args:
image: 输入图像的numpy数组 (H, W, C)
transform_matrix: 2x3的仿射变换矩阵
fill_holes: 是否填充空洞,默认True
Returns:
变换后的图像numpy数组
"""
h, w, channels = image.shape
# 创建输出图像
output = np.zeros_like(image)
# 正向映射:使用原始变换矩阵,完全按照数学公式
# [x', y'] = M * [x, y] (从原图到目标图)
print("正向映射变换矩阵 (2x3):")
print(transform_matrix)
# 优化坐标计算:直接创建坐标矩阵
print("创建坐标网格...")
y_indices, x_indices = np.mgrid[0:h, 0:w]
# 创建齐次坐标矩阵 (3, h*w)
coords = np.vstack([
x_indices.ravel(),
y_indices.ravel(),
np.ones(h * w, dtype=np.float32)
])
print("原图像坐标矩阵形状:", coords.shape)
print("前5个像素的齐次坐标:\n", coords[:, :5])
# 应用正向变换获取目标图像坐标,完全按照原始公式,@在python中是矩阵乘法
# [x', y']^T = M * [x, y, 1]^T
print("计算变换后坐标...")
target_coords = transform_matrix @ coords
target_x = target_coords[0].reshape(h, w)
target_y = target_coords[1].reshape(h, w)
print("变换后坐标范围:")
print(f"x': [{np.min(target_x):.2f}, {np.max(target_x):.2f}]")
print(f"y': [{np.min(target_y):.2f}, {np.max(target_y):.2f}]")
# 正向映射:使用向量化操作,大幅提升性能
print("使用向量化操作进行正向映射...")
# 向量化处理:找到所有有效的目标坐标
valid_mask = ((target_x >= 0) & (target_x < w) &
(target_y >= 0) & (target_y < h))
# 获取有效的坐标
valid_target_x = target_x[valid_mask]
valid_target_y = target_y[valid_mask]
# 四舍五入到整数坐标
target_x_int = np.round(valid_target_x).astype(int)
target_y_int = np.round(valid_target_y).astype(int)
# 确保坐标在边界内(向量化clip操作)
target_x_int = np.clip(target_x_int, 0, w - 1)
target_y_int = np.clip(target_y_int, 0, h - 1)
# 获取对应的原图像坐标
y_coords_flat = np.repeat(np.arange(h), w)
x_coords_flat = np.tile(np.arange(w), h)
valid_y_orig = y_coords_flat[valid_mask.ravel()]
valid_x_orig = x_coords_flat[valid_mask.ravel()]
# 向量化复制像素值
if channels == 1:
output[target_y_int, target_x_int] = image[valid_y_orig, valid_x_orig]
else:
for c in range(channels):
output[target_y_int, target_x_int, c] = image[valid_y_orig, valid_x_orig, c]
# 可选的后处理:填补空洞
if fill_holes:
output = fill_holes_simple(output)
print(f"变换完成!有效像素比例: {np.sum(output > 0) / output.size * 100:.2f}%")
return output.astype(np.uint8)
def fill_holes_simple(image):
"""
优化的空洞填充算法(向量化实现)
使用邻域平均值填充空洞(像素值为0的位置)
Args:
image: 包含空洞的图像
Returns:
填充后的图像
"""
if np.all(image != 0):
return image # 没有空洞,直接返回
print("正在填充空洞...")
output = image.copy()
h, w = image.shape[:2]
# 使用卷积进行快速邻域填充
from scipy import ndimage
if len(image.shape) == 3:
channels = image.shape[2]
for c in range(channels):
channel = image[:, :, c]
# 找到空洞位置
holes = (channel == 0)
if np.any(holes):
# 使用均值滤波填充
# 创建权重矩阵(忽略0值)
weights = (channel > 0).astype(float)
# 计算加权平均
kernel = np.ones((3, 3))
sum_values = ndimage.convolve(channel.astype(float), kernel, mode='constant')
sum_weights = ndimage.convolve(weights, kernel, mode='constant')
# 避免除以0
valid_weights = sum_weights > 0
filled_values = np.zeros_like(sum_values)
filled_values[valid_weights] = sum_values[valid_weights] / sum_weights[valid_weights]
# 只在空洞位置填充
output[holes, c] = filled_values[holes]
else:
# 灰度图像
holes = (image == 0)
if np.any(holes):
weights = (image > 0).astype(float)
kernel = np.ones((3, 3))
sum_values = ndimage.convolve(image.astype(float), kernel, mode='constant')
sum_weights = ndimage.convolve(weights, kernel, mode='constant')
valid_weights = sum_weights > 0
filled_values = np.zeros_like(sum_values)
filled_values[valid_weights] = sum_values[valid_weights] / sum_weights[valid_weights]
output[holes] = filled_values[holes]
return output
def bilinear_interpolation(image, x_coords, y_coords):
"""
双线性插值
Args:
image: 单通道图像 (H, W)
x_coords: x坐标数组
y_coords: y坐标数组
Returns:
插值后的图像
"""
h, w = image.shape
output = np.zeros_like(x_coords)
# 找到有效的坐标范围
valid_mask = (x_coords >= 0) & (x_coords < w - 1) & (y_coords >= 0) & (y_coords < h - 1)
# 获取有效坐标
valid_x = x_coords[valid_mask]
valid_y = y_coords[valid_mask]
if len(valid_x) == 0:
return output
# 计算整数和小数部分
x0 = np.floor(valid_x).astype(int)
y0 = np.floor(valid_y).astype(int)
x1 = x0 + 1
y1 = y0 + 1
# 确保坐标在有效范围内
x1 = np.clip(x1, 0, w - 1)
y1 = np.clip(y1, 0, h - 1)
# 计算权重
dx = valid_x - x0
dy = valid_y - y0
# 双线性插值
# I(x,y) = I(x0,y0)(1-dx)(1-dy) + I(x1,y0)dx(1-dy) + I(x0,y1)(1-dx)dy + I(x1,y1)dxdy
interpolated = (image[y0, x0] * (1 - dx) * (1 - dy) +
image[y0, x1] * dx * (1 - dy) +
image[y1, x0] * (1 - dx) * dy +
image[y1, x1] * dx * dy)
output[valid_mask] = interpolated
return output
def create_rotation_matrix(theta):
"""
创建旋转变换矩阵
Args:
theta: 旋转角度(弧度)
Returns:
2x3的旋转矩阵
"""
cos_theta = math.cos(theta)
sin_theta = math.sin(theta)
# 对应公式中的2x3变换矩阵:
# [a11 a12 b1] [cos(θ) sin(θ) 0]
# [a21 a22 b2] = [-sin(θ) cos(θ) 0]
# 这是纯旋转矩阵,没有平移分量 (b1=0, b2=0)
rotation_matrix = np.array([
[cos_theta, sin_theta, 0], # [a11, a12, b1]
[-sin_theta, cos_theta, 0] # [a21, a22, b2]
], dtype=np.float32)
return rotation_matrix
def create_translation_matrix(tx, ty):
"""
创建平移变换矩阵
Args:
tx: x方向平移量
ty: y方向平移量
Returns:
2x3的平移矩阵
"""
translation_matrix = np.array([
[1, 0, tx],
[0, 1, ty]
], dtype=np.float32)
return translation_matrix
if __name__ == "__main__":
try:
# 使用PIL读取图像
pil_image = Image.open("/Users/admin/Documents/111.jpeg")
# 转换为numpy数组
img = np.array(pil_image)
if len(img.shape) == 3:
h, w, ch = img.shape
else:
# 如果是灰度图像,添加通道维度
img = np.expand_dims(img, axis=2)
h, w, ch = img.shape
print(f"图像尺寸: {h}x{w}x{ch}")
# 创建旋转变换矩阵(逆时针旋转15度)
theta = math.pi / 12 # 15度
rotation_matrix = create_rotation_matrix(theta)
# 可以组合多个变换,例如先旋转再平移
# translation_matrix = create_translation_matrix(100, 100)
# combined_matrix = translation_matrix @ np.vstack([rotation_matrix, [0, 0, 1]])
# transform_matrix = combined_matrix[:2, :]
# 正向映射:直接使用2x3变换矩阵,按照数学公式 [x', y'] = M * [x, y, 1]
transform_matrix = rotation_matrix
print("变换矩阵:")
print(transform_matrix)
# 应用仿射变换(正向映射)
print("正在进行仿射变换(正向映射)...")
import time
start_time = time.time()
# 可以选择是否填充空洞(填充空洞会增加处理时间)
fill_holes_option = True # 改为False可以跳过空洞填充,提升性能
transformed_img = affine_transform_numpy(img, transform_matrix, fill_holes=fill_holes_option)
end_time = time.time()
print(f"变换耗时: {end_time - start_time:.3f} 秒")
# 转换图像格式用于opencv显示 (RGB -> BGR)
if ch == 3:
img_bgr = cv2.cvtColor(img, cv2.COLOR_RGB2BGR)
transformed_img_bgr = cv2.cvtColor(transformed_img, cv2.COLOR_RGB2BGR)
else:
img_bgr = img
transformed_img_bgr = transformed_img
# 使用opencv显示图像
cv2.namedWindow('Original Image', cv2.WINDOW_NORMAL)
cv2.namedWindow('Transformed Image', cv2.WINDOW_NORMAL)
cv2.imshow('Original Image', img_bgr)
cv2.imshow('Transformed Image', transformed_img_bgr)
print("按任意键关闭窗口...")
cv2.waitKey(0)
cv2.destroyAllWindows()
# 保存变换后的图像
output_pil = Image.fromarray(transformed_img)
output_path = "/Users/admin/Documents/111_transformed.jpeg"
output_pil.save(output_path)
print(f"变换后的图像已保存到: {output_path}")
except FileNotFoundError:
print("错误: 找不到图像文件 /Users/admin/Documents/111.jpeg")
print("请确保图像文件存在,或修改文件路径")
except Exception as e:
print(f"处理图像时发生错误: {e}")
透视变换
仿射变换是在二维空间中的旋转、平移和缩放,透视变换是在三维空间中的视角变化。相对于仿射,透视变换能保持"直线性",原图像中的直线,经透视变换后仍为直线。
透视变换(Perspective Transformation)是一种非线性几何变换,模拟了三维空间中的物体投影到二维平面上的过程,就像人眼看物体或相机拍照的原理。
如果说仿射变换是对三维空间中某个平面的一些二维变化,透视变换就是对这个平面进行变换,并且利用视觉原理对图像进行一定处理(近大、远小)。
![]()
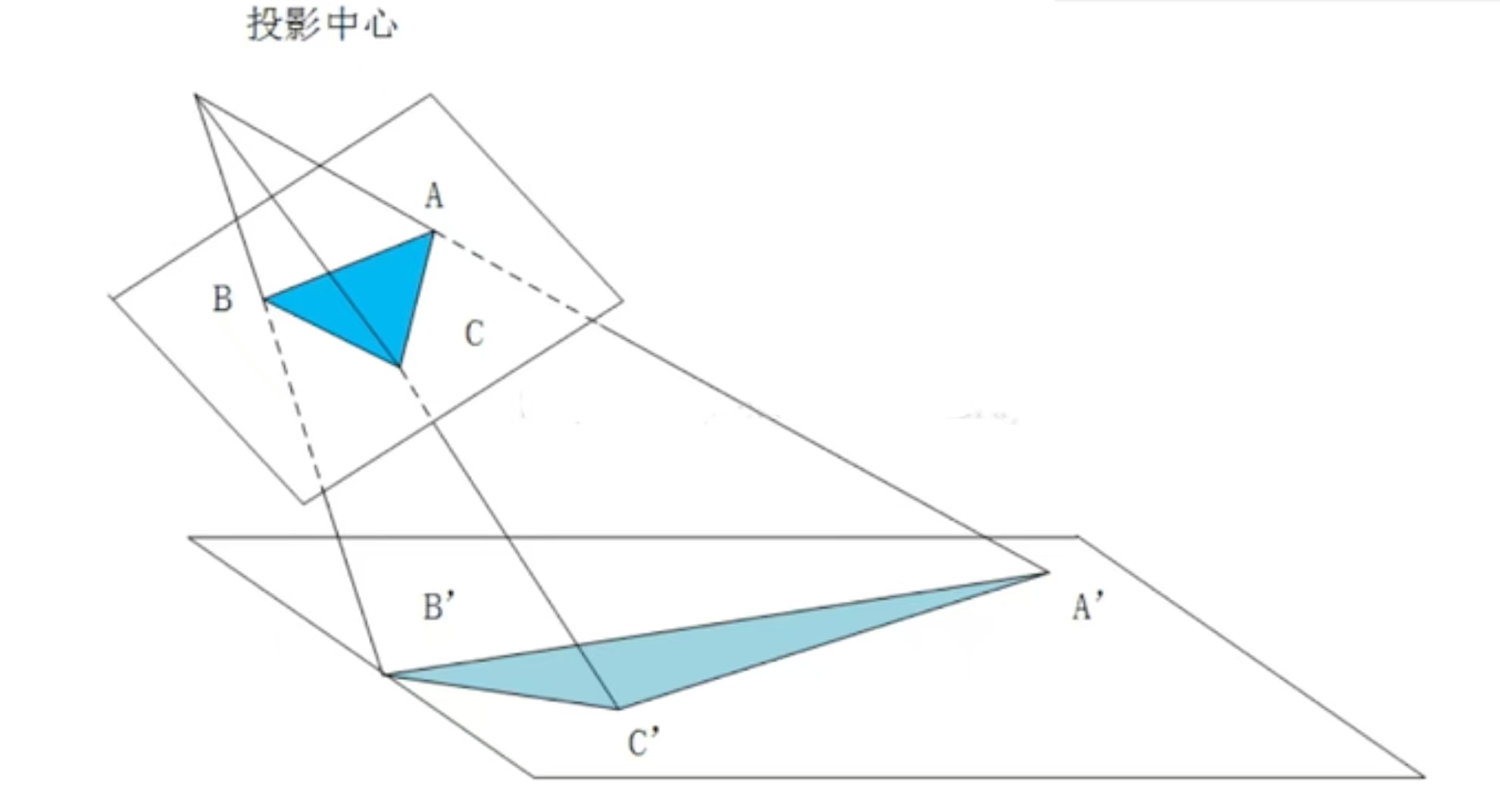
- 图中顶部标注的"投影中心"是透视变换的核心点
- 就像人的眼睛位置或相机镜头的光心
- 所有的投影线都从这个点发出
- 深蓝色三角形ABC是原始图形
- 位于较近的投影平面上
- 各个顶点坐标为A、B、C
- 浅蓝色三角形A'B'C'是透视变换的结果
- 位于较远的投影平面上
- 各个顶点坐标为A'、B'、C'
透视变换的详细步骤
- 第一步:建立投影射线,从投影中心分别向原图形的每个顶点画射线:
- 投影中心 → A点:形成射线PA
- 投影中心 → B点:形成射线PB
- 投影中心 → C点:形成射线PC
- 第二步:确定目标投影平面,设定一个新的投影平面(图中下方的平面),这个平面通常:
- 平行于原平面,但距离投影中心更远
- 或者以某个角度倾斜
- 第三步:计算交点坐标,每条投影射线与目标平面的交点就是变换后的坐标:
- 射线PA与目标平面交于A'
- 射线PB与目标平面交于B'
- 射线PC与目标平面交于C'
- 连接新的顶点A'、B'、C',形成变换后的三角形
- 注意:形状发生了显著变化,不再是相似变换
透视变换的数学特征
- 直线仍保持直线(除了通过投影中心的直线)
- 角度不保持不变**
- 长度比例不保持不变**
- 面积比例不保持不变**
- [x'] [h11 h12 h13] [x]
- [y'] = [h21 h22 h23] [y]
- [w'] [h31 h32 h33] [w]
- 最终坐标:x_final = x'/w', y_final = y'/w'
- 从图中可以看出,离投影中心近的物体(ABC)看起来较大
- 离投影中心远的物体(A'B'C')看起来较小
- 这正是透视效果的本质
齐次坐标系与笛卡尔坐标系
我们说透视变换是非线性变换,但是从上面的公式来看,在齐次坐标系中它满足线性变换的基本格式,但最终我们需要转换回笛卡尔坐标。
齐次坐标系
我们知道线性变换x'=Ax无法改变原点,即无法发生位移。但仿射变换x'=Ax+b可以,为什么我们要将这一加法操作转变为直接的矩阵乘法操作呢?
![]()
我们将平移值\([b_1 b_2]^T\),即向量b放在矩阵的右上角达到了相同的结果
- \(x'=a_{11}x+a_{12}y+b_1\)
- \(y'=a_{21}x+a_{22}y+b_2\)
- 1=1
这里的1=1很重要,我们知道对于平面上的运算,二维就够了,可为什么要用到三维坐标呢?这里就需要引入齐次坐标的概念。
齐次坐标是一种用n+1维来表示n维点的方法。简单来说,就是用额外的维度来表示点的"权重"或"深度"。它的好处就是可以使用矩阵乘法。
对于计算机来说,如果只使用二维的加法运算,对于一个图形有大量的点,计算耗时耗力,而矩阵乘法对于GPU来说,只需要一步完成。
而齐次坐标由\([x\ y\ 1]^T\)变成\([x\ y\ 0]^T\)时,其实就是没有平移的线性变换,原点不变。但其实齐次坐标为0时又表示平面内的无穷远点,我们知道只有二维坐标\([x\ y]^T\)时,无论x,y取何值,都无法表达∞这个概念,而\([x\ y\ 0]^T\)的齐次坐标则表达为无穷远点,它只表达方向。那既不是1又不是0时会怎样呢?如\([x\ y\ w]^T\),可以看作是3D空间中从原点出发的射线。在这种情况下,规则是要将恢复的的向量的每个分量除以齐次坐标w,以使齐次值回到1
\([\frac {x}{w}\ \frac {y}{w}\ 1]^T\)
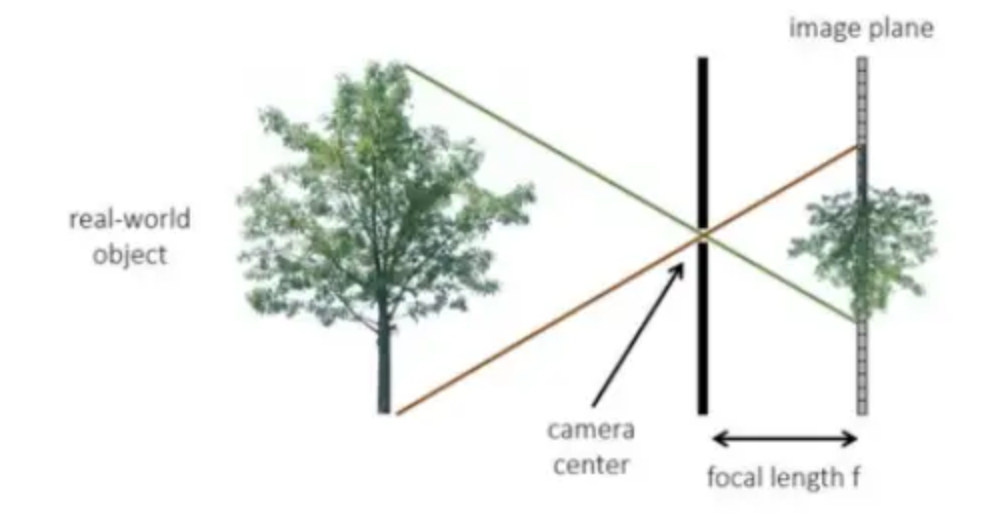
那么这里的\(\frac {x}{w}\)和\(\frac {y}{w}\)就是笛卡尔坐标系中的坐标。齐次坐标w表示一个归一化的深度值,该值越大,投影后的物体越小;该值越小,投影后的物体越大。这里我们用透镜成像来理解就会更简单。
![]()
上图中,投影中心就是透镜的中心点,它到真实物体树的垂直距离为Z,它到后方投影平面的距离为焦距f,则\(w=\frac {Z}{f}\),在f固定不变的情况下,Z越大,w越大,在成像平面中,树的像就越小(这里需要注意的是树不是等比例放大的,它在任何位置都是同样大小的,越远的树的上下两端与原点的夹角就会越小,成像也会越小)。固定Z不变,f越小,w越大,在成像平面中,树也会越来越小。
笛卡尔坐标系
笛卡尔坐标系简单理解就是我们最常用的二维平面直角坐标系,也是仿射变换的基础。齐次坐标系就是一个三维空间坐标系,但是\([x\ y\ w]^T\)中的w并不表示一个距离坐标,它仅仅只是一个数学参数,代表权重;x,y是成像平面中的二维坐标。
透视变换矩阵
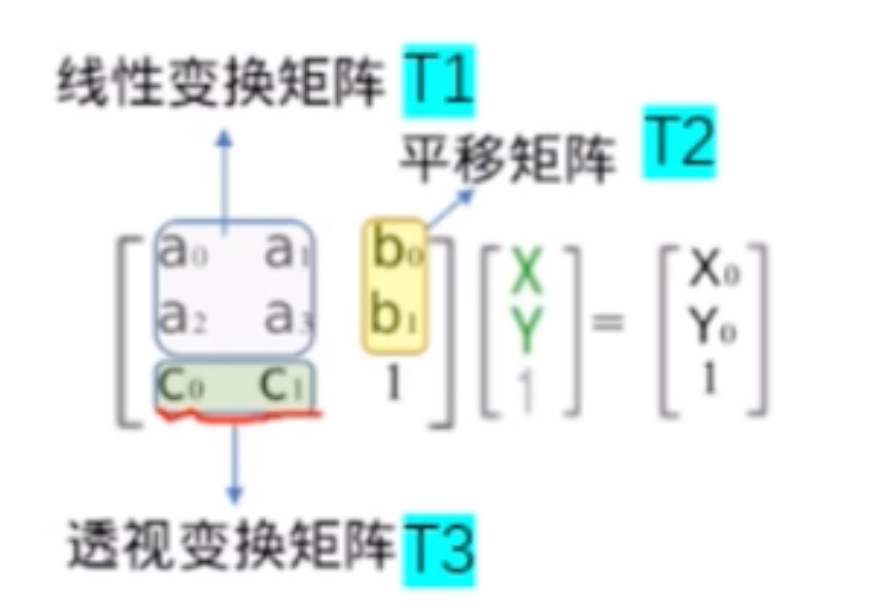
![]()
在上图中,透视变换矩阵指的是\(c_0,c_1\)所组成的T3,相比于二维平面的齐次坐标(旋转、平移)
![]()
这里的\(c_0,c_1\)如果不为0,则它不再是二维平面的齐次坐标,它是用来控制齐次值w的,它们满足以下的关系
\(w=c_0x+c_1y+1\)
最终的笛卡尔坐标就为
- \(x''=\frac {x'}{w}=\frac {a_{11}x+a_{12}y+b_1}{c_0x+c_1y+1}\)
- \(y''=\frac {y'}{w}=\frac {a_{21}x+a_{22}y+b_2}{c_0x+c_1y+1}\)
这就是归一化后的透视变换方程
注:这里的x''、y''是透视变换后的笛卡尔坐标,x'、y'是仿射变换后的笛卡尔坐标
透视变换代码样例
实例可以参考OpenCV计算机视觉整理 中的透视变换。这里我们将不使用opencv内置方法,而使用numpy来重写
import numpy as np
import cv2
from PIL import Image
import time
def perspective_transform_numpy(image, src_points, dst_points):
"""
使用numpy实现透视变换
"""
h, w, channels = image.shape
# 计算透视变换矩阵
print("计算透视变换矩阵...")
M = compute_perspective_transform(src_points, dst_points)
print("透视变换矩阵:")
print(M)
# 获取目标图像尺寸
dst_h, dst_w = get_dst_size(dst_points)
print(f"目标图像尺寸: {dst_w} x {dst_h}")
# 创建输出图像
output = np.zeros((dst_h, dst_w, channels), dtype=np.uint8)
# 计算逆变换矩阵(用于反向映射)
print("计算逆变换矩阵...")
inv_M = np.linalg.inv(M)
# 创建目标图像的坐标网格
print("创建目标图像坐标网格...")
y_coords, x_coords = np.mgrid[0:dst_h, 0:dst_w]
# 转换为齐次坐标 (3, h*w)
coords = np.vstack([
x_coords.ravel(),
y_coords.ravel(),
np.ones(dst_h * dst_w, dtype=np.float32)
])
# 应用逆变换获取源图像坐标
print("应用逆变换...")
source_coords = inv_M @ coords
# 归一化齐次坐标
source_x = source_coords[0] / source_coords[2]
source_y = source_coords[1] / source_coords[2]
# 重塑为图像尺寸
source_x = source_x.reshape(dst_h, dst_w)
source_y = source_y.reshape(dst_h, dst_w)
# 双线性插值
print("进行双线性插值...")
for c in range(channels):
output[:, :, c] = bilinear_interpolation(image[:, :, c], source_x, source_y)
return output.astype(np.uint8)
def compute_perspective_transform(src_points, dst_points):
"""
计算透视变换矩阵
"""
# 构建线性方程组 A * h = b
A = []
for i in range(4):
x, y = src_points[i]
u, v = dst_points[i]
# 对应方程:u = (h11*x + h12*y + h13)/(h31*x + h32*y + h33)
A.append([x, y, 1, 0, 0, 0, -x*u, -y*u, -u])
A.append([0, 0, 0, x, y, 1, -x*v, -y*v, -v])
A = np.array(A)
# 使用SVD求解
U, S, Vt = np.linalg.svd(A)
h = Vt[-1]
# 重塑为3x3矩阵
H = h.reshape(3, 3)
H = H / H[2, 2] # 归一化
return H
def get_dst_size(dst_points):
"""
根据目标点计算目标图像尺寸
"""
x_coords = dst_points[:, 0]
y_coords = dst_points[:, 1]
width = int(np.max(x_coords) - np.min(x_coords))
height = int(np.max(y_coords) - np.min(y_coords))
return height, width
def bilinear_interpolation(image, x_coords, y_coords):
"""
双线性插值
"""
h, w = image.shape
output = np.zeros_like(x_coords)
# 找到有效的坐标范围
valid_mask = (x_coords >= 0) & (x_coords < w-1) & (y_coords >= 0) & (y_coords < h-1)
# 获取有效坐标
valid_x = x_coords[valid_mask]
valid_y = y_coords[valid_mask]
if len(valid_x) == 0:
return output
# 计算整数和小数部分
x0 = np.floor(valid_x).astype(int)
y0 = np.floor(valid_y).astype(int)
x1 = x0 + 1
y1 = y0 + 1
# 确保坐标在有效范围内
x1 = np.clip(x1, 0, w-1)
y1 = np.clip(y1, 0, h-1)
# 计算权重
dx = valid_x - x0
dy = valid_y - y0
# 双线性插值
interpolated = (image[y0, x0] * (1-dx) * (1-dy) +
image[y0, x1] * dx * (1-dy) +
image[y1, x0] * (1-dx) * dy +
image[y1, x1] * dx * dy)
output[valid_mask] = interpolated
return output
if __name__ == "__main__":
try:
# 使用PIL读取图像
pil_image = Image.open("/Users/admin/Documents/444.jpeg")
img = np.array(pil_image)
if len(img.shape) == 3:
h, w, ch = img.shape
else:
img = np.expand_dims(img, axis=2)
h, w, ch = img.shape
print(f"原图像尺寸: {h}x{w}x{ch}")
# 源数据图取大概一个梯形形状
src = np.float32([[474, 100], [1659, 100], [0, 1200], [1896, 1200]])
dst = np.float32([[0, 0], [2300, 0], [0, 2400], [2300, 2400]])
print("源点坐标:")
print(src)
print("目标点坐标:")
print(dst)
# 应用透视变换
print("正在进行透视变换...")
start_time = time.time()
transformed_img = perspective_transform_numpy(img, src, dst)
end_time = time.time()
print(f"变换耗时: {end_time - start_time:.3f} 秒")
# 转换图像格式用于opencv显示 (RGB -> BGR)
if ch == 3:
img_bgr = cv2.cvtColor(img, cv2.COLOR_RGB2BGR)
transformed_img_bgr = cv2.cvtColor(transformed_img, cv2.COLOR_RGB2BGR)
else:
img_bgr = img
transformed_img_bgr = transformed_img
# 使用opencv显示图像
cv2.namedWindow('Original Image', cv2.WINDOW_NORMAL)
cv2.namedWindow('Perspective Transformed Image', cv2.WINDOW_NORMAL)
cv2.imshow('Original Image', img_bgr)
cv2.imshow('Perspective Transformed Image', transformed_img_bgr)
print("按任意键关闭窗口...")
cv2.waitKey(0)
cv2.destroyAllWindows()
# 保存变换后的图像
output_pil = Image.fromarray(transformed_img)
output_path = "/Users/admin/Documents/444_perspective_transformed.jpeg"
output_pil.save(output_path)
print(f"变换后的图像已保存到: {output_path}")
except FileNotFoundError:
print("错误: 找不到图像文件 /Users/admin/Documents/444.jpeg")
print("请确保图像文件存在,或修改文件路径")
except Exception as e:
print(f"处理图像时发生错误: {e}")
我们用这个图来解释一下上面的代码,愿图像中的4个点相当于上图中ABC所在的物体平面,目标图像中的4个点相当于投影平面A'B'C'。这里的投影中心是虚拟的,一般认为在无穷远点。构建透视变换矩阵的这段代码
def compute_perspective_transform(src_points, dst_points):
"""
计算透视变换矩阵
"""
# 构建线性方程组 A * h = b
A = []
for i in range(4):
x, y = src_points[i]
u, v = dst_points[i]
# 对应方程:u = (h11*x + h12*y + h13)/(h31*x + h32*y + h33)
A.append([x, y, 1, 0, 0, 0, -x*u, -y*u, -u])
A.append([0, 0, 0, x, y, 1, -x*v, -y*v, -v])
A = np.array(A)
# 使用SVD求解
U, S, Vt = np.linalg.svd(A)
h = Vt[-1]
# 重塑为3x3矩阵
H = h.reshape(3, 3)
H = H / H[2, 2] # 归一化
return H
首先我们知道归一化的透视变换方程
- \(x''=\frac {x'}{w}=\frac {a_{11}x+a_{12}y+b_1}{c_0x+c_1y+1}\)
- \(y''=\frac {y'}{w}=\frac {a_{21}x+a_{22}y+b_2}{c_0x+c_1y+1}\)
但在此之前,我们得到的是未归一化的透视变换方程
- \(u=\frac {x'}{w}=\frac {a_{11}x+a_{12}y+b_1}{c_0x+c_1y+d}\)
- \(v=\frac {y'}{w}=\frac {a_{21}x+a_{22}y+b_2}{c_0x+c_1y+d}\)
这里的u和v表示还未归一化的坐标值。整理得到
- \(a_{11}x+a_{12}y+b_1-c_0xu-c_1yu-du=0\)
- \(a_{21}x+a_{22}y+b_2-c_0xv-c_1yv-dv=0\)
由于代码中有4个点,于是就构成了8个方程组成的方程组
- \(a_{11}x_1+a_{12}y_1+b_1-c_0x_1u_1-c_1y_1u_1-du_1=0\)
- \(a_{21}x_1+a_{22}y_1+b_2-c_0x_1v_1-c_1y_1v_1-dv_1=0\)
- \(a_{11}x_2+a_{12}y_2+b_1-c_0x_2u_2-c_1y_2u_2-du_2=0\)
- \(a_{21}x_2+a_{22}y_2+b_2-c_0x_2v_2-c_1y_2v_2-dv_2=0\)
- \(a_{11}x_3+a_{12}y_3+b_1-c_0x_3u_3-c_1y_3u_3-du_3=0\)
- \(a_{21}x_3+a_{22}y_3+b_2-c_0x_3v_3-c_1y_3v_3-dv_3=0\)
- \(a_{11}x_4+a_{12}y_4+b_1-c_0x_4u_4-c_1y_4u_4-du_4=0\)
- \(a_{21}x_4+a_{22}y_4+b_2-c_0x_4v_4-c_1y_4v_4-dv_4=0\)