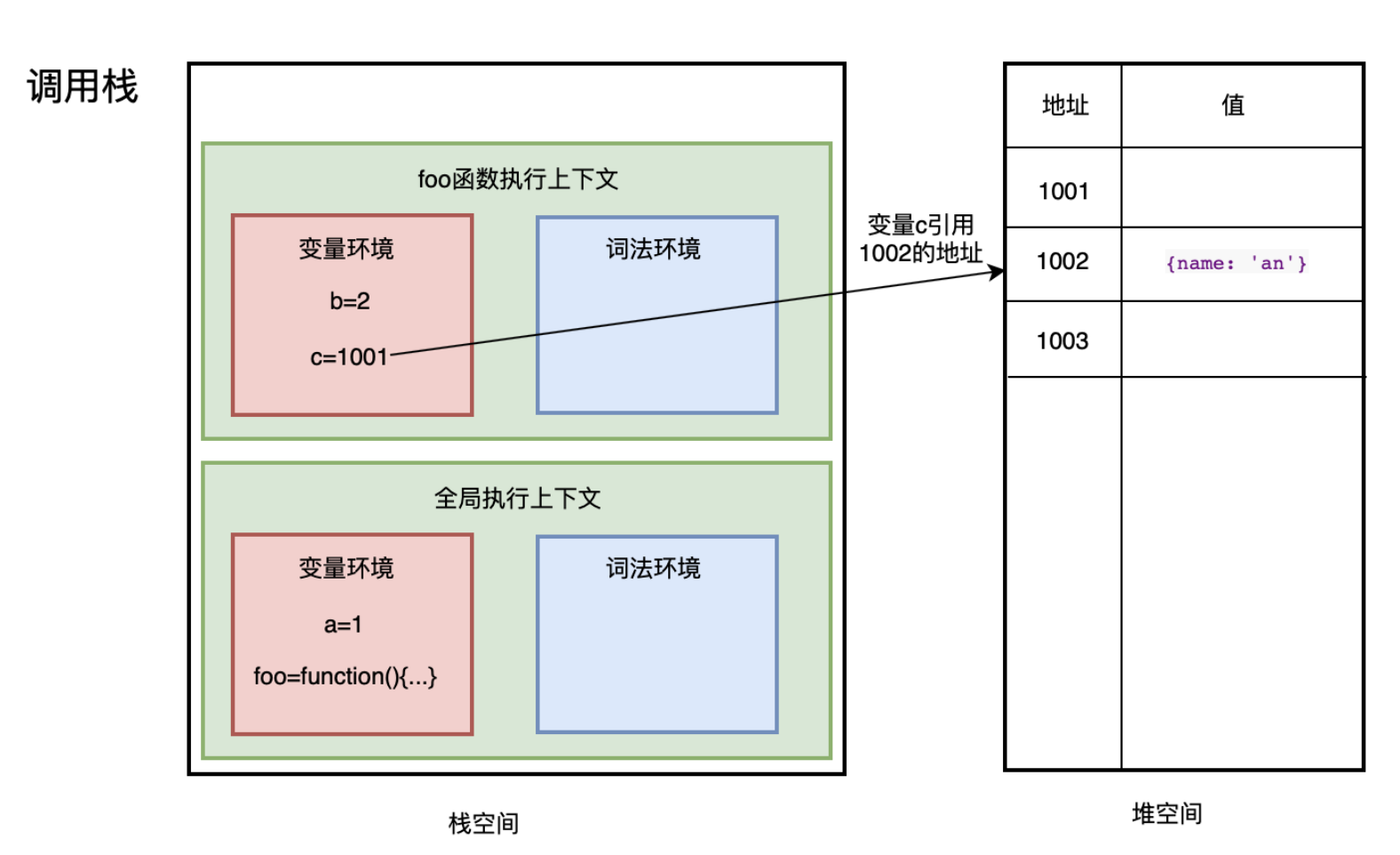
JS的内存空间主要分为代码空间、栈空间和堆空间，代码空间用于存放可执行代码，栈空间用于存放大小固定的数据。当调用栈完成当前的执行上下文时，需要进行垃圾回收，会触发JS的垃圾回收器自动回收，其主要分为栈空间回收和堆空间回收

• 存放在栈空间的数据通过移动ESP指针回收
• 存放在堆空间的数据通过副垃圾回收器(新生代) 和 主垃圾回收器(老生代) 进行回收

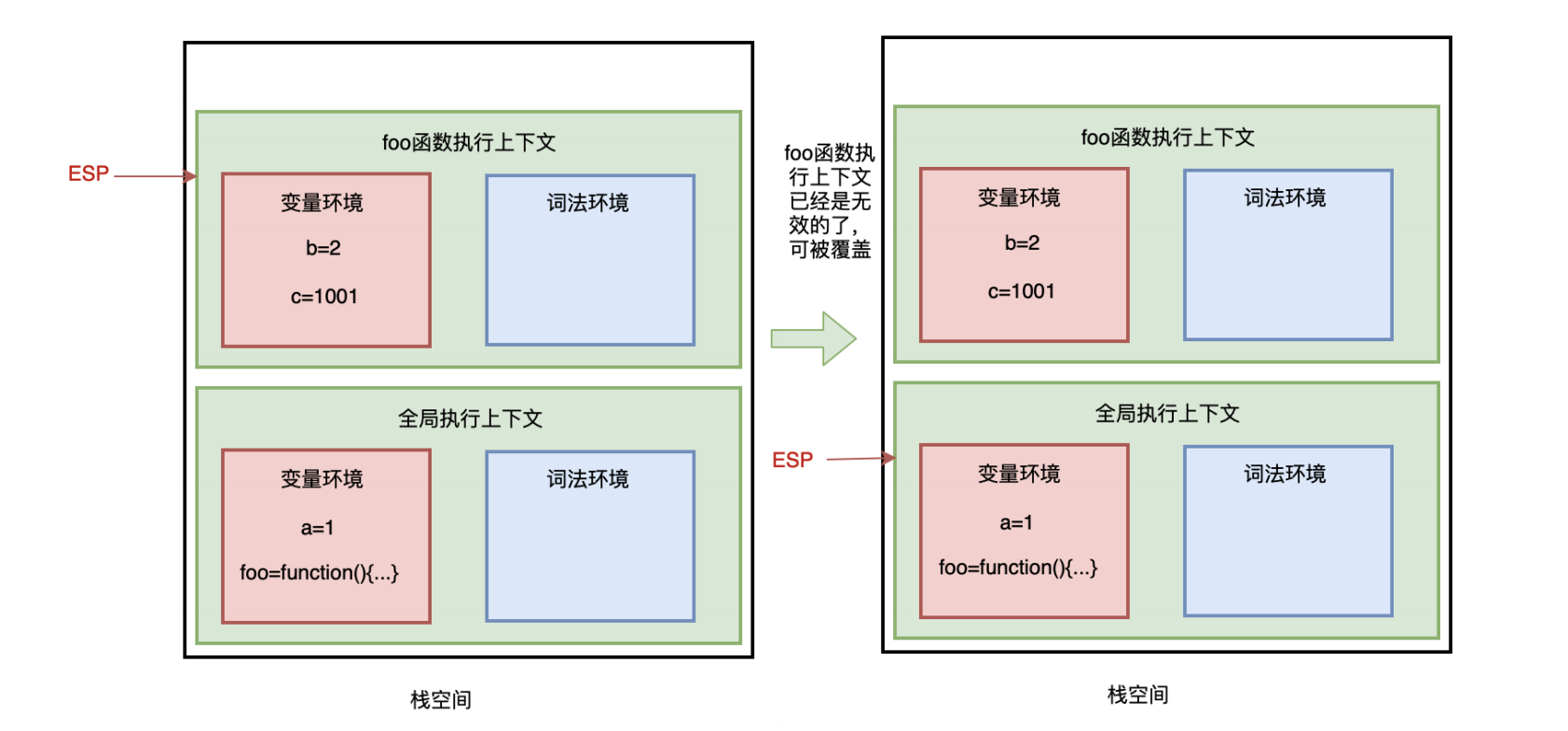
1、栈空间回收

JS 执行代码时，主线程上会存在ESP指针，指向调用栈当前正在执行的上下文，当ESP指针向下移动时，JS引擎会销毁存放在栈空间无效的执行上下文

2、堆空间回收

V8 把堆空间分成新生代和老生代两个区域，新生代用来存放生存周期较短的对象，一般只支持1-8M的容量，而周期较长、容量较大的对象则存放在老生代

两块区域使用了不同的回收器，但流程是相同的

• 标记：是否活动对象
• 垃圾清理：回收非活动对象的内存空间
• 内存整理：内存碎片

2.1、副垃圾回收器

它采⽤ Scavenge 算法及对象晋升策略来进⾏垃圾回收

2.2.1、Scavenge 算法

把新生代空间划分为对象区域和空闲区域，对区域内的对象进行标记，接着将对象区域活动对象有序地复制到空闲区域，完成之后两个区域进行翻转

2.2.2、对象晋升策略

新生代区域很小，因此只要对象经过两次垃圾回收之后依旧存活，就会被晋升到老生代区域

2.2、主垃圾回收器

它主要采用增量标记算法，把垃圾回收拆成一个个小任务，穿插在JS中执行，进而防止垃圾回收执行打断了JS的运行，导致的页面卡顿问题

二、常见题

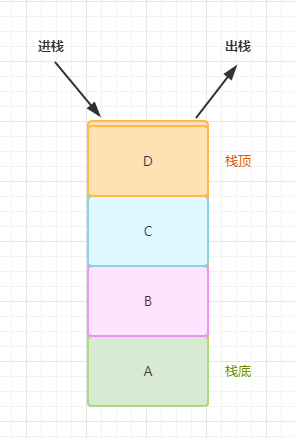
1、栈

栈结构是满足后进先出原则的有序集合，主要的操作有：进栈、出栈 和 清除

1.1、最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈，实现 MinStack 类:

MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素

思路：

• 检索最小元素的时间复杂度要求O(1)，可以通过创建辅助栈，同步主栈操作，也可以直接保存一个最小值变量

const MinStack = function () {
  this.items = []
  this.min = null
};
// 进栈，比较最小元素
MinStack.prototype.push = function (x) {
  if (!this.items.length) this.min = x
  this.min = Math.min(x, this.min)
  this.items.push(x)
};
// 出栈，重新检索最小元素
MinStack.prototype.pop = function () {
  let num = this.items.pop()
  this.min = Math.min(...this.items)
  return num
};
// 获取栈顶元素
MinStack.prototype.top = function () {
  return this.items[this.items.length - 1] || null
};
// 检索栈中的最⼩元素
MinStack.prototype.getMin = function () {
  return this.min
};

1.2、有效的括号

给定一个只包括 (，)，{，}，[，] 的字符串 s ，判断字符串是否有效，有效字符串满足：

• 左括号必须用相同类型的右括号闭合
• 左括号必须以正确的顺序闭合

示例：
    输入：s = "([)]"
    输出：false
    输入：s = "()[]{}"
    输出：true

思路：

• 左右括号是成对的，把左括号放进栈内，遇到右括号时便出栈匹配

var isValid = function (s) {
  const map = { '(': ')', '{': '}', '[': ']' };
  const stack = []
  for (let i of s) {
    if (map[i]) {
      stack.push(map[i])
    } else if (stack.pop() !== i) {
      return false
    }
  }
  return !stack.length
}

1.3、删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。在 S 上反复执行重复项删除操作，直到无法继续删除。在完成所有重复项删除操作后返回最终的字符串。答案保证唯一

示例：
  输入："abbaca"
  输出："ca" // 可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"

思路：

• 入栈之前判断与栈顶是否一致，若一致，则删除栈顶且不进栈，否则进栈

var removeDuplicates = function (s) {
  const stack = [];
  for (let i of s) {
    if (stack[stack.length - 1] === i) {
      stack.pop()
    } else {
      stack.push(i)
    }
  }
  return stack.join('')
};

1.4、删除字符串中的所有相邻重复项II

给你一个字符串 s，k 倍重复项删除操作将会从 s 中选择 k 个相邻且相等的字母，并删除它们，使被删去的字符串的左侧和右侧连在一起。你需要对 s 重复进行无限次这样的删除操作，直到无法继续为止，在执行完所有删除操作后，返回最终得到的字符串

输入：s = "deeedbbcccbdaa", k = 3
输出："aa" // 先删除 "eee" 和 "ccc"，得到 "ddbbbdaa" 再删除 "bbb"，得到 "dddaa" 最后删除 "ddd"，得到 "aa"

思路：

• 扫描字符串依次入栈，入栈前判断是否一致
  • 不一致则入栈
  • 一致，则判断栈顶元素长度是否为k-1，若是则加入该字符就满足条件，因此栈顶出栈，若小于，则取出栈顶元素，加上当前元素

var removeDuplicates = function (s, k) {
  const stack = [];
  for (let i of s) {
    // 取出栈顶，默认满足条件
    let cur = stack.pop()
    // 小心哦，这里cur可能是多个字符啦
    if (!cur || cur[0] !== i) {
      // 错杀了，赶紧重新进栈
      stack.push(cur)
      stack.push(i)
    } else if (cur.length < k - 1) {
      // 还不够资格，悄咪咪回来
      stack.push(cur + i)
    }
  }
  return stack.join('')
}

1.5、删除字符串中出现次数 >= 2 次的相邻字符

与上一题类似，不一样的地方是这里没有明确的边界k，不能确定会重复多少次

示例：
  输⼊："abbbaca"
  输出："ca" // "abbbaca" => "aaca"=>"ca"

思路：

• 创建辅助栈，存储当前没有重复的元素
• 扫描字符串，若遇到同栈顶元素一样的，则至少出现>=2次，辅助栈出栈，移动扫描指针指向下一个不同的元素
• 扫描结束，辅助栈的元素就是结果

function removeDuplicate(s) {
  // 声明辅助栈
  const stack = []
  // 声明栈顶和指针
  let top, next;
  let i = 0;
  while (i < s.length) {
    top = stack.length > 0 ? stack[stack.length - 1] : null;
    next = s[i]
    // 当前字符串与辅助栈栈顶元素相同
    if (next === top) {
      // 出栈
      stack.pop()
      // 移动当前指针到与此栈顶不一致的元素上
      while (s[i] === top) i++
    } else {
      stack.push(next)
      i++
    }
  }
  return stack.join('')
}

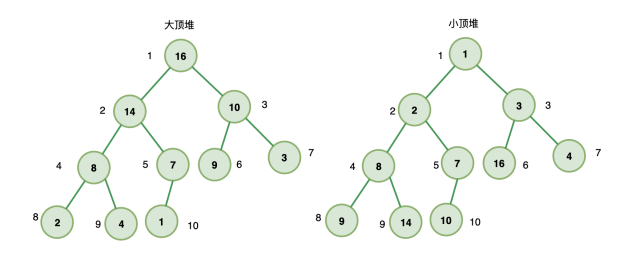
2、堆

堆是一个完全二叉树，在大顶堆中，堆上的任意节点值都必须大于其左右子节点值，小顶堆则反之

2.1、创建顶堆

堆可以用一个数组表示，给定一个节点的下标i(i从1开始)，那么它的父节点一定为A[i/2]，左子节点为A[2i]，右子节点为A[2i+1]

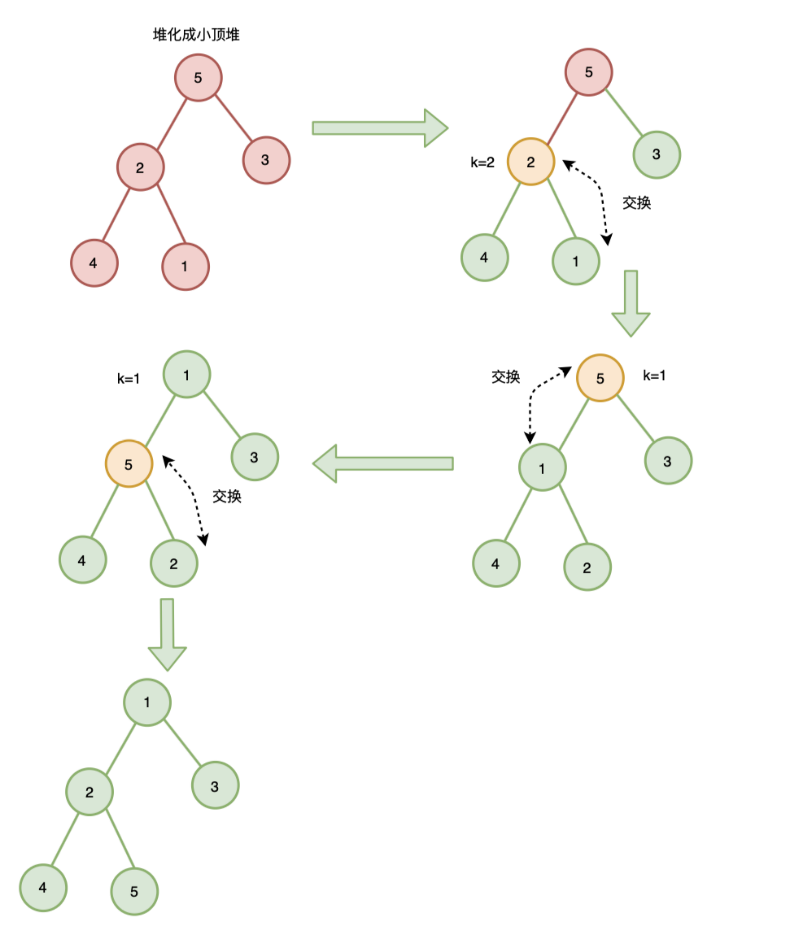
2.1.1、自上而下堆化：调整节点与其左右子节点

从数组最后一个元素开始扫描，即从叶节点一直上溯到根节点，堆化从最后一个非叶子节点开始(n/2)，其时间复杂度为O(nlogn)

const heapify = (items, headSize, i) => {
  while (true) {
    // 小堆里最小值的索引
    let minIndex = i;
    // 左节点存在且根节点小于左节点，则交换
    if (2 * i <= headSize && items[i] > items[2 * i]) minIndex = 2 * i;
    // 右节点存在且根节点小于右节点，则交换
    if (2 * i + 1 <= headSize && items[minIndex] > items[2 * i + 1]) minIndex = 2 * i + 1;
    // 本身最小值则退出
    if (minIndex === i) break;
    // 最小值非本身则交换
    [items[i], items[minIndex]] = [items[minIndex], items[i]]
    i = minIndex
  }
}

const buildHeap = (items, headSize) => {
  // 从最后一个非叶子节点开始，即最后一个子节点的父节点n/2开始
  for (let i = Math.floor(headSize / 2); i >= 1; i--) {
    heapify(items, headSize, i)
  }
}
// 从最后一个元素开始扫描
buildHeap(items, items.length - 1) 

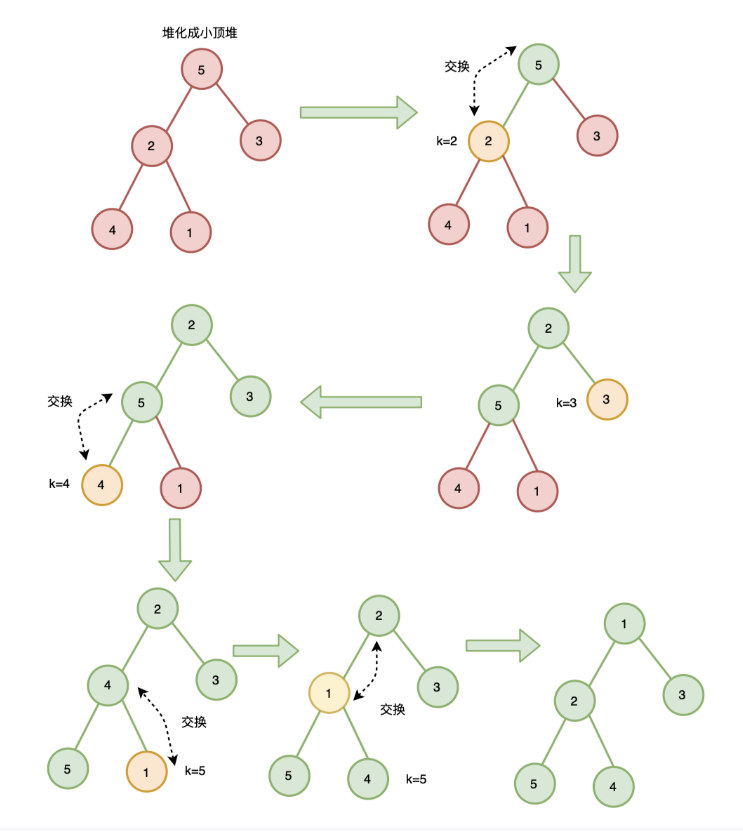
2.1.2、自下而上堆化：调整节点与父节点

从数组第一个元素开始扫描，即从根节点开始，一直向下交换直到叶子节点，其时间复杂度为O(n)

const heapify = (items, i) => {
  // [i]大于[i/2]是大顶堆，小于则小顶堆
  while (Math.floor(i / 2) > 0 && items[i] < items[Math.floor(i / 2)]) {
    [items[i], items[Math.floor(i / 2)]] = [items[Math.floor(i / 2)], items[i]]
    i = Math.floor(i / 2)
  }
}

const buildHeap = (heapItems, heapSize) => {
  while (heapSize < heapItems.length - 1) {
    heapSize++;
    heapify(heapItems, heapSize)
  }
}
// 从第一个元素开始扫描
buildHeap(items, 1) 

2.1、数组中的第K个最大元素

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素

示例：
  输入: [3,2,1,5,6,4] 和 k = 2
  输出: 5

• 建小顶堆，即将输入的乱序数组转换为偏序的二叉堆；
• 依次从堆中取出最小值，插入至有序区域，即可完成排序
• 返回第k个元素即可

时间复杂度：扫描数组O(n)+ 堆化O(logK) => TopK问题-堆解决方案的时间复杂度是O(nlogK) 适用于动态数组

// 小顶堆
const heapify = (heap, k, i) => {
  while (true) {
    let minIndex = i;
    if (2 * i <= k && heap[i] > heap[2 * i]) minIndex = 2 * i;
    if (2 * i + 1 <= k && heap[minIndex] > heap[2 * i + 1]) minIndex = 2 * i + 1;
    if (minIndex === i) break;
    [heap[i], heap[minIndex]] = [heap[minIndex], heap[i]]
    i = minIndex;
  }
}
const buildHeap = (heap, k) => {
  for (let i = Math.floor(k / 2); i >= 1; i--) {
    heapify(heap, k, i)
  }
}
var findKthLargest = function (nums, k) {
  // 堆有效长度最小为1
  const heapNums = [...[,], ...nums];
  let heapSize = heapNums.length - 1;
  buildHeap(heapNums, heapSize);
  while (heapSize) {
    // 最后一个有效元素与第一个最小元素交换，即有序的保存了元素
    [heapNums[1], heapNums[heapSize]] = [heapNums[heapSize], heapNums[1]]
    // 有效序列⻓度减 1
    heapSize--;
    // 重新堆化第一个元素
    heapify(heapNums, heapSize, 1)
  }
  return heapNums[k]
};

2.2、前 K 个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案

示例：
  输入: nums = [1,1,1,2,2,3], k = 2
  输出: [1,2]

思路：

• 利用Map扫描数组并记录对应的频率
• 构建一个k个元素的小顶堆，扫描Map元素，若大于堆顶元素，则与堆顶元素替换，否则继续扫描

const heapify = (heap, map, heapSize, i) => {
  while (true) {
    let minIndex = i;
    // 当前节点大于左节点，交换
    if (2 * i <= heapSize && map.get(heap[i]) > map.get(heap[2 * i])) minIndex = 2 * i;
    // 当前最小节点大于右节点，交换
    if (2 * i + 1 <= heapSize && map.get(heap[minIndex]) > map.get(heap[2 * i + 1])) minIndex = 2 * i + 1;
    if (minIndex === i) break;
    [heap[i], heap[minIndex]] = [heap[minIndex], heap[i]];
    i = minIndex
  }
}
const buildHeap = (heap, map, heapSize) => {
  for (let i = Math.floor(heapSize / 2); i >= 1; i--) {
    heapify(heap, map, heapSize, i)
  }
}

var topKFrequent = function (nums, k) {
  const map = new Map()
  // 扫描累计
  nums.map(num => map.set(num, map.has(num) ? map.get(num) + 1 : 1))
  if (map.size <= k) return [...map.keys()]
  // 遍历扫描结果
  let index = 1
  const heap = [,]
  map.forEach((value, key) => {
    if (index <= k) {
      heap.push(key)
      index === k && buildHeap(heap, map, k)
    } else if (value > map.get(heap[1])) {
      // 替换并堆化
      heap[1] = key
      heapify(heap, map, k, 1)
    }
    index++
  })
  return heap.slice(1);
}

2.4、数据流的中位数

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。例如

  [1,2,3,4,5] => 3             // 当 n % 2 !== 0，middleIndex = arr[(n-1)/2]
  [1,2,3,4,5,6] => (3+4)/3=3.5 // 当 n % 2 === 0，middleIndex = (arr[n/2] + arr[n/2 + 1])/2

设计一个支持以下两种操作的数据结构：

• void addNum(int num) - 从数据流中添加一个整数到数据结构中。
• double findMedian() - 返回目前所有元素的中位数

如果数据流中 99% 的整数都在 0 到 100 范围内，你将如何优化你的算法？

addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2

思路：

• 创建两个堆，大顶堆存储前面较小的数据，小顶堆存储后面较大的数据

• 插入元素时，若小于大顶堆堆顶，则加入大顶堆，否则进入小顶堆。插入后，需保证大小堆达到平衡，即大小堆元素大小相差<=1

• 插入后不平衡时，堆顶元素移动到另一个堆中，直到满足条件

时间复杂度：插入的时间复杂度是O(logK)，求中位数只需返回堆顶元素O(1) => 中位数问题-堆解决方案的时间复杂度是O(logK)

// ⼩顶堆
const minHeap = buildHeap(false)
// ⼤顶堆
const maxHeap = buildHeap(true)

const MedianFinder = function () {
  this.maxHeap = new maxHeap() // ⼤顶堆，保存较小的数据 
  // ⼩顶堆，保存较大的数据
  this.minHeap = new minHeap()
};
// 插⼊元素
MedianFinder.prototype.addNum = function (num) {
  // 若大顶堆无数据、插入元素小于大顶堆堆顶元素，即该元素属于较小数据，则插入大顶堆
  if (!this.maxHeap.size() || num < this.maxHeap.get()) {
    this.maxHeap.insert(num)
  } else {
    this.minHeap.insert(num)
  }

  // 大小顶堆保持平衡的依据是：大顶堆 顶多大于 小顶堆 1个元素
  if (this.maxHeap.size() - this.minHeap.size() > 1) {
    this.minHeap.insert(this.maxHeap.remove())
  }
  if (this.minHeap.size() > this.maxHeap.size()) {
    this.maxHeap.insert(this.minHeap.remove())  // ⼩顶堆向⼤顶堆迁移
  }
};
// 获取中位数
MedianFinder.prototype.findMedian = function () {
  // n 为偶数，则中位数 = 大小堆堆顶和 / 2
  if (this.maxHeap.size() === this.minHeap.size()) {
    return (this.maxHeap.get() + this.minHeap.get()) / 2
  }
  // n为奇数，则中位数 = 大顶堆堆顶
  return this.maxHeap.get()
};

创建堆的实现代码

// 堆化
const heapify = (heap, i, isMax) => {
  const k = heap.length - 1
  while (true) {
    let index = i
    if (isMax) {
      // 大顶堆
      if (2 * i <= k && heap[i] < heap[2 * i]) index = 2 * i;
      if (2 * i + 1 <= k && heap[index] < heap[2 * i + 1]) index = 2 * i + 1;
    } else {
      // 小顶堆
      if (2 * i <= k && heap[i] > heap[2 * i]) index = 2 * i;
      if (2 * i + 1 <= k && heap[index] > heap[2 * i + 1]) index = 2 * i + 1;
    }
    if (index === i) break;
    [heap[i], heap[index]] = [heap[index], heap[i]];
    i = index;
  }
}

const buildHeap = (isMax) => function () {
  let heap = [,]
  // 堆中元素数ᰁ
  this.size = () => heap.length - 1;
  // 获取堆顶元素
  this.get = () => heap.length > 1 ? heap[1] : null;
  // 插⼊
  this.insert = (key) => {
    heap.push(key)
    // 获取存储位置
    let i = heap.length - 1
    const compare = () => isMax ? heap[i] > heap[Math.floor(i / 2)] : heap[i] < heap[Math.floor(i / 2)]
    while (Math.floor(i / 2) > 0 && compare()) {
      [heap[i], heap[Math.floor(i / 2)]] = [heap[Math.floor(i / 2)], heap[i]]
      i = Math.floor(i / 2);
    }
  }
  // 删除堆头并返回
  this.remove = () => {
    if (heap.length > 1) {
      if (heap.length === 2) return heap.pop()
      let num = heap[1]
      heap[1] = heap.pop()
      heapify(heap, 1, isMax)
      return num
    }
    return null
  }
}