![]()
AV1视频编解码器是一种由开放媒体联盟AOM开发的royalty-free的压缩技术。libaom库是AV1的参考软件,应用各种编码器优化技术来实现更好的编码效率。本次分享,我们邀请到了来自Google 的李博晗,一起来讨论 GOP优化、时域滤波器、libaom库的其他改进以及正在进行的一些工作。
大家好!我是来自Google网络媒体团队的李博晗。今天,我将讨论有关AV1的编码器优化技术。
AV1视频编解码器是一种由开放媒体联盟AOM开发的royalty-free的压缩技术。它于2018年发布,与其前身(VP9)相比,AV1提高了约30%的压缩效率。libaom库是AV1的参考软件,它也是由大量AOM的成员开发的,且它是开源的。libaom库使用了各种编码器优化技术以便达到更好的编码效率。今天,我们将讨论其中的部分技术。
首先我们将讨论GOP优化;接着,我们会讨论时域滤波器;其后,我们还将提到libaom库的其他改进和一些正在进行的工作。
![]()
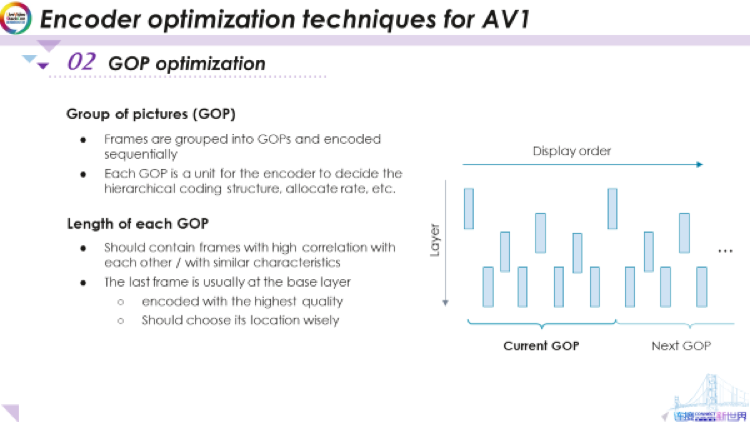
首先是GOP优化,GOP代表图片组(group of picture)。我们要编码的视频序列有很多帧,编码器会将这些帧分组为GOP。然后,编码器将顺序对每个GOP进行编码。基本上GOP是用于决定诸如分层编码结构和码率分配等的基本单元。举一个例子,这是一个包含九帧的GOP。GOP内具有层次结构,基础层一般包括第一帧和最后一帧。可以从这两个帧来预测下一层的帧。而再下一层的帧可以由这个三个帧来预测,以此类推。现在,我们想要确定每个GOP的长度。它的长度非常重要,因为从直觉上来说,我们希望每个GOP中的帧都包含具有相似特征,或者这些帧在GOP内部存在更高的相关性。想要知道GOP的长度,就要确定最后一帧在哪里。通常,最后一帧位于基础层,这意味着它将被用于预测此GOP中存在的所有其他帧。因此,为了提供更好的预测,我们想为最后一帧分配更高的质量。但是,如果我们错误地分配了GOP,例如,这里的最后一帧,如果它位于非常糟糕的位置,与其他帧之间相关性较低(比如GOP停止在场景更改的中间),那么即使我们此帧的重建质量非常高,也不会帮助到其他帧的预测。
2.1 Utilizing first-pass stats
![]()
从直觉出发,我们希望可以确定GOP的长度,使得最后一帧可以更好的预测其他帧。我们可以使用一些自适应方法来确定每个GOP应该多长以及最后一帧应该在哪里。在这里我们使用第一次编码(first-pass)数据。liibom支持两次(two-pass)编码,它先将所有帧编码处理一次,然后收集数据,再重新对所有帧进行编码。第一部分很快,而第二部分才是真正的编码——它使用所有从第一部分收集到的各种帧级别的统计信息。
在这里有三个第一次编码数据的示例,分别是帧内编码错误,一阶编码错误和二阶编码错误。帧内编码错误意味着在从其他帧预测的情况下对该帧进行帧内预测而得到的平均误差。一阶编码错误和我们前面提到的帧内编码错误意义相似,只是我们不仅可以进行帧内编码,还可以进行帧间预测,不过必须通过前一帧。这样,该帧的最大平均预测误差,就是一阶编码错误,二阶编码错误也非常相似。我们仍然可以使用帧内编码或进行帧间预测,但是只能使用相隔两帧的那一帧,这样就得到了二阶编码错误。
拥有这些很多帧级别的特征和数据,我们要使用它们来确定GOP的长度。我们想从这些统计信息中,获悉或者至少估计一下帧之间的相关性,以及其他一些我们关注的特征,并依此来分析第一遍的统计数据。
2.2 The hidden Markov model
![]()
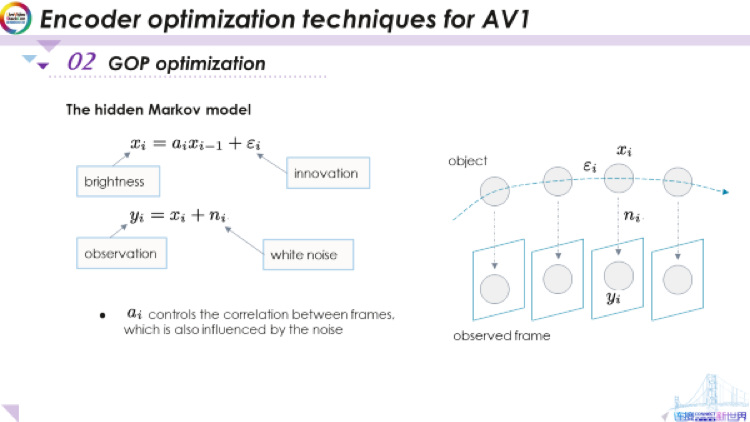
这里,我们使用隐马尔可夫模型(HMM)。该模型假设两件事,首先,它假定基础对象的亮度遵循马尔可夫链。在此示例中,我们可以看这个球,此球沿着这样的轨迹移动。沿着该运动轨迹,我们用xi表示在时间i的亮度。这个模型是一个回归模型,但与自动回归略微有所不同,因为ai会变化。对于xi来说,这是一个马尔可夫链,因为你可以看到 x 在时间 i 的亮度,仅取决于 x 在时间 i-1 的亮度。在此条件下,它与以前所有的亮度都没有关系,这就是马尔可夫模型。
马尔可夫模型已被广泛用于对运动对象在运动轨迹上的建模。这里的ε是创新项(也就是新息),创新项代表xi无法从xi-1中预测的部分。例如,当光逐渐变化,或者物体在其表面上有一些细微的变化时,你将无法得到精确为 1 的相关性,而可能会得到0.95、0.98之类的值,以及这样一个无法预测的创新项。这基本就是我们使用的马尔可夫模型。
应用这里的马尔可夫模型,我们进一步假设当观察物体的亮度时,例如如下所示,捕获每一帧视频时将会捕获到噪声,那些噪声并不依赖于创新项,实际上也与xi无关。它们只是捕获时的加性噪声。在这里用另一个随机变量ni对表示这些噪声。我们假设它是IID(独立同分布)的白噪声。这样我们便得到观察值yi。可以看到,因为噪声的存在,在对事物进行编码时我们根本无法直接得知xi,而只能访问观测值 yi。我们在这里得出的yi以及它背后的模型,这就是一个隐马尔可夫模型,也就是指实际的马尔科夫模型被这种噪声隐藏了。
以上是一个隐马尔科夫模型的非常简单的示例,这就是我们对模型的假设。要注意有两点非常重要,第一是一个重要参数ai。ai基本控制着帧之间的相关性,如果假设xi的方差不变,则ai就是xi和xi-1 之间的相关系数。从我们的出发点来看,我们希望能够估测帧之间的相关性,ai能够帮助我们借用此模型来估测。同时,我们也想了解噪声有多大,从实际情况来看,噪声的方差也很重要。
2.3 Optimal linear prediction error
![]()
我们能观测到在任意的时间点i和j的观测值yi和yj,并希望能够估测ai和噪声。为了能做到这一点,我们首先假设我们使用最优线性预测器,也就是用一个系数w乘以yj来预测yi。如果我们考虑最优线性预测的误差,且使用先前的模型进行计算的话你最终会得到这个等式。此处显示了最佳线性预测误差e^i,j。这个等式是由几个部分组成的。首先,你需要yi和yj的方差,以及从 j 到 i的ak,还需要该帧的噪声的方差。有了这个方程式。回过头来,我们将讨论如何使用它来预测ai。
![]()
让我们来看看,首先,知道在这个方程式中,实际上很多东西可以直接从第一遍统计数据中估算出来。例如yi的方差,也就是观察到的像素方差,可以用帧内编码错误用以近似估计。其背后的原因是,当你进行帧内预测时,可以使用其相邻像素预测该块。然后从该块中移除该预测,这与减去估算出的区块平均值非常相似。这样的话,则帧内编码错误基本上就可以看作像素的方差。这并非完全准确,但非常接近。其后,当j等于i-1时,我们是在从前一帧来预测当前帧。而这恰恰是我们所说的一阶编码错误的含义。同理,如果j等于i-2,最佳线性预测误差就基本可以看作是二阶编码错误。因此,我们使用这三个第一遍统计信息来估测随机变量的这三个特征。我们将获得y的方差,e^i,i-1的方差和e^i,i-2的方差。
2.4 Estimate correlation from first-pass stats
![]()
如果假设所有这些都成立,同时再假设该邻域中的噪声方差不变,即nj的方差在该邻域中保持不变,那么我们可以针对帧i,j写出以下几个等式。一个是从 i-1 预测 i,一个是从i -2预测i-1,还以一个是从i -2预测 i。也就是说我们关心这三个帧,以及其对应的三个预测。现在,如果你写下这三个方程式,你将会发现,实际上我们只有三个未知变量,即ai-1,ai-2,以及该邻域中的噪声方差。因而,基于这三个方程,我们可以很轻松地计算出这三个未知变量。算出之后,也就可以得到ai,aj,可以得到噪声方差。到目前为止,基于此隐马尔可夫模型,我们成功地仅通过第一遍的数据,就能够通过帧邻域来估测帧与帧之间的相关性以及噪声水平。
2.5 Frame regions and GOP length decision
![]()
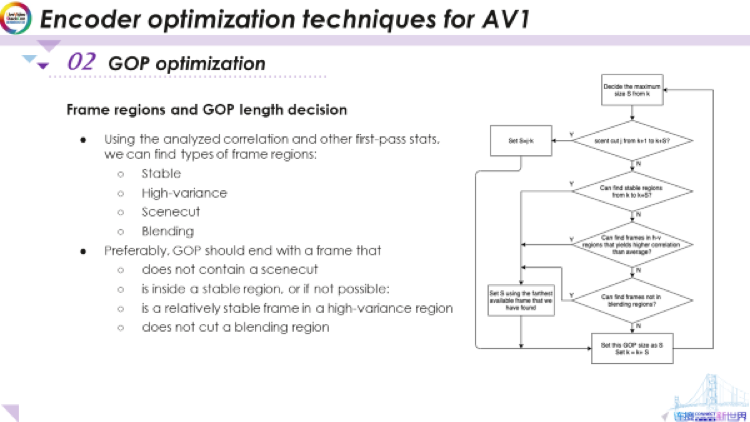
如果现在我们想使用分析出的相关性和噪声水平,来决定GOP长度。首先要做的是确定帧区域的类型,帧可能处于稳定区域或不稳定区域中。我们将不稳定区域分为三种:一种是高变化区域,它其中的帧会变化得较快;一种是场景切换,它会突然改变帧内容;还有一种是渐变区域,这经常出现在电影以及其他内容类型的视频中,一个场景淡出的同时,另一个场景淡入。有了这四种类型的帧区域,首先我们要将每一帧分组到这些区域中。该分组使用前面分析第一遍统计数据得到的ai,噪声水平和其他数据。
![]()
有了这些帧区域后,我们希望最终决定的GOP不包括场景切换,也就是不在一组图片中改变场景。同时还希望该GOP的最后一帧找到处于稳定区域,这背后的原因是,如果它在稳定区域中,则意味着它可以很好地预测其相邻帧。这是我们的首选,如果无法在稳定的区域中找到结束帧,我们将尝试在高变化区域内找到相对稳定的帧。同时,我们也要确保我们不会在渐变区域的中间放置最后一帧。因为通过使用双向多参考,实际上可以很好地对渐变区域进行预测。如果我们将其切开,则意味着预测将变得比较难。因而,我们一般希望将渐变区域放入一个单独的GOP中,而不想将它从中切开。可以看到,一旦我们得到所有帧区域,这些逻辑是很简单的。
![]()
此处以流程图形式展示以上的逻辑。在这里我不想再谈得过于深入,但基本逻辑就如我们在这里所描述的这样。
![]()
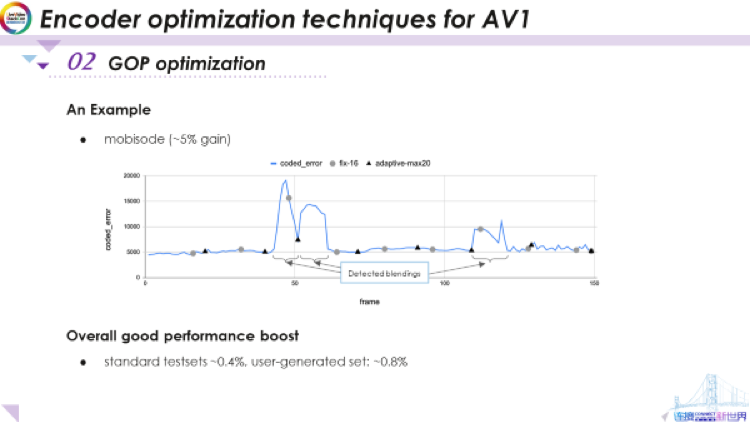
上图是GOP长度优化的一个例子。这里展示了帧的编码错误。这是我们标准测试集中的mobisode视频序列。这些编码错误显示了它与前一帧相比发生了多大变化。你可以看到直到第40帧左右为止它的场景都相当稳定。而在40帧这里实际上是一个场景切换,这是一个渐变场景——实际上视频中的人正在慢慢打开灯,在它(场景)之后这儿又有一个渐变场景。之后一段时间内情况很稳定,然后,就在这里还有另一个渐变场景。之后它会稍微稳定一些,有点高变化,不过并不剧烈。这就是视频序列的情况。
现在看这里的灰色圆圈,这些圆圈是最初由编解码器在没有此自适应GOP技术的情况下完成的GOP长度决策。可以看到实际上切割发生在了该区域的中间。而且就在这个渐变区域的中间,这并不是我们真正想要的。通过自适应方法得到的结果用黑色三角形表示,这是我们实际切割GOP的地方。我们将最大间隙长度设置为20——而之前是固定为16。然后,如你所见,它选择了最佳的切割位置,这是一个GOP,在这里附近切割。不过它没有在渐变区域内切割,以及下在一个渐变区域之前就结束了当前GOP。对于这个序列,如果我们可以像这样准确地切割GOP,我们会得到大约5%的增益,对于仅是更改GOP而言,这是相当大的。
如你所见,此方法可能相当高效,但这具体取决于视频的内容。当然,如果视频非常稳定,则无需在此处进行太多调整,也不会有太多增益。但是如果对于这样具有某些特定特征的序列,你将获得很大增益。标准测试集中我们能看到平均0.4%(已经比较大的)左右的增益,但是在用户生成集中,我们看到的增益更大,约0.8%。因为对于用户生成集而言,大多数视频比标准测试集中的视频更加不稳定,其中有的是通过一直晃动的手机拍摄的,有的是包含像场景剪辑、光线变化之类快速变化的内容。对于它们,自适应GOP方法可以提供更多帮助。以上就是有关libaom编码器中的自适应GOP优化的内容。接下来我们要谈谈时域滤波。
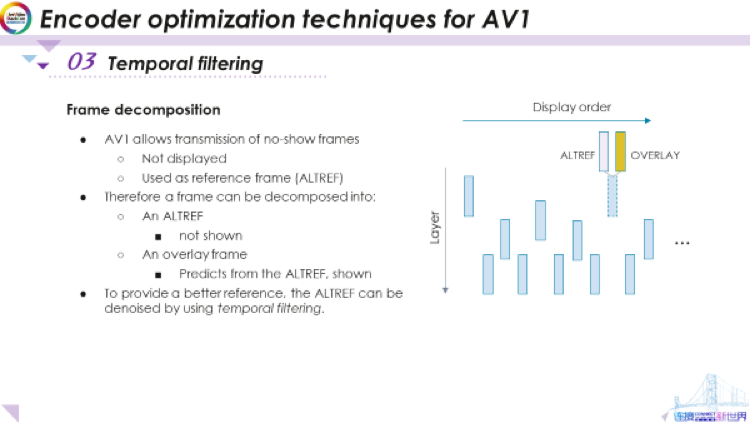
首先我们需要提到AV1中的帧分解。AV1可将一帧分解为一个未显示帧和一个覆盖显示帧。如此处所示,这仍然是我们的GOP。很多时候,GOP的最后一帧,或我们称为ALTREF的帧,会被分解为两帧,一个ALTREF和一个覆盖帧。这里的想法是,我们将对ALTREF进行编码。然后,解码器将解码它,但不会显示,只是将其保存在帧缓冲区中,并用以对其他帧进行预测。之所以要这样做,是因为我们希望能够对该帧进行某些处理,以便其可以为其他帧更好地提供预测。当我们完成了其他帧之后又回到了这一帧时,我们不直接显示该帧,而是再添加一个叠加帧,以修正我们对该帧的处理,这便是覆盖帧的作用。综上所述,我们有一个通常没有显示的替代参考帧ALTREF,根据ALTREF预测我们得到一个覆盖帧,能够修正前面的处理,并且显示出来,这就是每个帧的分解。正如我提到的为了提供更好的预测,我们想对ALTREF进行处理,使其可以很好地预测其他帧,在libaom编码器中可行的一种方法是使用时域滤波器。
3.2 Temporal filtering of a frame
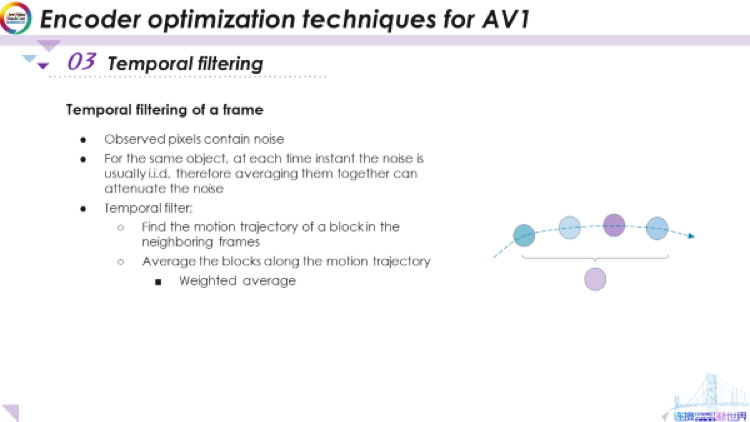
那么,什么是时域滤波器呢?让我们来看看,例如,对于某个像素,假设我要研究该像素的运动轨迹,正如我们前面提到的,运动轨迹存在观察噪声,而我们希望能够滤除该噪声。要做到这一点,我们对该轨迹上的像素进行平均,假设像素实际亮度没有变化,但是存在噪声,那么通过这种方式进行均衡,噪声将有所减少,但像素原始值不会改变。这就是使用时域滤波器来降低噪声的基本想法。时间过滤包含了几个步骤,第一步是通过运动估计及运动搜索来找到运动轨迹。如果我们可以为这些对象的像素块在每一帧中寻找合适的位置,我们就可以对各个块进行平均,以降低噪声水平,从而达到预期的效果。然而,实际上,这并非易事,因为我们需要对所有对象求加权平均值,也就是说需要确定运动规矩上每个像素的权重。我们接下来会讨论这一点。
出于实际考虑,首先,我们并没有真正的运动轨迹,我们能做到的最好就是尝试进行运动估计。而且由于我们只是在处理帧,无法真正执行非常好的运动搜索,而大多数时候只是使用一个快速的算法,因此我们获得的运动轨迹的运动矢量并不总是准确的,甚至有时候很不准确。我们还需要注意的是,过滤后的ALTREF帧并不一定是其他帧中唯一可用的参考帧,它们也可以参考其他可用的参考帧。因此,仅将所有这些像素放在一起求平均可能不是一个好主意,因为某些帧不会用这个参考帧来预测。因而,我们需要慎重考虑设定权重。
为了确定权重,我们提出以下直观原因,首先,如果我们找到一些块的运动轨迹,我们在这个轨迹中找到对应的像素块,然后将该块与帧过滤源进行比较。如果这两个区块彼此之间差异太大,这意味着我们当前的运动矢量非常糟糕,或者我们观测到来非常高的噪声影响,两者皆有可能。如果发生这种情况,我们可能不想为该块分配太高的权重,因为很有可能该块并不会不使用ALTREF作为参考或运动矢量不好,我们也不想冒险。因此我们使用一种称为非局部均值的方法来计算块差异,并确定我们要分配给该块的权重,这是一方面。另一个直观感受是我们想要降低噪声,因此当噪声水平较高时我们就倾向于使用更强的滤波。我们需要能够估计噪声水平,因而,我们在帧内有一个噪声水平估计算法,一旦噪声很高时,我们便使用更强的过滤器。这个噪声水平估计及其影响也被并入我们的非本地均值方法之中。
总体过滤方案如下:首先,我们要确定要使用的相邻帧的数量,这很重要,如果说有一个场景变换,或者说帧之间相关性不是很高,我们将使用更少的帧数。反之,当运动比较稳定时,我们可以使用更多的帧,因为假设运动矢量良好,使用更多的帧可以将噪声控制在较低水平。帧数一旦确定,对于想过滤的帧中的每个块,我们先在相邻帧中找到匹配的块,然后使用非局部均值方法来确定这些帧中每个块的相关权重,接着应用过滤器计算得到所有区块的加权平均值。基本方法就是这样,还有很多细节的内容我们这里不再作介绍。从(这里引用的)文中你可以看到,在标准测试集上,这个方法得到了相当大的增益,约2.4%。因此,在给出更好的预测方面,这种时间过滤器实际上非常有效。以上是时间过滤器相关内容。
以上我们举了两个例子,GOP长度决策和时域滤波器。我们在libaom库中还有很多其他的改进。
首先是运动搜索模式,我们改为使用八边形运动搜索模式。之前我们使用的是棱形或四角搜索,但是现在我们我们使用八边形,它基本上是八点搜索模式,可以更好地适应复杂的角度。而且我们调整了采样半径,之前是2的次方,越远,它越粗糙。但是现在我们对其作了一些微调,并借此获得了一些增益。我们还要注意的另一件事是从最近的报告来看,似乎,复合运动搜索并没有带来先前预期的那般增益。复合模式是我们有多个参考块,然后将参考结合在一起以创建对该区块的预测。大多数的时间它是双向或单向的,我们注意到它并没有像预期的那样带来可观的增益,但是复合运动搜索模式实际上非常强大,它拥有各种模式来适应不同的条件。所以,我们的确寄希望它会有更好的增益,这就是为什么我们最近正在重新设计复合模式的算法。这其中有很多速度方面的功能,现在我们正在尝试重新设计它们。其中一些改变已经在代码中了,并获得不错的增益效果。
另一个非常重要的事是码率控制。目前,码率控制是不易做到的一块。AV1中的原始码率控制方案比较复杂,我们试图简化,重新设计控制逻辑,而且也希望借此获得更好的控制性能,我们不想牺牲任何东西。目前,有严格的码率控制条件时,也就是当码率控制非常准确时,与以前相比,压缩性能比以前变得更好。我们仍在努力使得在某种程度上更宽松的控制情况下它能运行得更好。
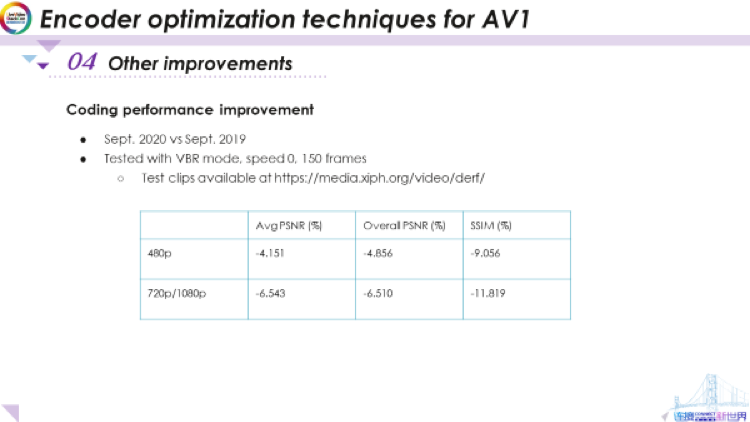
这里展示了编码性能的提高。这是使用VBR模式(可变比特率模式),速度0(这是最高性能),150帧,今年(2020年)9月与去年9月的对比,视频序列可在此处网址上找到。我们测试了很多视频序列,并计算了平均增益。对于480p的中分辨率视频,PSNR的增益约为4-5%,SSIM的增益约为9%。这是相当高的。对于720和1080p这类较高分辨率的视频内容,我们的PSNR增益约为6.5%,而SSIM的增益约为11%至12%。考虑到AV1本身的性能要比vp9约好30%,这些都是相当不错的增益,且仅基于编码器优化。我们认为libaom库的性能还有较大的提升空间,我们也将继续为之努力。
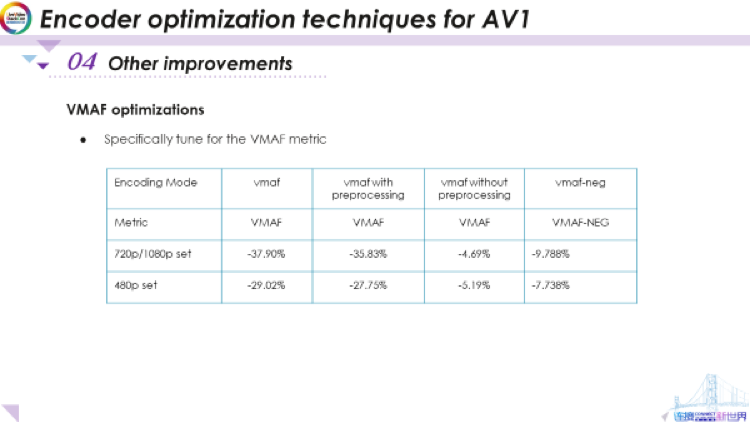
我们还要提到VMAF,这是一项以主观质量为目标的客观质量指标。我们也有一个特定的调优模式,它有命令行选项。如果我们使用VMAF进行调优,我们大约能获得30%到40%的增益,这是巨大的,但这是要通过先对视频进行锐化然后运行所有编码来达到的。如果没有经过预处理,我们将获得大约5%的增益,在没有经过锐化的情况下,这也非常可观了。最近VMAF NEG模式也被提出,在这个模式下我们不过多地专注于预处理导致的影响。不过即使如此,我们的调优模式也可以使它获得大约8%到10%的增益。因此,如果你关心VMAF指标,你可以尝试一下libaom库的这些功能。
还有一点值得注意的,是我们的文档。libaom是一个非常大的代码库,为了可以促进开发者加入贡献,也使其作为参考编码器更容易理解,我们进行了优化文档的工作。首先,我们使用doxygen来从代码注释生成文档。因此,你将获得上层和重要函数的解释和说明,这是可以在编译时生成的。此外,我们还添加了软件开发人员指南,你也可以在代码库中找到(也需使用doxygen)。它包含一些重要的算法流程,例如GOP决策,时域滤波,TPL,码率控制等。如果需要,你也可以参考它们。此外,我们也提交了关于AV1的更详细的综述论文,现在可以在此处的链接查看。
LiveVideoStackCon 2021 ShangHai
LiveVideoStackCon 2021 上海站