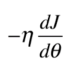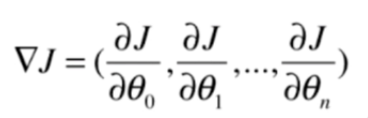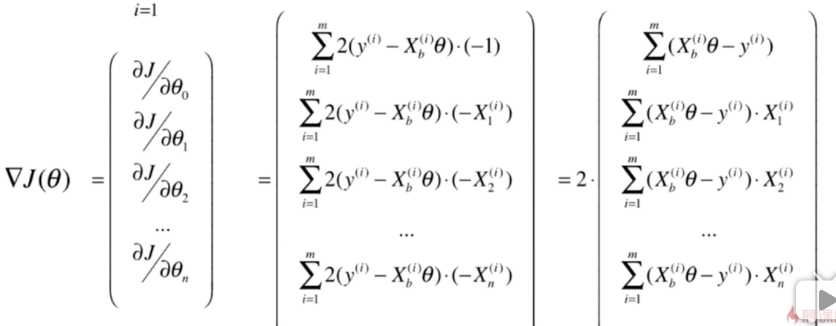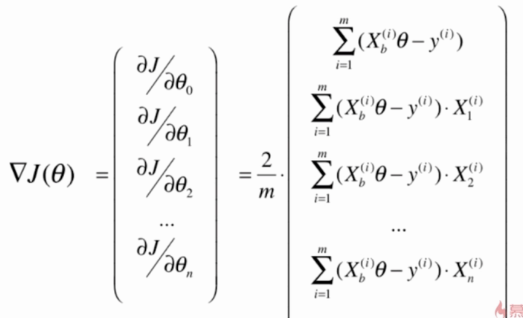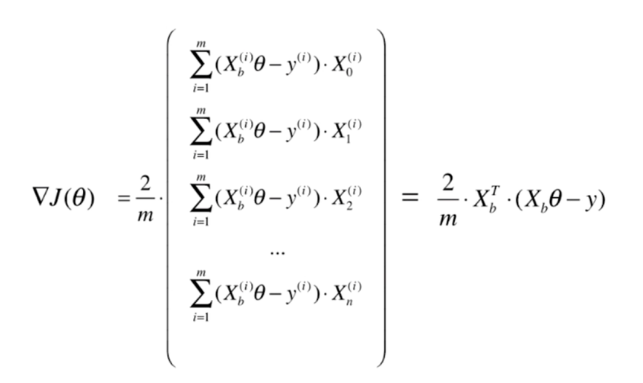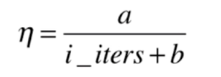梯度下降法不是一种机器学习方法，而是一种基于搜索的最优化方法，它的作用的最小化一个损失函数。相应地，梯度上升可以用于最大化一个效用函数。本文主要讲解梯度下降。

1.批量梯度下降

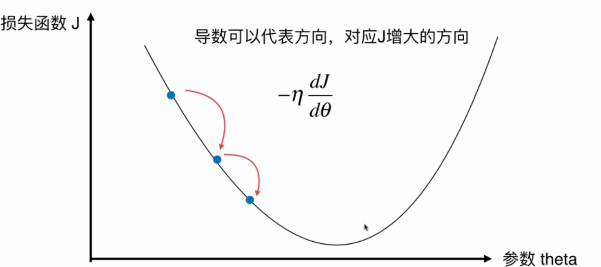
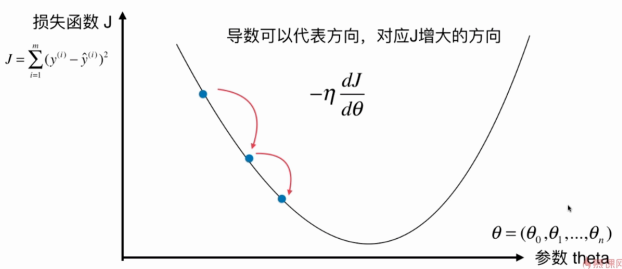
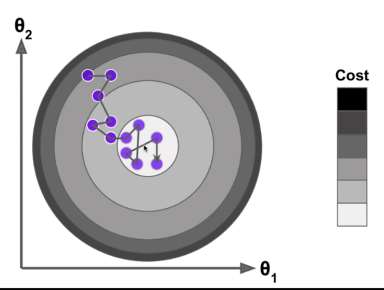
以线性回归为例子，梯度下降法就是不断更新Θ，每次更新的大小就是一个常数乘上梯度。其中这个常数η称为学习率（Learning Rate）。

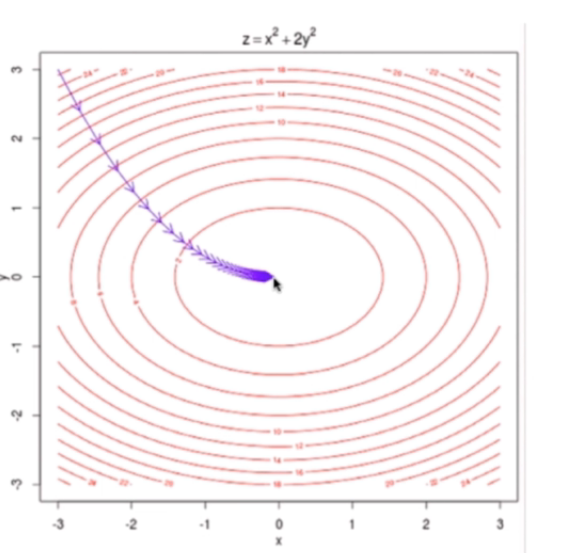
二元时可以把变化趋势图绘制出来。每一个箭头代表一次迭代。

将梯度的每一项写成向量形式

同样的，为了加快训练速度，可以将计算过程向量化

根据之前编写的LinearRegression类，可以用python封装成这种形式

"""
Created by 杨帮杰 on 9/29/18
Right to use this code in any way you want without
warranty, support or any guarantee of it working
E-mail: yangbangjie1998@qq.com
Association: SCAU 华南农业大学
"""

class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def fit_gd(self, X_train, y_train, eta = 0.01, n_iters = 1e4):
        """根据训练数据集X_train, y_train，使用梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
            except:
                return float('inf')

        def dJ(theta, X_b, y):
            # res = np.empty(len(theta))
            # res[0] = np.sum(X_b.dot(theta) - y)
            # for i in range(1, len(theta)):
            #     res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
            # return res * 2 / len(X_b)
            # 进行向量化
            return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(X_b)

        def gradient_descent(X_b, y, inital_theta, eta, n_iters = 1e4, epsilon = 1e-8):

            theta = inital_theta
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta*gradient
                if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break
                cur_iter += 1

            return  theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self


    def predict(self, X_predict):
        """给定待预测数据集X_predict, 返回表示X_predict的结果向量"""
        assert self.interception_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])

        return X_b.dot(self._theta)

    def __repr__(self):
        return "LinearRegression()"

2.随机梯度下降

上面介绍的梯度下降是批量梯度下降（Batch Gradient Descent）。相对地，有另一种方法叫做随机梯度下降（Stochastic Gradient Descent），本质就是随机地选取一个样本点进行一次迭代，然后再随机地选取一个样本点继续迭代。这样做的优势就是——快！

相对于批量梯度下降，随机梯度下降每一次迭代不一定会使损失变小。从统计的意义上讲，他会不断地向settle point附近逼近。实际情况中，往往在极小值附近会有比较大的抖动，而如果η选取过小，前面的迭代学习速度又会过慢。所以，我们在使用随机梯度下降的时候，会使用随着迭代次数而变化的learning rate，如下。

类似地，将下面的方法定义放到LinearRegression类中即可

    def fit_sgd(self, X_train, y_train, n_iters = 1e4, t0 = 5, t1 = 50):
        """根据训练数据集X_train, y_train, 使用随机梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        def dJ_sgd(theta, X_b_i, y_i):
            return X_b_i * (X_b_i.dot(theta) - y_i) * 2

        def sgd(X_b, y, inital_theta, n_iters, t0 = 5,t1 = 50):

            def learning_rate(t):
                return t0 / (t + t1)

            theta = inital_theta
            m = len(X_b)

            for cur_iter in range(n_iters):
                indexes = np.random.permutation(m)
                X_b_new = X_b[indexes]
                y_new = y[indexes]
                for i in range(m):
                    gradient = dJ_sgd(theta, X_b_new[i], y_new[i])
                    theta = theta - learning_rate(cur_iter * m + i) * gradient

            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = zeros(X_b.shape[1])
        self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

sciki-learn中可以这样调用SGDRegression

"""
Created by 杨帮杰 on 10/3/18
Right to use this code in any way you want without
warranty, support or any guarantee of it working
E-mail: yangbangjie1998@qq.com
Association: SCAU 华南农业大学
"""

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler

# 加载波士顿房价的数据集
boston = datasets.load_boston()

# 清除一些不合理的数据
X = boston.data
y = boston.target

X = X[y < 50.0]
y = y[y < 50.0]

# 分离出测试集
X_train, X_test, y_train, y_test = train_test_split(X, y)

# 数据归一化
standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)

# 训练模型
sgd_reg = SGDRegressor(max_iter=100)
sgd_reg.fit(X_train_standard, y_train)

# 打印结果
print(sgd_reg.coef_)
print(sgd_reg.intercept_)
print(sgd_reg.score(X_test_standard, y_test))

结果如下

3.总结

除了批量梯度下降法和随机梯度下降法之外，还有小批量梯度下降法（Mini-Batch gradient descent），方法是随机选取一小批样本进行迭代，原理差不多，这里不再赘述。

相对于使用正规方程解的方式解决线性回归问题，使用梯度下降可以在特征数量比较多的时候有更快的训练速度（比如图像识别）。有的机器学习算法只能使用梯度下降进行优化。

相对于批量梯度下降法，随机梯度下降法的特点：

• 能够跳出局部最优解
• 更快的运行速度
• 结果一般会稍差

损失函数不一定有唯一的极小值点（不一定是凸函数），这时候的解决方案有：

• 多次运行，随机化初始点
• 将初始点的位置作为一个超参数

References:
Python3 入门机器学习 经典算法与应用 —— liuyubobobo
机器学习实战 —— Peter Harrington