简介
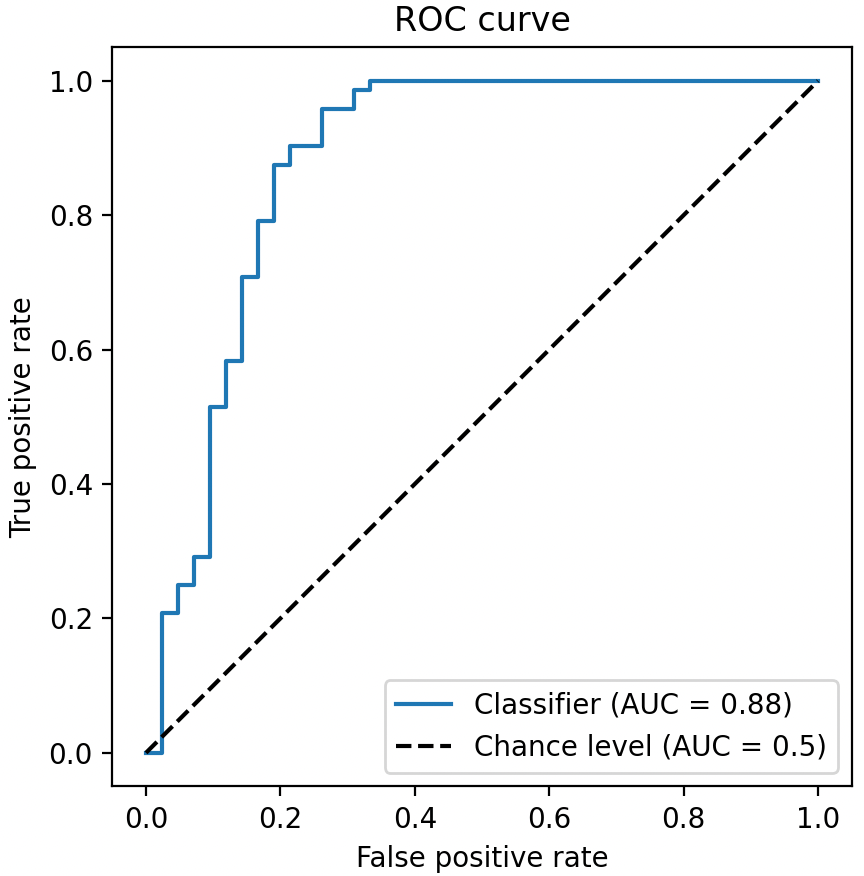
上篇文章 小白也能看懂的 ROC 曲线详解 介绍了 ROC 曲线。本文介绍 AUC。AUC 的全名为Area Under the ROC Curve,即 ROC 曲线下的面积,最大为 1。
![]()
根据 ROC 和 AUC 的关系,我们可以得到如下结论
- ROC 曲线接近左上角 ---> AUC 接近 1:模型预测准确率很高
- ROC 曲线略高于基准线 ---> AUC 略大于 0.5:模型预测准确率一般
- ROC 低于基准线 ---> AUC 小于 0.5:模型未达到最低标准,无法使用
二分类 AUC
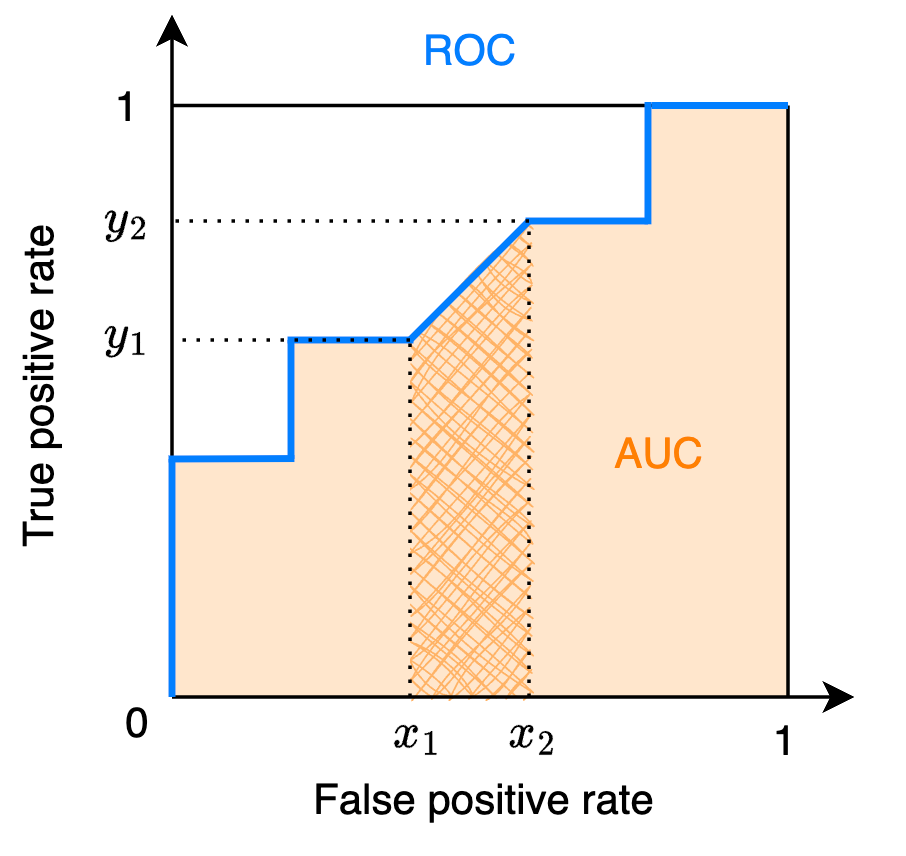
由 AUC 名称可知,可以先计算 ROC 曲线,得到 TPR 和 FPR 的坐标后再分段计算面积即可得到 AUC
![]()
下面是对应的 Python 代码
def auc_from_roc(fpr, tpr):
"""
计算ROC面积
fpr: 从小到大排序的fpr坐标
tpr: 从小到大排序的tpr坐标
"""
area = 0
for i in range(len(fpr) - 1):
area += trapezoid_area(fpr[i], fpr[i + 1], tpr[i], tpr[i + 1])
return area
def trapezoid_area(x1, x2, y1, y2):
"""
计算梯形面积
x1, x2: 横坐标 (x1 <= x2)
y1, y2: 纵坐标 (y1 <= y2)
"""
base = x2 - x1
height_avg = (y1 + y2) / 2
return base * height_avg
也可以直接从真实标签和模型预测分数中计算 ROC,算法的时间复杂度为\(O(n\log n)\),参考文献 1 中的算法 2
# import numpy as np
def auc_binary(y_true, y_score, pos_label):
"""
y_true:真实标签
y_score:模型预测分数
pos_label:正样本标签,如“1”
"""
num_positive_examples = (y_true == pos_label).sum()
num_negtive_examples = len(y_true) - num_positive_examples
tp, fp, tp_prev, fp_prev, area = 0, 0, 0, 0, 0
score = -np.inf
for i in np.flip(np.argsort(y_score)):
if y_score[i] != score:
area += trapezoid_area(fp_prev, fp, tp_prev, tp)
score = y_score[i]
fp_prev = fp
tp_prev = tp
if y_true[i] == pos_label:
tp += 1
else:
fp += 1
area += trapezoid_area(fp_prev, fp, tp_prev, tp)
area /= num_positive_examples * num_negtive_examples
return area
多分类 AUC
现在考虑多分类的情况,假设类别数为\(C\)。
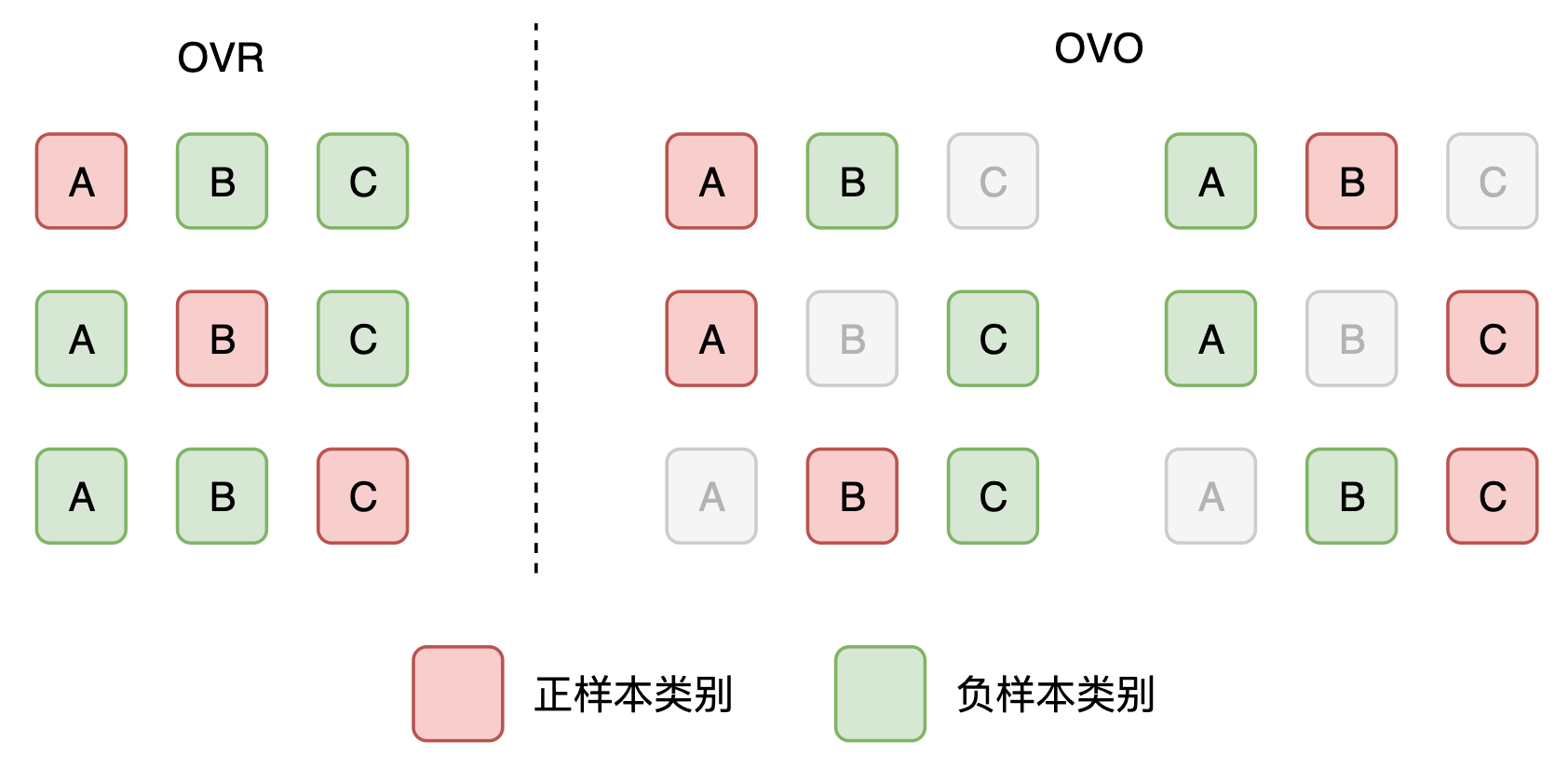
一种想法是将某一类别设为正样本类别,其余类别设为负样本类别,然后计算二分类下的 AUC。这种方法叫做一对多,即 One-Vs-Rest (OVR)。可以得到\(C\)个二分类的 AUC,然后计算平均数得到多分类的 AUC。
另一种想法是将某一类别设为正样本类别,另外一个类别(非自身)设为负样本类别计算二分类的 AUC。这种方法叫做一对一,即 One-Vs-One (OVO)。可以得到\(C(C-1)\)个二分类的 AUC,然后计算平均数。
![]()
当计算平均数时,可以考虑算数平均数(称为 macro),或者加权平均数(称为 weighted)。其中,加权为各类别的样本所占比例。因此,两两组合可以的得到四种计算多分类 AUC 的方法。值得一提的是,知名机器学习库 scikit-learn 的 roc_auc_score 函数 包含了上述四种方法。
- 一对多 + 算数平均数(OVR + macro)
- 一对多 + 加权平均数(OVR + weighted)
- 一对一 + 算数平均数(OVO + macro)
- 一对一 + 加权平均数(OVO + weighted)
一对多 + 算数平均数
多分类 AUC 的计算公式为
\(\text{AUC}_\text{total}=\frac{1}{C}\sum_{c_i\in C}\text{AUC}(c_i)\)
其中\(\text{AUC}(c_i)\)是将类别\(c_i\)作为正样本类别(剩余作为负样本类别),计算的二分类 AUC。
# sklearn.metrics.roc_auc_score(y_true, y_score, average='macro', multi_class='ovr')
def auc_ovr_macro(y_true, y_score):
auc = 0
C = max(y_true) + 1
for i in range(C):
auc += auc_binary(y_true, y_score[:, i], pos_label=i)
return auc / C
一对多 + 加权平均数
多分类 AUC 的计算公式为
\(\text{AUC}_\text{total}=\sum_{c_i\in C}\text{AUC}(c_i)p(c_i)\)
其中,权重\(p(c_i)=\frac{\sum\mathbb{I}\{y=c_i\}}{n}\),即标签为\(c_i\)的样本所占比例,权重之和为 1。
# sklearn.metrics.roc_auc_score(y_true, y_score, average='weighted', multi_class='ovr')
def auc_ovr_weighted(y_true, y_score):
auc = 0
C = max(y_true) + 1
n = len(y_true)
for i in range(C):
p = sum(y_true == i) / n
auc += auc_binary(y_true, y_score[:, i], pos_label=i) * p
return auc
一对一 + 算数平均数
多分类 AUC 的计算公式为
\(\text{AUC}_\text{total}=\frac{2}{C(C-1)}\sum_{{c_i,c_j}\in C,\ c_i<c_j}\text{AUC}(c_i,c_j)\)
其中,\(\text{AUC}(c_i,c_j)=\frac{\text{AUC}(c_i|c_j)+\text{AUC}(c_j|c_i )}{2}\)。即将\(c_i\)作为正样本类别、\(c_j\)作为负样本类别计算二分类 \(\text{AUC}(c_i|c_j)\);然后将\(c_j\)作为正样本类别、\(c_i\)作为负样本类别计算二分类 \(\text{AUC}(c_j|c_i)\)。\(\text{AUC}(c_i,c_j)\) 为其计算的算数平均值。由于将\(c_i\)和\(c_j\)组合计算,共得到 \(C(C-1)/2\) 个二分类 AUC。
# sklearn.metrics.roc_auc_score(y_true, y_score, average='macro', multi_class='ovo')
def auc_ovo_macro(y_true, y_score):
auc = 0
C = max(y_true) + 1
for i in range(C - 1):
i_index = np.where(y_true == i)[0]
for j in range(i + 1, C):
j_index = np.where(y_true == j)[0]
index = np.concatenate((i_index, j_index))
auc_i_j = auc_binary(y_true[index], y_score[index, i], pos_label=i)
auc_j_i = auc_binary(y_true[index], y_score[index, j], pos_label=j)
auc += (auc_i_j + auc_j_i) / 2
return auc * 2 / (C * (C - 1))
一对一 + 加权平均数
多分类 AUC 的计算公式为
\(\text{AUC}_\text{total}=\sum_{{c_i,c_j}\in C,\ c_i<c_j}\text{AUC}(c_i,c_j)p(c_i,c_j)\)
其中,权重\(p(c_i,c_j)=\frac{\sum\mathbb{I}\{y=c_i\}+\sum\mathbb{I}\{y=c_j\}}{(C-1)n}\),即标签为\(c_i\)和\(c_j\)的样本所占比例,分母中的系数 \(C-1\) 使得权重之和为 1。
# sklearn.metrics.roc_auc_score(y_true, y_score, average='weighted', multi_class='ovo')
def auc_ovo_weighted(y_true, y_score):
auc = 0
C = max(y_true) + 1
n = len(y_true)
for i in range(C - 1):
i_index = np.where(y_true == i)[0]
for j in range(i + 1, C):
j_index = np.where(y_true == j)[0]
index = np.concatenate((i_index, j_index))
p = len(index) / n / (C - 1)
auc_i_j = auc_binary(y_true[index], y_score[index, i], pos_label=i)
auc_j_i = auc_binary(y_true[index], y_score[index, j], pos_label=j)
auc += (auc_i_j + auc_j_i) / 2 * p
return auc
参考文献
- Fawcett, Tom. "An introduction to ROC analysis." <em>Pattern recognition letters</em> 27, no. 8 (2006): 861-874. https://www.researchgate.net/profile/Tom-Fawcett/publication/222511520_Introduction_to_ROC_analysis/links/5ac7844ca6fdcc8bfc7fa47e/Introduction-to-ROC-analysis.pdf
- Hand, David J., and Robert J. Till. "A simple generalisation of the area under the ROC curve for multiple class classification problems." <em>Machine learning</em> 45 (2001): 171-186. https://link.springer.com/content/pdf/10.1023/A:1010920819831.pdf
作者:PrimiHub-Kevin