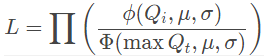优化过程 PK ：Julia 能打败 Python 和 R 笑到最后吗？

在这篇文章中，作者通过一个简单的似然函数优化（Maximum Likelihood Optimization）问题来对比 Julia，R 和 Python。这是一个比较小的优化问题，性能上的差异表现可能不太明显，但解决问题的过程能很好地反应三者各自的优劣势。

作者在撰写本文时，对这三种语言的熟悉程度如下：

语言	实战经验
R	9 年
Julia	6 个月
Python	新手

Julia 布道者 ChrisRackauckas 曾经说过：

如果你用 Julia 处理一个 10 秒内的问题，它的优势并不能体现出来。 而一旦处理的问题变复杂，需要花费比较长的时间，这时 Julia 的优势就会慢慢体现了。

有人用 Python 和 Julia 做过对比实验。以 10⁵ 为界点进行计算，当数值比 10⁵ 更小时 Python 比 Julia 快的。但数值大于 10⁵ 后，Julia 的速度就比 Python 快很多了。

优化问题

观察序列 Q1,Q2,...,Qn，我们需要找到优化该似然函数的参数 μ 和 σ：

通常我们会尝试优化对数似然：

在统计学上，这是截断的正态分布的最大似然估计（MLE）。

Julia 的测试情况

以下是作者使用 Julia 进行测试的情况。使用 Julia 中的 Optim.jl，可以直接使用特殊符号（symbols）作为变量名称，按照使用习惯，此处作者使用了希腊字母 μσ。Julia 还有一个 JuMP.jl 包用于优化问题。但 JuMP.jl 更适合用于更高级的优化问题，用在此处有点小题大做。

Julia 第一次优化

Julia 在执行第一次优化用了 7 秒，比 R 和 Python 都慢。对此，ChrisRackauckas 指出：

如果你需要解决 100 个 10 秒的优化问题，第一次执行需要花费 17 秒，接下来的优化不需要编译，大约只需要 10 秒。因此，总运行时常为 1007 秒。所以，当用 Julia 处理一个 10⁵ 秒的问题时，这 7 秒基本可以忽略不记；但如果用 Julia 处理 5 秒甚至更小的问题时，这 7 秒的差异就特别明显。

作者在下方硬编码了在 MLE 估计中使用的 Q_t 的值：

using Distributions, Optim# hard coded data\observationsodr=[0.10,0.20,0.15,0.22,0.15,0.10,0.08,0.09,0.12] Q_t = quantile.(Normal(0,1), odr)# return a function that accepts `[mu, sigma]` as parameterfunction neglik_tn(Q_t) maxx = maximum(Q_t) f(μσ) = -sum(logpdf.(Truncated(Normal(μσ[1],μσ[2]), -Inf, maxx), Q_t)) f end neglikfn = neglik_tn(Q_t)# optimize!# start searching @time res = optimize(neglikfn, [mean(Q_t), std(Q_t)]) # 7.5 seconds@time res = optimize(neglikfn, [mean(Q_t), std(Q_t)]) # 0.000137 seconds# the \mu and \sigma estimatesOptim.minimizer(res) # [-1.0733250637041452,0.2537450497038758] # or# use `fieldnames(res)` to see the list of field names that can be referenced via . (dot)res.minimizer # [-1.073

输出效果如下，排版看起来很舒服，也支持数学公示显示：

Results of Optimization Algorithm * Algorithm: Nelder-Mead * Starting Point: [-1.1300664159893685,0.22269345618402703] * Minimizer: [-1.0733250637041452,0.2537450497038758] * Minimum: -1.893080e+00 * Iterations: 28 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 59

由此看出 Julia 的优势：

指数	描述
	Truncated(DN, lower, upper) 是定义截断分布的非常简单的方法
	logpdf 函数适用于任何分布式函数
	输出结果条理清晰，可读性强

Julia 的不足：

指数	描述
	如果只是处理 10 秒内的简单问题，7.5 秒的编译时间会很烦人

R 的测试情况

R 有一个 truncnorm 用于处理截断正态

odr=c(0.10,0.20,0.15,0.22,0.15,0.10,0.08,0.09,0.12) x = qnorm(odr) library(truncnorm) neglik_tn = function(x) { maxx = max(x) resfn = function(musigma) { -sum(log(dtruncnorm(x, a = -Inf, b= maxx, musigma[1], musigma[2]))) } resfn } neglikfn = neglik_tn(x) system.time(res <- optim(c(mean(x), sd(x)), neglikfn)) res

结果将输出：

$par [1] -1.0733354 0.2537339 $value [1] -1.89308 $counts function gradient 55 NA $convergence [1] 0 $message NULL

R 的优势：

指数	描述
	又处理截断正态的专用包
	马上输出结果，编译比 Julia 快

R 的不足：

指数	描述
	截断正态没有对数密度; 没有简单的方法来定义任意分布的截断分布; 稀疏输出

Python 的测试情况

作者利用已有的 Python 学习经验想出如下方案，输入代码：

import numpy as npfrom scipy.optimize import minimizefrom scipy.stats import norm# generate the dataodr=[0.10,0.20,0.15,0.22,0.15,0.10,0.08,0.09,0.12] Q_t = norm.ppf(odr) maxQ_t = max(Q_t)# define a function that will return a return to optimize based on the input datadef neglik_trunc_tn(Q_t): maxQ_t = max(Q_t) def neglik_trunc_fn(musigma): return -sum(norm.logpdf(Q_t, musigma[0], musigma[1])) + len(Q_t)*norm.logcdf(maxQ_t, musigma[0], musigma[1]) return neglik_trunc_fn# the likelihood function to optimizeneglik = neglik_trunc_tn(Q_t)# optimize!res = minimize(neglik, [np.mean(Q_t), np.std(Q_t)]) res

输出结果：

 fun: -1.8930804441641282 hess_inv: array([[ 0.01759589, 0.00818596], [ 0.00818596, 0.00937868]]) jac: array([ -3.87430191e-07, 3.33786011e-06]) message: 'Optimization terminated successfully.' nfev: 40 nit: 6 njev: 10 status: 0 success: True x: array([-1.07334252, 0.25373624])

Python 的优势：

指数	描述
	易于学习，各种支持非常好
	能很快输出结果，比 Julia 编译快

Python 的不足：

指数	描述
	输出的可读性有待提高

 综上所述，三种的综合对比如下：

语言	优势	不足
Julia	易于使用；完美支持截断正态分布；可读性强	第一次运行编译时间长
R	易于使用	可读性对比 Julia 较差
Python	易于使用	可读性对比 Julia 较差

相关链接

• Julia 的详细介绍：点击查看
• Julia 的下载地址：点击下载