排序算法（三）冒泡、选择排序的Python实现及算法优化详解

说在前面

最近一年太忙，博客长草了。近日用Python实现了常用排序算法，供大家参考。

Java版本排序算法及优化，请看以前的文章。

《排序算法之简单排序（冒泡、选择、插入）》

《排序算法（二）堆排序》

1、排序概念

这里不再赘述，请参看前面2篇文章

2、简单排序之冒泡法Python实现及优化

原理图

2.1、基本实现

num_list = [     [1, 9, 8, 5, 6, 7, 4, 3, 2],     [1, 2, 3, 4, 5, 6, 7, 8, 9] ] nums = num_list[1] print(nums) length = len(nums) count_swap = 0 count = 0 # bubble_sort for i in range(length):     for j in range(length-i-1):         count += 1         if nums[j] > nums[j+1]:             tmp = nums[j]             nums[j] = nums[j+1]             nums[j+1] = tmp             count_swap += 1 print(nums, count_swap, count)

2.2、优化实现

思路：如果本轮有交互，就说明顺序不对；如果本轮无交换，说明是目标顺序，直接结束排序。

num_list = [     [1, 9, 8, 5, 6, 7, 4, 3, 2],     [1, 2, 3, 4, 5, 6, 7, 8, 9],     [1, 2, 3, 4, 5, 6, 7, 9, 8] ] nums = num_list[2] print(nums) length = len(nums) count_swap = 0 count = 0 # bubble_sort for i in range(length):     flag = False     for j in range(length-i-1):         count += 1         if nums[j] > nums[j+1]:             tmp = nums[j]             nums[j] = nums[j+1]             nums[j+1] = tmp             flag = True # swapped             count_swap += 1     if not flag:         break print(nums, count_swap, count)

总结：

冒泡法需要数据一轮轮比较。

优化，则可设定一个标记判断此轮是否有数据交换发生，如果没有发生交换，可以结束排序，如果发生交换，继续下一轮排序

最差的排序情况是，初始顺序与目标顺序完全相反，遍历次数1,...,n-1之和n(n-1)/2

最好的排序情况是，初始顺序与目标顺序完全相同，遍历次数n-1

时间复杂度O(n^2)

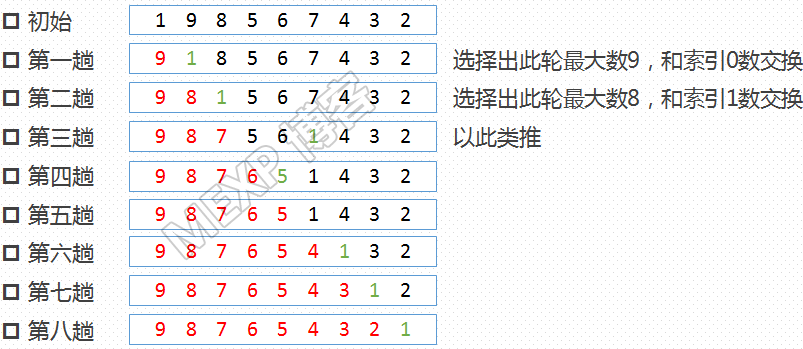
3、简单排序之选择排序Python实现及优化

选择排序的核心：每一轮比较找到一个极值（最大值或最小值）放到某一端，对剩下的数再找极值，直至比较结束。

原理图

3.1、基本实现

m_list = [     [1, 9, 8, 5, 6, 7, 4, 3, 2],     [1, 2, 3, 4, 5, 6, 7, 8, 9],     [9, 8, 7, 6, 5, 4, 3, 2, 1],     [1, 1, 1, 1, 1, 1, 1, 1, 1] ] nums = m_list[0] length = len(nums) print(nums) count_swap = 0 count_iter = 0 for i in range(length):     maxindex = i     for j in range(i + 1, length):         count_iter += 1         if nums[maxindex] < nums[j]:             maxindex = j     if i != maxindex:         tmp = nums[i]         nums[i] = nums[maxindex]         nums[maxindex] = tmp         count_swap += 1 print(nums, count_swap, count_iter)

3.2、优化实现——二元选择排序

思路：减少迭代次数，一轮确定2个数，即最大数和最小数。

m_list = [     [1, 9, 8, 5, 6, 7, 4, 3, 2],     [1, 2, 3, 4, 5, 6, 7, 8, 9],     [9, 8, 7, 6, 5, 4, 3, 2, 1],     [1, 1, 1, 1, 1, 1, 1, 1, 1] ] nums = m_list[3] length = len(nums) print(nums) count_swap = 0 count_iter = 0 # 二元选择排序 for i in range(length // 2):     maxindex = i     minindex = -i - 1     minorigin = minindex          for j in range(i + 1, length - i):  # 每次左右都要少比较一个         count_iter += 1         if nums[maxindex] < nums[j]:             maxindex = j         if nums[minindex] > nums[-j - 1]:             minindex = -j - 1          #print(maxindex,minindex)     if i != maxindex:         tmp = nums[i]         nums[i] = nums[maxindex]         nums[maxindex] = tmp         count_swap += 1         # 如果最小值被交换过，要更新索引         if i == minindex or i == length + minindex:             minindex = maxindex          if minorigin != minindex:         tmp = nums[minorigin]         nums[minorigin] = nums[minindex]         nums[minindex] = tmp         count_swap += 1 print(nums, count_swap, count_iter)

3.3、等值情况优化

思路：二元选择排序的时候，每一轮可以知道最大值和最小值，如果某一轮最大最小值都一样了，说明剩下的数字都是相等的，直接结束排序。

m_list = [     [1, 9, 8, 5, 6, 7, 4, 3, 2],     [1, 2, 3, 4, 5, 6, 7, 8, 9],     [9, 8, 7, 6, 5, 4, 3, 2, 1],     [1, 1, 1, 1, 1, 1, 1, 1, 1] ] nums = m_list[3] length = len(nums) print(nums) count_swap = 0 count_iter = 0 # 二元选择排序 for i in range(length // 2):     maxindex = i     minindex = -i - 1     minorigin = minindex          for j in range(i + 1, length - i):  # 每次左右都要少比较一个         count_iter += 1         if nums[maxindex] < nums[j]:             maxindex = j         if nums[minindex] > nums[-j - 1]:             minindex = -j - 1     #print(maxindex,minindex)     if nums[maxindex] == nums[minindex]: # 元素相同         break     if i != maxindex:         tmp = nums[i]         nums[i] = nums[maxindex]         nums[maxindex] = tmp         count_swap += 1         # 如果最小值被交换过，要更新索引         if i == minindex or i == length + minindex:             minindex = maxindex     if minorigin != minindex:         tmp = nums[minorigin]         nums[minorigin] = nums[minindex]         nums[minindex] = tmp         count_swap += 1 print(nums, count_swap, count_iter)

3.4、等值情况优化进阶

思路：

[1, 1, 1, 1, 1, 1, 1, 1, 2]  这种情况，找到的最小值索引是-2，最大值索引8，上面的代码会交换2次，最小值两个1交换是无用功，所以，增加一个判断。

m_list = [     [1, 9, 8, 5, 6, 7, 4, 3, 2],     [1, 2, 3, 4, 5, 6, 7, 8, 9],     [9, 8, 7, 6, 5, 4, 3, 2, 1],     [1, 1, 1, 1, 1, 1, 1, 1, 1],     [1, 1, 1, 1, 1, 1, 1, 1, 2] ] nums = m_list[4] length = len(nums) print(nums) count_swap = 0 count_iter = 0 # 二元选择排序 for i in range(length // 2):     maxindex = i     minindex = -i - 1     minorigin = minindex          for j in range(i + 1, length - i):  # 每次左右都要少比较一个         count_iter += 1         if nums[maxindex] < nums[j]:             maxindex = j         if nums[minindex] > nums[-j - 1]:             minindex = -j - 1     print(maxindex,minindex)          if nums[maxindex] == nums[minindex]: # 元素相同         break              if i != maxindex:         tmp = nums[i]         nums[i] = nums[maxindex]         nums[maxindex] = tmp         count_swap += 1         # 如果最小值被交换过，要更新索引         if i == minindex or i == length + minindex:             minindex = maxindex                  # 最小值索引不同，但值相同就没有必要交换了     if minorigin != minindex and nums[minorigin] != nums[minindex]:         tmp = nums[minorigin]         nums[minorigin] = nums[minindex]         nums[minindex] = tmp         count_swap += 1          print(nums, count_swap, count_iter)

还可能存在一些特殊情况可以优化，但是都属于特例的优化了，对整个算法的提升有限。

总结

简单选择排序需要数据一轮轮比较，并在每一轮中发现极值

没有办法知道当前轮是否已经达到排序要求，但是可以知道极值是否在目标索引位置上

遍历次数1,...,n-1之和n(n-1)/2

时间复杂度O(n^2)

减少了交换次数，提高了效率，性能略好于冒泡法