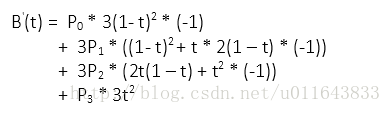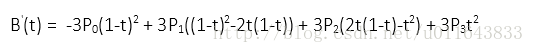写在前面

最近给项目做了个路径编辑，基本思路是满足几个基本需求：
【额外说明】其实本篇和这个没关系，可以跳过“写在前面”这部分，跨到正文部分

编辑时：
① 随意增减、插入、删除路点，只要路点数量大于1，绘制曲线，曲线必定经过路点。
② 调整路点的Forward方向，控制曲线的入线切线方向、出线切线方向。这样可以通过旋转直接调整曲线形状。
③ 控制Forward方向的基础上，增添描述切线“强度”的变量，来进一步控制曲线的形状。
④ 可以指定每段曲线的逻辑长度，程序提供一个曲线近似长度帮助确定逻辑长度。
⑤ 导出曲线的数据。

运行时，可以根绝数据：
⑥ 对路点进行从0开始的编号，使用0.01~0.99来描述在某段曲线上的位置（逻辑上的），然后转化成为实际的坐标。
⑦ 可以获得在曲线上任意一点的切线方向。

正文

从路点、路点forward到三阶贝塞尔曲线的四个点

关于贝塞尔曲线，可见下文
贝塞尔曲线
贝塞尔曲线在线演示

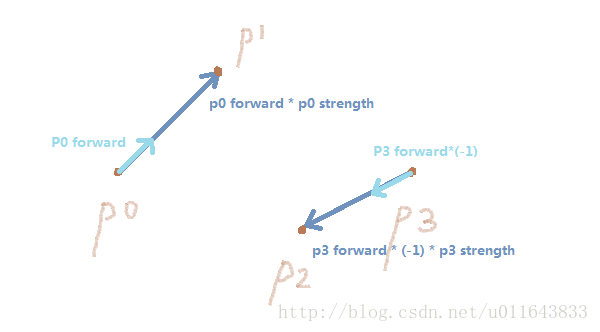
每两个路点作为三阶贝塞尔曲线的起点（第0个点P0）和终点（第3个点P3）。

起点路点的Forward方向乘以“强度”的变量，再加上起点坐标，作为第1个点P1。
起点路点的Forward反方向乘以“强度”的变量，再加上起点坐标，作为第2个点P2。

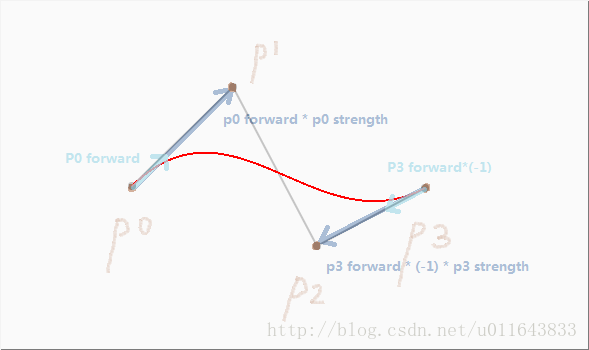
得到 p0~p4这四个点之后，即可使用三阶贝塞尔曲线的相关公式了

绘制贝塞尔曲线，图中红色线条部分

三阶贝塞尔曲线线上某点坐标（Unity & C#）

三阶贝塞尔曲线公式（来自百度百科）

形参中的 t, p0, p1, p2, p3 分别对应公式中的 t 以及 p0~p3

    public Vector3 BezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3)
    {
        float u = 1 - t;
        float tt = t * t;
        float uu = u * u;
        float uuu = uu * u;
        float ttt = tt * t;

        Vector3 p = uuu * p0;
        p += 3 * uu * t * p1;
        p += 3 * u * tt * p2;
        p += ttt * p3;

        return p;
    }

三阶贝塞尔曲线的近似长度（Unity & C#）

计算长度的思路：
在贝塞尔曲线上取n个点，计算点之间的直线长度，进行加和，从而取得一个曲线的近似长度。取点越多这个长度越趋向于精确。

形参中的p0, p1, p2, p3 分别对应公式中的 p0~p3。pointCount代表取点个数，默认30。

    public float BezierLength(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, int pointCount = 30)
    {
        if (pointCount < 2)
        {
            return 0;
        }

        //取点 默认 30个
        float length = 0.0f;
        Vector3 lastPoint = BezierPoint(0.0f / (float)pointCount, p0, p1, p2, p3);
        for (int i = 1; i <= pointCount; i++)
        {
            Vector3 point = BezierPoint((float)i/(float)pointCount, p0, p1, p2, p3);
            length += Vector3.Distance(point, lastPoint);
            lastPoint = point;
        }
        return length;
    }

三阶贝塞尔曲线线上某点的切线（Unity & C#）

在已知贝塞尔曲线表达式的情况下，想要知道某点的切线，对曲线求导。
可得：

整理后可得

整体公式构成只有p0~p3 以及 t 和 (1-t)，为了表达式更直接，不进行进一步的整理。
所以得到下面的代码

形参中的 t, p0, p1, p2, p3 分别对应公式中的 t 以及 p0~p3

    public Vector3 BezierTangent(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3)
    {
        float u = 1 - t;
        float uu = u * u;
        float tu = t * u;
        float tt = t * t;

        Vector3 P = p0 * 3 * uu * (-1.0f);
        P += p1 * 3 * (uu - 2 * tu);
        P += p2 * 3 * (2 * tu - tt);
        P += p3 * 3 * tt;        

        //返回单位向量
        return P.normalized;
    }

写在后面

主要参照：
Unity游戏中使用贝塞尔曲线
求二次、三次贝塞尔曲线的某个时间的位置及切线方向

转载请注明，出自喵喵丸的博客 （http://blog.csdn.net/u011643833/article/details/78540554）