摘要:归并排序和快速排序是两种稍微复杂的排序算法,它们用的都是分治的思想,代码都通过递归来实现,过程非常相似。理解归并排序的重点是理解递推公式和 merge() 合并函数。
本文分享自华为云社区《深入浅出八种排序算法》,作者:嵌入式视觉 。
归并排序和快速排序是两种稍微复杂的排序算法,它们用的都是分治的思想,代码都通过递归来实现,过程非常相似。理解归并排序的重点是理解递推公式和 merge() 合并函数。
一,冒泡排序(Bubble Sort)
排序算法是程序员必须了解和熟悉的一类算法,排序算法有很多种,基础的如:冒泡、插入、选择、快速、归并、计数、基数和桶排序等。
冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求,如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置,重复 n 次,就完成了 n 个数据的排序工作。
总结:如果数组有 n 个元素,最坏情况下,需要进行 n 次冒泡操作。
基础的冒泡排序算法的 C++ 代码如下:
// 将数据从小到大排序
void bubbleSort(int array[], int n){
if (n<=1) return;
for(int i=0; i<n; i++){
for(int j=0; j<n-i; j++){
if (temp > a[j+1]){
temp = array[j]
a[j] = a[j+1];
a[j+1] = temp;
}
}
}
}
实际上,以上的冒泡排序算法还可以优化,当某次冒泡操作已经不再进行数据交换时,说明数组已经达到有序,就不需要再继续执行后续的冒泡操作了。优化后的代码如下:
// 将数据从小到大排序
void bubbleSort(int array[], int n){
if (n<=1) return;
for(int i=0; i<n; i++){
// 提前退出冒泡循环发标志位
bool flag = False;
for(int j=0; j<n-i; j++){
if (temp > a[j+1]){
temp = array[j]
a[j] = a[j+1];
a[j+1] = temp;
flag = True; // 表示本次冒泡操作存在数据交换
}
}
if(!flag) break; // 没有数据交换,提交退出
}
}
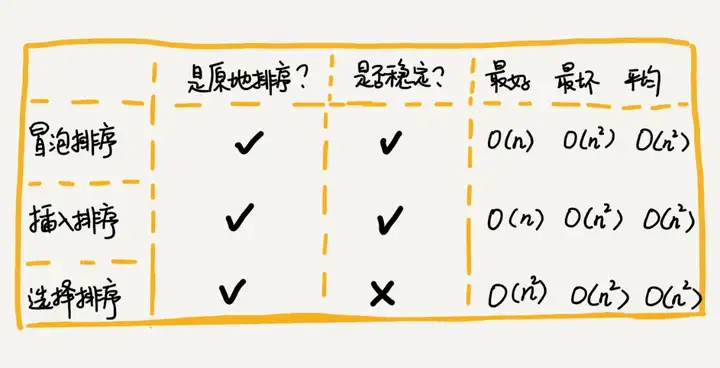
冒泡排序的特点:
- 冒泡过程只涉及相邻元素的交换,只需要常量级的临时空间,故空间复杂度为 O(1)O(1),是原地排序算法。
- 当有相邻的两个元素大小相等的时候,我们不做交换,相同大小的数据在排序前后不会改变顺序,所以是稳定排序算法。
- 最坏情况和平均时间复杂度都为 O(n2)O(n2),最好时间复杂度是 O(n)O(n)。
二,插入排序(Insertion Sort)
- 插入排序算法将数组中的数据分为两个区间:已排序区间和未排序区间。最初始的已排序区间只有一个元素,就是数组的第一个元素。
- 插入排序算法的核心思想就是取未排序区间的一个元素,在已排序区间中找到一个合适的位置插入,并保证已排序区间数据一直有序。
- 重复这个过程,直到未排序区间元素为空,则算法结束。
插入排序和冒泡排序一样,也包含两种操作,一种是元素的比较,一种是元素的移动。
当我们需要将一个数据 a 插入到已排序区间时,需要拿 a 与已排序区间的元素依次比较大小,找到合适的插入位置。找到插入点之后,我们还需要将插入点之后的元素顺序往后移动一位,这样才能腾出位置给元素 a 插入。
插入排序的 C++ 代码实现如下:
void InsertSort(int a[], int n){
if (n <= 1) return;
for (int i = 1; i < n; i++) // 未排序区间范围
{
key = a[i]; // 待排序第一个元素
int j = i - 1; // 已排序区间末尾元素
// 从尾到头查找插入点方法
while(key < a[j] && j >= 0){ // 元素比较
a[j+1] = a[j]; // 数据向后移动一位
j--;
}
a[j+1] = key; // 插入数据
}
}
插入排序的特点:
- 插入排序并不需要额外存储空间,空间复杂度是 O(1)O(1),所以插入排序也是一个原地排序算法。
- 在插入排序中,对于值相同的元素,我们可以选择将后面出现的元素,插入到前面出现元素的后面,这样就可以保持原有的前后顺序不变,所以插入排序是稳定的排序算法。
- 最坏情况和平均时间复杂度都为 O(n2)O(n2),最好时间复杂度是 O(n)O(n)。
三,选择排序(Selection Sort)
选择排序算法的实现思路有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。
选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O(n2)O(n2),是原地排序算法,且是不稳定的排序算法。
选择排序的 C++ 代码实现如下:
void SelectSort(int a[], int n){
for(int i=0; i<n; i++){
int minIndex = i;
for(int j = i;j<n;j++){
if (a[j] < a[minIndex]) minIndex = j;
}
if (minIndex != i){
temp = a[i];
a[i] = a[minIndex];
a[minIndex] = temp;
}
}
}
冒泡插入选择排序总结
这三种排序算法,实现代码都非常简单,对于小规模数据的排序,用起来非常高效。但是在大规模数据排序的时候,这个时间复杂度还是稍微有点高,所以更倾向于用时间复杂度为 O(nlogn)O(nlogn) 的排序算法。
特定算法是依赖特定的数据结构的。以上三种排序算法,都是基于数组实现的。
四,归并排序(Merge Sort)
归并排序的核心思想比较简单。如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
归并排序使用的是分治思想。分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。
分治思想和递归思想有些类似,分治算法一般用递归实现。分治是一种解决问题的处理思想,递归是一种编程技巧,这两者并不冲突。
知道了归并排序用的是分治思想,而分治思想一般用递归实现,接下来的重点就是如何用递归实现归并排序。写递归代码的技巧就是,分析问题得出递推公式,然后找到终止条件,最后将递推公式翻译成递归代码。所以,要想写出归并排序的代码,得先写出归并排序的递推公式。
递推公式:
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
终止条件:
p >= r 不用再继续分解,即区间数组元素为 1
归并排序的伪代码如下:
merge_sort(A, n){
merge_sort_c(A, 0, n-1)
}
merge_sort_c(A, p, r){
// 递归终止条件
if (p>=r) then return
// 取 p、r 中间的位置为 q
q = (p+r)/2
// 分治递归
merge_sort_c(A[p, q], p, q)
merge_sort_c(A[q+1, r], q+1, r)
// 将A[p...q]和A[q+1...r]合并为A[p...r]
merge(A[p...r], A[p...q], A[q+1...r])
}
4.1,归并排序性能分析
1,归并排序是一个稳定的排序算法。分析:伪代码中 merge_sort_c() 函数只是分解问题并没有涉及移动元素和比较大小,真正的元素比较和数据移动在 merge() 函数部分。在合并过程中保证值相同的元素合并前后的顺序不变,归并排序排序就是一个稳定的排序算法。
2,归并排序的执行效率与要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均情况,时间复杂度都是 O(nlogn)O(nlogn)。分析:不仅递归求解的问题可以写成递推公式,递归代码的时间复杂度也可以写成递推公式:
3,空间复杂度是 O(n)。分析:递归代码的空间复杂度并不能像时间复杂度那样累加。尽管算法的每次合并操作都需要申请额外的内存空间,但在合并完成之后,临时开辟的内存空间就被释放掉了。在任意时刻,CPU 只会有一个函数在执行,也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小,所以空间复杂度是 O(n)O(n)。
五,快速排序(Quicksort)
快排的思想是这样的:如果要排序数组中下标从 p 到 r 之间的一组数据,我们选择 p 到 r 之间的任意一个数据作为 pivot(分区点)。我们遍历 p 到 r 之间的数据,将小于 pivot 的放到左边,将大于 pivot 的放到右边,将 pivot 放到中间。经过这一步骤之后,数组 p 到 r 之间的数据就被分成了三个部分,前面 p 到 q-1 之间都是小于 pivot 的,中间是 pivot,后面的 q+1 到 r 之间是大于 pivot 的。
根据分治、递归的处理思想,我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据,直到区间缩小为 1,就说明所有的数据都有序了。
递推公式如下:
递推公式:
quick_sort(p,r) = quick_sort(p, q-1) + quick_sort(q, r)
终止条件:
p >= r
归并排序和快速排序总结
归并排序和快速排序是两种稍微复杂的排序算法,它们用的都是分治的思想,代码都通过递归来实现,过程非常相似。理解归并排序的重点是理解递推公式和 merge() 合并函数。同理,理解快排的重点也是理解递推公式,还有 partition() 分区函数。
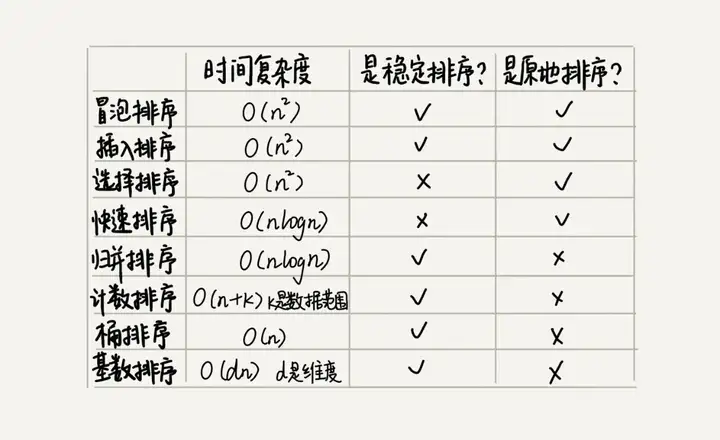
除了以上 5 种排序算法,还有 3 种时间复杂度是 O(n)O(n) 的线性排序算法:桶排序、计数排序、基数排序。这八种排序算法性能总结如下图:
参考资料
- 排序(上):为什么插入排序比冒泡排序更受欢迎?
- 排序(下):如何用快排思想在O(n)内查找第K大元素?
点击关注,第一时间了解华为云新鲜技术~